从Happy num所想到的几个问题

首先，前几天在leetcode上刷到了一题，做的时候边发现这个难度为easy的题目实际上是非常有意思的。先把题目放上来：

【题目翻译】我们把满足如下性质的自然数$n$称为快乐数：以19为例，若$1^2+9^2=81→8^2+1^2=68→6^2+8^2=100→1^2+0^2+0^2=1$，即最后收敛到1的数称为快乐数。那么请判断一个自然数$n$是否为快乐数。

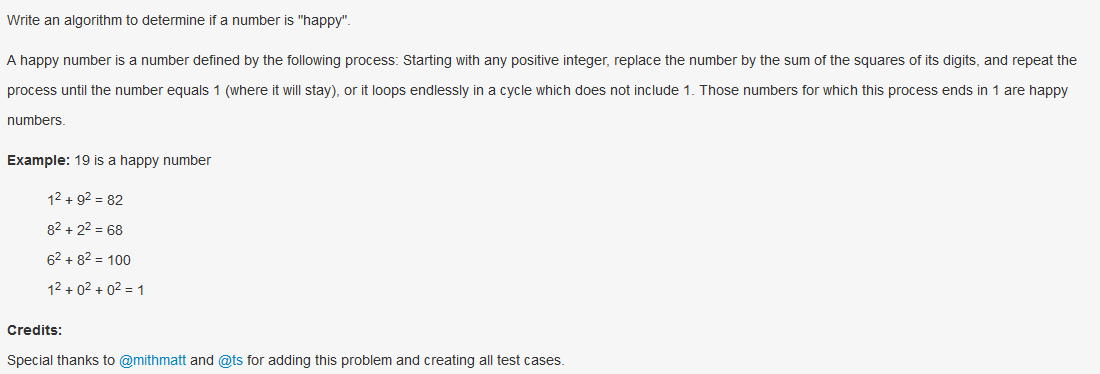
以224为例可以把这样的操作可视化如下：

这个问题困难在于如何判断程序的停止，包括我在AC之后，查看discuss以及各种CSDN，都没有对这个问题的完美数学解释，即为何：若一个数n不为happy number，那么它将会进入4-循环，即：

4→16→37→58→89→145→42→20→4

结合维基百科，下面先给出一个不是满意的证明。之所以说不满意是因为，有一步需要用计算机编程检验，而不能从纯数论的角度出发证明╮(╯▽╰)╭。

关于happy num终止条件的数学证明

命题：任取一个自然数n，若n不为happy number 那么必会进入4-循环。
证明：我们用先做如下定义，设$n=\overline{a_1a_2...a_m}$，那么令$S(n)=\sum_{i=1}^ma_m^2$，其中$a_i \in \{0,1,2...,9\}$。

$(1)$首先先考察$1000 \leq n$的情况，显然有：

$$S(n)=S(\overline{a_1a_2...a_m}） \leq m \cdot9^2=81m$$
另外由于现在考察的是 $1000 \leq n$的情况，所以有：
$$n>10^{m-1}>81m$$
由上述两式，知道 $1000 \leq n$时有： $S(n)\leq n$，即为递减函数，对任意的大于1000的自然数 $n$，必存在一个自然数$t$，使得对 $n$作用$t$次 $S(x)$后必会小于1000。由于 $S(x)$是递减函数，而且有下确界1000，那么 $n$必会收敛到1000，而此时$S(1000)=1$为快乐数。所以，只需要考虑 $n\leq 999$的情况即可。

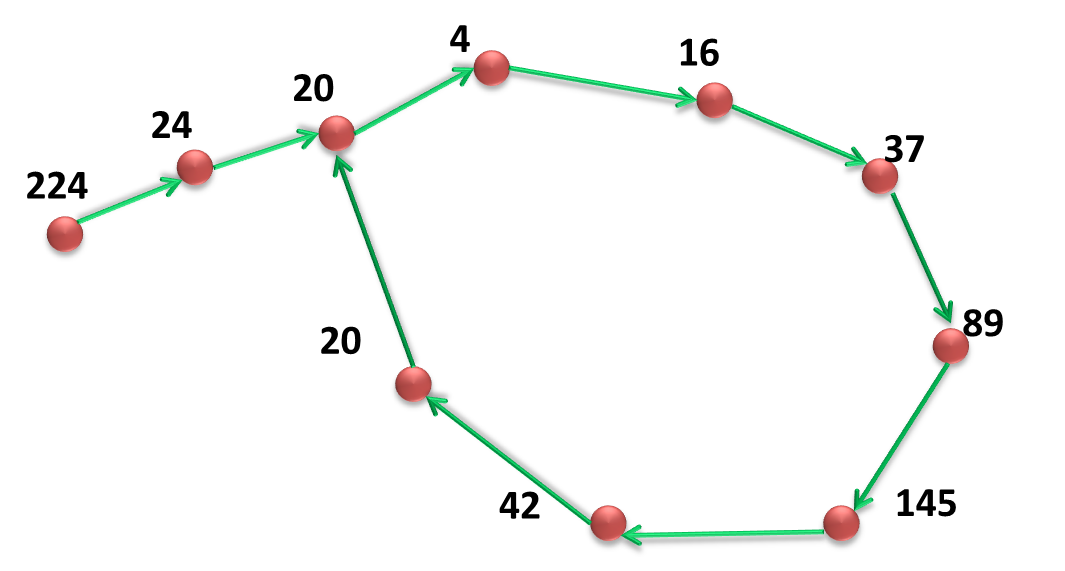
$(2)$当$n\leq 99$时可以用计算机枚举证明，若不为快乐数，那么必会进入4-循环。TAT不开心根本想不出纯数论的证明，感觉和$3x+1$猜想差不多。如图为，几个测试的数，可以看到最终都会进入4-循环，好神奇。

$(3)$当然有的童鞋说直接把小于1000的都检验不就完了吗，确实如此，不过这里还是可以看看其数学内涵的。假设$S(n)>100$（否则由上分析若小于100那么已经可以证明了）考察区间[100,999]中的自然数$n$，已知$supS(n)=S(999)=243$，于是对$n \in [100,999]$，$S(n) \in [100,243]$，同样得[100,243]中$supS(n)=107$…于是我们可以得到类似于$1000 \leq n$的递减区间（闭区间套？！）

$$[100,100]\subset[100,101]\subset...\subset[100,107]\subset[100,243]\subset[100,999]$$
即若不进入二位数，则必会收敛到一个快乐数100。

综上所述，命题得证。$\square$

成环操作次数是无上界的

感谢蔡神提出一个问题，这样的成环操作次数会不会有上界呢？
这是一个好问题，假设有上界那么我就称之为蔡爷常数吧~液
然而，5555，貌似构造出来了。
虽然从图2中，其实收敛速度是超级快的，但是却没有上界，这是因为任取一个数$k_0$，假设需要操作$t$次，那么构造$k_1=111...111$，一共$k_0$个1，那么$k_1$的操作次数为$t+1$次，类似得构造$k_2,k_3,...$，便可知道操作次数没有上界。

关于happy num的程序

于是乎有了上述的讨论，就阔以安心得下出如下代码噜：

int count_square(int k)
{
    int size=(int)(log10(k))+1;
    int a[size];
    int sum=0;
    for(int i=0;i<size;++i){
            a[i]=k%10;
            k=(k-a[i])/10;
            sum=sum+a[i]*a[i];
        }
        return sum;
}
bool isHappy(int n) {
    if(n==0)
        return 0;

    while(1){
     int judge=count_square(n);
       if(judge==1)
         return 1;
       if(judge==4)//快乐数一定会进入4循环
         return 0;
       else
         n=judge;
    }//printf("%d\n",judge);
}

一种特别的想法

但我查看OJ的discuss时看到了一个有趣的算法，比如实际上在上面写程序的时候，实际上相当于是一种hash table的思想，即存储所有的结点，然后一旦出现重复结点（如4等）那么程序就终止。然而这里将给出一个神奇的想法。另外这个算法被称为：
Floyd’s Cycle Detection Algorithm

这是一个在图论中判断一个有向图是否成环的算法。

Floyd’s Cycle算法描述

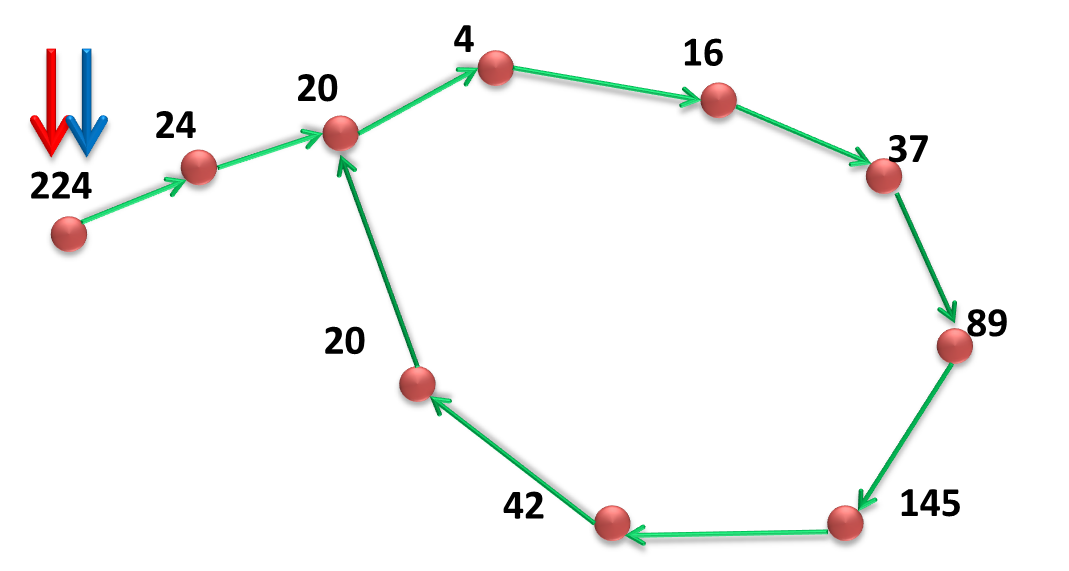
如图所示，现有两种颜色的指针，设红色的指针的速度为1，蓝色的指针速度为2，即下一个步骤红色将指到24，蓝色指到20。若出起点外，红蓝指针在某一个时刻相遇那么说明有向图中有环。

Floyd’s Cycle算法的简单证明

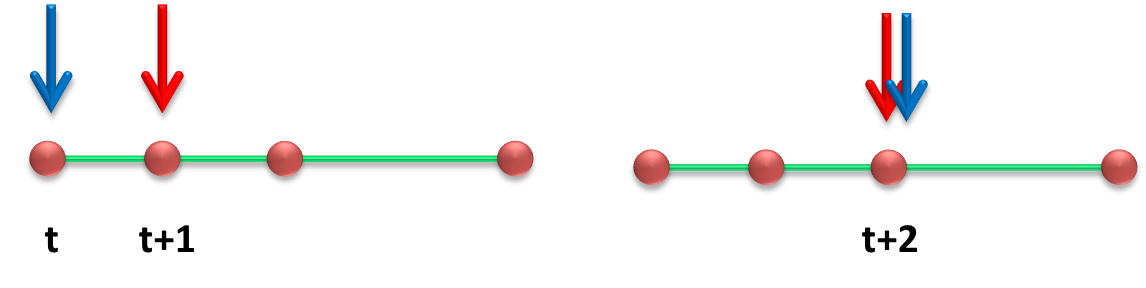
若有向图有环，那么一般地设此时蓝色指针的地址为$t_0$，红色指针所在的位置为$t_0+k$（图中的$k=1$），那么$p$次移动之后，蓝色指针所在的位置为$t_0+2p$，红色指针所在的位置为$t_0+k+p$，令$t_0+2p=t_0+k+p$，显然有解$p=k$，即$k$次操作之后红蓝指针即会相遇。（自古红蓝出CP）

Floyd’s Cycle环入口的确定

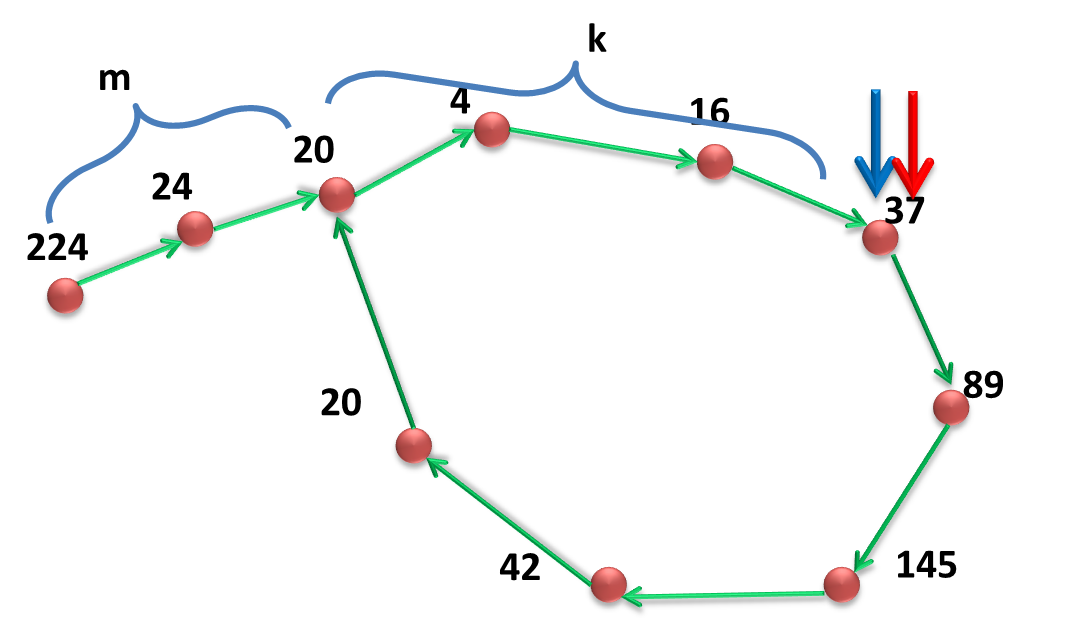
如图所示，设起点到环入口起点的距离为$m$，环起点到第一次相遇的地方距离设为$k$，设环的长度为$n$，不妨设蓝色的指针走了$I$步，红色指针走了$2I$步，那么有：

$$\begin{array}{l} I{\rm{ = }}m + an + k\\ 2I = m + bn + k \end{array}$$
其中 $a,b \in N$,两式相减得到 $I=(b-a)n$，即实际上蓝色指针走过的路程恰好为环周长的整数倍。此时只需要将其中一个指针放回最开始的起点，假设此时两个指针都变成蓝色，那么当放回起点的指针走了 $m$步的时候，另一个指针相当于从起点走了$m+I$步，且在环的起点相遇。简单地说，即首先让红蓝指针各走各路，记录第一次相遇的点的位置，然后取两个蓝色指针一个在起点一个在相遇点，那么这两个蓝色指针首次相遇的地方即为环的起点！
于是就可以利用这个原理写出如下代码：

class Solution {
public:
    bool isHappy(int n){
        int low=n,fast=n;
        while(1)
        {
            int temp=0;
            while(low)
            {
                int l=low%10;
                temp+=l*l;
                low/=10;
            }
            low=temp;
            temp=0;
            while(fast)
            {
                int f=fast%10;
                temp+=f*f;
                fast/=10;
            }
            fast=temp;
            temp=0;
            while(fast)
            {
                int f=fast%10;
                temp+=f*f;
                fast/=10;
            }
            fast=temp;
            if(low==1 || fast==1) return true;
            if(fast==low) return false;
        }
    }
};

一个神奇的延伸

Pollard’s rho 算法

前方高エネルギー非戦闘員は速やかに待避せよ

当我浏览Cycle detection的英文维基页面的时候，手贱得点了日文版页面Σ(ﾟДﾟ)。然后一个神奇的东西吸引了我：

关键词即：【フロイドの循環検出法】→【擬似乱数列を使った素因数分解】。简单得说就是这检测有向图是否成环的算法居然和。。居然和自然数的素因子分解有关！！！Σ(ﾟДﾟ)
另外英文对应的算法称为：
Pollard’s rho algorithm
此处不再赘述。维基即可，另外提供作者原论文以及改进版论文。《算法导论》P550-P552也有详细描述。
这是一个神一般的神算法，属于启发式算法，有很多即使看了原论文也不懂的地方，比如为什么要用$(x^2+a)mod \quad n$作为随机函数？！why?!然而就是这么神奇Σ(ﾟДﾟ)。

dede 素因子分解算法

当然，这种方法显然没有上面的分解算法流弊。上次想到了一个素因子分解算法。蛮暴力的思路，然而证明了分解效率是很低下的。先描述一下先：
设$n=\overline{a_1a_2...a_m}$，那么我们可以将自然数$n$随机分割为$k$个部分，比如当$k=2$时，可以这样拆分：$n=\overline{a_1a_2..a_t}\times10^{t-1}+\overline{a_{t+1}a_{t+2}..a_m}$，实际上只需要$gcd(\overline{a_1a_2..a_t},\overline{a_{t+1}a_{t+2}..a_m})>1$，既可以分解成功。下面从两个方面说明这样的算法几乎是要跪的：

从分割效率上看

一个自然数$n=\overline{a_1a_2...a_m}$要分成$k$份，实际上就相当于现在排着有顺序的$m$个球，在$m$个球中插入$k-1$个隔板的操作，这是经典的隔板法。操作数为$\binom{m-1}{k-1}$，复杂度大约是$O(n^{k-1})$，这是一个可怕的复杂度，可能只有$k=2,3$的时候还是可以接受的。

从互素效率上看

实际上，让$k$个数进行求最大公约数运算($gcd$)的话，是非常难成功的，先看如下定理：任取两个自然数，它们互素的概率为$\frac{1}{\zeta(2)}=\frac{6}{\pi^2}\approx0.6079$，其中$\zeta(n)$为黎曼$zeta$函数。类似地，任取$k$个自然数，它们互素的概率为$\frac{1}{\zeta(k)}$，然而当$k=4$的时候已经为0.99..了。囧看来不能分解成太多部分，否则几乎是不可能求得素因子的，另外$k=3$的时候，互素概率达到80%以上。综上，这不是一个好算法，好吧，分解成两部分还是可以尝试的╮(╯▽╰)╭。