过拟合、正则化点点滴滴

过拟合、正则化点点滴滴

文档可下载

1. 判断方法

过拟合（Over-fitting），模型在训练样本表现的过于优越，在验证集和测试集表现不佳。出现这种现象的原因是训练数据中存在噪音或者训练数据太少。

过拟合问题，特征维度（或参数）过多，导致拟合的函数完美的经过训练集，但是对新数据的预测结果较差。

2.产生的原因

造成过拟合的原因可以归结为：参数过多  或  样本过少

常见的原因：

1. 训练样本数据量太少、样本标注错误
2. 样本噪音干扰过大，使得机器将部分噪音认为是特征从而扰乱了预设的分类规则
3. 参数太多，模型复杂度过高
4. 权值学习迭代次数足够多（Overtraining）即训练轮数过大，拟合了训练数据中的噪音和训练样例中没有代表性的特征。

3. 解决方法|防止过拟合

1. 在神经网络模型中，可使用权值衰减（L2）的方法，即每次迭代过程中以某个小因子降低每个权值。
2. Early stopping：选取合适的停止训练标准，使对机器的训练在合适的程度
3. 数据增强
4. 正则化，L1和L2正则化、Dropout随机选取正则化。

4. 为什么正则化能解决过拟合？

特征变量过多会导致过拟合，为了防止过拟合会选择一些比较重要的特征变量，删掉很多次要的特征变量，但是我们希望利用这些特征信息，所以添加正则化来约束这些特征变量，使得这些特征变量的权重很小，接近0，这样就能保留这些特征变量，又不至于使得这些特征变量的影响过大。

5. L1和L2正则化？

L2和L1范数正则化都有助于降低过拟合风险，但是L1还会带来一个额外的好处，L1正则化更易获得“稀疏”解，即它求得的参数W会有更少的非零分量。

6. L1为什么更能容易得到稀疏解？

假定特征集合x两个特征，x={x1,x2}。对应的W也有两个分量即w={W1,W2}。然后分别再2维坐标上绘制出损失函数的等值线(即在（W_1,W_2）空间中平方误差项值相同的点的连线)。然后分别绘制出L1范数和L2范数的等值线。如下图所示：

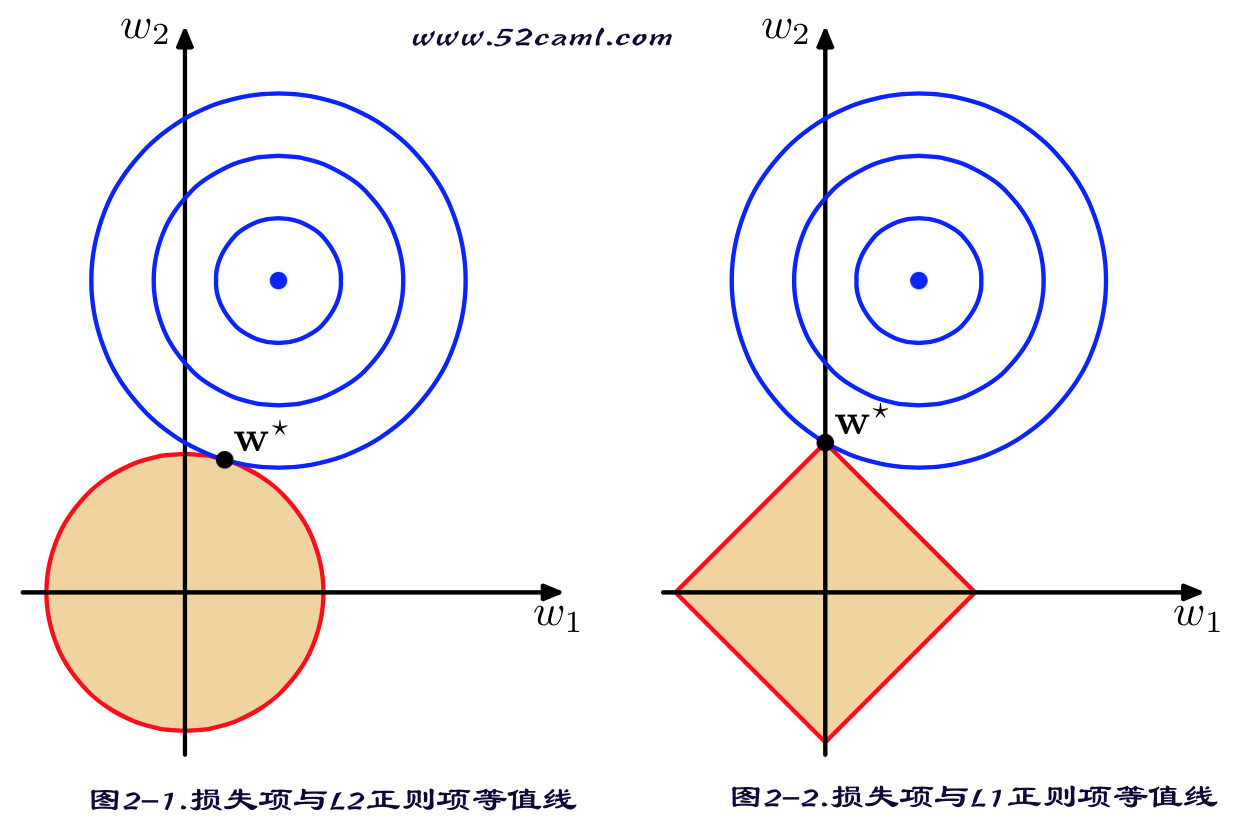
带正则化项求得的解w要在损失函数项和正则化项之间这种，即出现在图中损失函数项等值线与正则化项等值线相交处。从图2-2可以看出，采用L1范数时平方损失项的等值线与正则化项等值线的交点出现在（参数空间）坐标轴上，即w1或w2为0；而在采用L2范数时，两个等值线的相交点常出现在某个象限内（如图示第2象限），即w1或w2均非0。从图示例可以看出，在目标函数中，加入采用L1范数比L2范数更易于得到稀疏解。

7. L1和L2正则化的区别？