公路村村通（浙大PTA数据结构与算法题目集-编程题7-10）

· 题目内容

现有村落间道路的统计数据表中，列出了有可能建设成标准公路的若干条道路的成本，求使每个村落都有公路连通所需要的最低成本。

输入格式:

输入数据包括城镇数目正整数N（≤1000）和候选道路数目M（≤3N）；随后的M行对应M条道路，每行给出3个正整数，分别是该条道路直接连通的两个城镇的编号以及该道路改建的预算成本。为简单起见，城镇从1到N编号。

输出格式:

输出村村通需要的最低成本。如果输入数据不足以保证畅通，则输出−1，表示需要建设更多公路。

输入样例:

6 15
1 2 5
1 3 3
1 4 7
1 5 4
1 6 2
2 3 4
2 4 6
2 5 2
2 6 6
3 4 6
3 5 1
3 6 1
4 5 10
4 6 8
5 6 3

输出样例:

12

· 题目解析 

题目理解起来没什么难度，就是一道比较板子的最小生成树（MST）题目。用Prim或者Kruskal都可以。

Prim算法

算法基本思路和原理也比较容易理解。从任意一个顶点开始，每次将一个到该生成树权值最小的顶点纳入生成树（也即在生成树所有邻接到的顶点中选择权重最小的一个）。和Dijkstra一样，采用的是贪心策略。

至于Prim算法为什么得到的一定是最小生成树的严格证明，可以参考算法导论。其实直观上、感性上很好理解这个算法为什么得到的就是MST，每次连通一个点，而且每次还选的是边权最小的顶点，当所有顶点连通时必然是一个最小生成树。这里主要是记一下Prim实现代码里一些当时一下子没转过弯来的点。

先上代码，转自 最小生成树（MST）（最小连通子图）（算法笔记）

int prim(int s){
	fill(d , d + MAXN , INF);
	d[s] = 0;
	int ans = 0;
	for(int i = 0; i < n; i++){    // 最小生成树n个顶点，需要循环n次
		int u = -1 , MIN = INF;
		for(int j = 0; j < n; j++)    // 在还没加入到生成树的顶点中找距离MST最近的顶点Vmin
			if(hashTable[j] == false && d[j] < MIN){
				u = j;
				MIN = d[j];
			}
		if(u == -1) return -1;    // 原图不连通的处理
		hashTable[u] = true;    // 把Vmin加入MST
		ans += d[u];            // 更新总的边权
        // 由于Vmin被加入生成树，所有Vmin邻接的点到MST的最短距离都会受到影响，需要更新
		for(int j = 0; j < Adj[u].size(); j++){    
			int v = Adj[u][j].v;
			if(hashTable[v] == false && Adj[u][j].w < d[v])
				d[v] = Adj[u][j].w; 
		}
	}
	return ans;
}

第一个点是这里的数组d[]，虽然Prim算法看起来和Dijkstra有十分甚至九分相像，但这个d[]的作用差的很大，Prim的d[]存放的是到某顶点Vi到已经建立的最小生成树最短距离

第二个点是不连通情况的处理。第二个for循环处会在所有还没加入到生成树的顶点中找到MST最近的顶点。如果有顶点不连通的话，它到图中其他顶点距离是∞，那么处理到最后，总会剩下这个顶点。此时由于在for循环前已经把u初始化为-1，经过for循环后，u还是-1没有被更新为到MST最近的顶点编号，直接返回-1表示该图不连通。

第三个是d[]数组的更新。这个比较好理解，每次将边权最小的顶点加入生成树，生成树所包含的顶点就变了，其他顶点到最小生成树的距离也可能因此改变。但不是全部顶点都会变，受影响的只有加入的顶点（Vmin）邻接到的那些顶点。如果到Vmin的距离比原来的最短距离短，就更新d[]。

Kruskal算法

Kruskal算法要用到一个数据结构叫做并查集。因为Kruskal算法是每次选取一条权重最小的边，若该边连接的两个顶点不连通，则保留该边，并通过该边将其两端的顶点连通；否则丢弃这条边这条边。这样在处理的时候，每次得到的并不一定是连通的树，而可能是连通森林。所以要用到并查集来表示。比如这个图，最开始应该选择边权为1的那条连接P城、学校的边，之后应选择边权为2，连接矿场、渔村的边。这样产生的是一个是一个生成森林。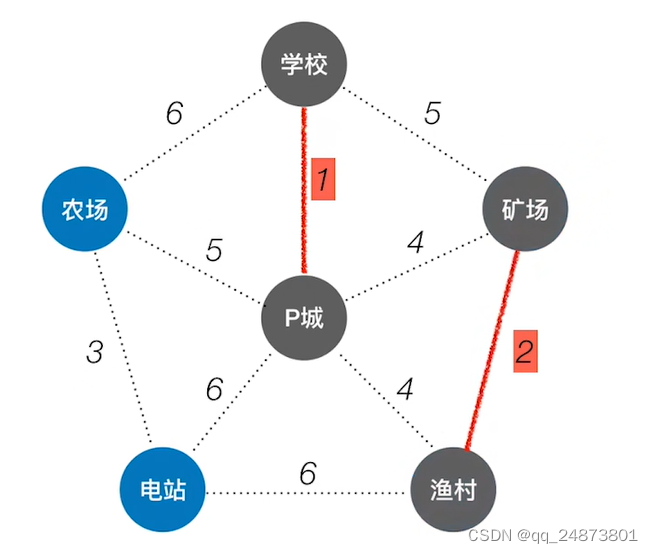

并查集的原理和实现也比较简单。需要一个数组parent，存放某个结点的父结点编号。最开始时这个把这个数组所有元素初始化为元素下标，表示该结点是一个根结点，父结点是其本身，也就是每个结点自己单独作为一个集合。

并查集有两个基本操作：“查”和“并”。

查（Find）是寻找某个结点所属集合，每次判断该结点父结点编号parent[x]与结点下标x，如果不相等，则跳至父结点（x=parent[x]）直至相等，此时说明已到达根结点。根结点编号可看作是该结点所属集合。

并（Union）是将两个并查集合并为一个。首先通过Find找到两个结点x,y所在树的根结点，如果相同证明x,y处于同一个并查集。否则将其中一棵树挂到另外一个结点上（给其中一棵树的根的父结点赋值为另一棵树的根结点编号）。

Kruskal算法在执行时，首先将边按权值递增排序，随后依次遍历所有边，判断其所连接的两个顶点是否属于同一并查集，如果不是，说明二者属于不同的连通子树，则将其合并到同一并查集并更新总权值。所有边都执行完毕后，依次判断所有结点的并查集，如果有某个结点所属的并查集不同，说明原图是不连通的，返回-1。

代码如下：

int Kruskal(Graph G) {
    int Vnum = G->VexNum, Enum = G->EdgeNum;    // 顶点数、边数
    int res = 0;
    int start,end,weight;  // 存放边的起点、终点、边权
    int parent[Vnum+1];
    // 初始化并查集各结点所在集合为自身
    for(int i=0;i<Vnum+1;i++)
        parent[i] = i;
    // 将边按边权排序
    for(int i=0;i<Enum;i++) {
        for(int j=0;j<Enum-1;j++) {
            if(G->edges[j]->weight>G->edges[j+1]->weight) {
                Edge tmp = G->edges[j];
                G->edges[j] = G->edges[j+1];
                G->edges[j+1] = tmp;
            }
        }
    }
    // 按边权递增顺序将边加入生成树
    for(int i=0;i<Enum;i++) {
        start = G->edges[i]->start;
        end = G->edges[i]->end;
        weight = G->edges[i]->weight;
        while(start!=parent[start])  {
            start = parent[start];  // 找start所属并查集
        }
        while(end!=parent[end])  {
            end = parent[end];      // 找end所属并查集
        }
        if(start!=end) {    //start end所属并查集不同，说明不属于同一个连通森林
            // 将其合并至同一连通森林
            parent[end] = start;
            res += weight;
        }
    }

    for(int i=1;i<Vnum;i++)  {
        int x=i,y=i+1;
        while(x!=parent[x])  {
            x = parent[x];  // 找i所属并查集
        }
        while(y!=parent[end])  {
            y = parent[y];  // 找i+1所属并查集
        }
        // 若连通，所有顶点都应在同一个并查集。否则不连通，返回-1
        if(x!=y) return -1;
    }
    return res;
}

算法的比较

对于Prim算法，把所有顶点纳入最小生成树的时间复杂度是O(|V|)，每次纳入顶点时，需要进行两个操作：遍历所有顶点找到一个距MST最近的顶点、遍历该顶点所有边更新d[]，总体时间复杂度为O(|V|²)。适用于边稠密图

对于Kruskal算法，总共有这样几个操作并行：初始化顶点父结点数组parent（O(|V|)）,按边权递增排序（快排O(|E|log|E|)，冒泡等O(|E|²)），将边按递增顺序加入生成树O（(|E|)），判断连通（O(|V|)），总体时间复杂度与排序方法有关O(|E|log|E|)~O(|E|²)，适用于边稀疏图。

在PTA上我用的Prim是可以通过所有检查点的，用冒泡排序的Kruskal会超时。

（扯句题外话，假设最开始没有这个算法的时候，我想大多数人拿到一个图要找最小生成树，可能想到的都是做“减法”，也就是怎么在众多的边当中删繁就简去掉冗余的权值大的边，只剩下权值小的边。但是Prim和克鲁斯卡尔算法都是反其道行之做“加法”，从0开始一步步把符合的东西加上去，最后得到结果，可能这就是“生成”两字的由来吧）