GDOI2016模拟8.16帮派

农场里的生活很艰苦，而且当生活很艰苦，你必须坚强起来。奶牛们形成了编号为1到M的帮派。这些帮派一开始和睦相处了一段时间，但是现在失控了！

奶牛们在竞争一片大草地的控制权。奶牛之间的冲突发生在连续的若干分钟内。每一分钟有一只奶牛走进草地。如果此时草地上没有奶牛，那么这只新进去的奶牛所在的帮派就能占领这片草地。如果草地上已经被新进去的奶牛的帮派所占领了，那么这只奶牛就在草地里吃草。否则，一只属于正在占领草地的帮派的奶牛会跟新来的奶牛发生冲突。

这些发生在两只奶牛之间的冲突由吵架开始，然后两只奶牛就会发现他们的共同点比他们的不同点更多。然后两只奶牛发现他们各自的错误，就离开他们所在的帮派，走出草地，再去FJ的客栈里喝一杯冷牛奶。如果在某次冲突之后，草地里没有奶牛，那么没有帮派占领草地。

Bessie知道这些冲突是怎么发生的。她知道每一个帮派有几只奶牛。Bessie很想在所有冲突都发生完，每只奶牛要么在草地上，要么在FJ客栈里之后，让她所在的帮派占领这片草地。请你帮助Bessie判断她所在的帮派（编号为1）是否有可能占领草地。

如果有可能占领草地，Bessie想知道最后最多能有多少只奶牛是属于她所在的帮派的。输出这个数字和能让Bessie的帮派占领草地的字典序最小的方案（每分钟进入草地的奶牛的帮派编号的序列）。一个序列X字典序比序列Y小的意思是有某个k,X[k]

这题一开始就没有好的想法，考的时候就弃疗了…
而且没给部分分范围。。。。

现在假设我们我们不必要求字典序，若给定前面一部分已经选择的序列，我们要使得后面能有一种方案使得留下的1最多，那么我们可以这样放：
首先，剩余1肯定在最后，中间的（不包含1）可以这样放：
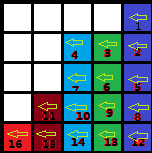
先按数量从小到大排，按如下（柱状图）放，箭头表示选取方向：

我们可以发现，这样选取的特点，若展开成一个序列，那么相邻的可以互相抵消，同时，它也是能使前面选择不管是什么序列，都可以尽可能将帮派消掉，这样，我们可以得到一个最优方案来判断，当前选择的序列（前面的），能否满足答案，剩下的，只需要枚举答案，让后枚举前面的序列，判断是否合法就行了。
时间复杂度：O（$N^{2}MlogN$）
贴代码：

#include<iostream>
#include<cstdio>
#include<algorithm>
using namespace std;
#define N 102
int n,m,ans;
int a[N],b[N],d[N];
bool p;
struct node{
    int x,y;
}c[N];
void init(){
    scanf("%d %d",&n,&m);
    for (int i=1;i<=m;i++)
        scanf("%d",&a[i]);
}
bool cmp(const node&a,const node&b){
    return a.y<b.y;
}
bool get(){
    static int sum,xx,yy;
    sum=0;
    for (int i=2;i<=m;i++)
        if (b[i]){
            c[++sum].x=i;
            c[sum].y=b[i];
        }
    sort(c+1,c+sum+1,cmp);
    xx=sum;
    for (;c[1].y;){
        if (c[xx].y>c[xx+1].y){
            d[++d[0]]=c[xx].x;
            c[xx].y--;
            xx--;
        }else{
            d[++d[0]]=c[sum].x;
            c[sum].y--;
            xx=sum-1;
        }
    }
    while (d[0]!=n)d[++d[0]]=1;
    xx=0,yy=0;
    for (int i=1;i<=n;i++)
        if (!yy||xx==d[i]){
            yy++,xx=d[i];
        }else
            yy--;
    return (xx==1)&&(yy==ans);
}
bool jian(){
    static bool p;
    for (int i=1;i<=m;i++)
        b[i]=a[i];
    for (int i=1;i<=n;i++){
        p=0;
        for (int j=1;j<=m;j++)
            if (b[j]){
                d[0]=i;
                --b[j];
                d[i]=j;
                if (get()){
                    p=1;
                    break;
                }
                ++b[j];
            }
        if (!p)return 0;
    }
    return 1;
}
void work(){
    for (ans=a[1];ans;ans--)
        if (jian()){
            p=1;
            return;
        }
}
void write(){
    if (!p)printf("NO");
    else{
        printf("YES\n");
        printf("%d\n",ans);
        for (int i=1;i<=n;i++)
            printf("%d\n",d[i]);
    }
}
int main(){
    init();
    work();
    write();
    return 0;
}