时间复杂度和空间复杂度的分析

时间复杂度

本质就是在计算基本操作重复执行的次数 ，并且大多数情况下分析的是最坏情况的，通常用O()来表示

计算的时候两个准则：

1.忽略掉那些常数

2.关注函数式中增长最快的表达式

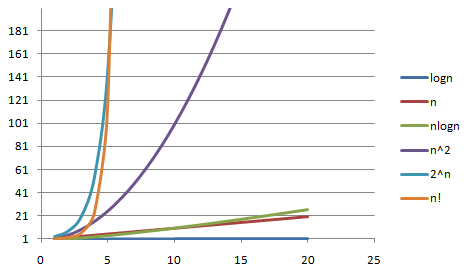
常用的时间复杂度有以下几种，算法时间复杂度依次增加：O(1)常数型、O(log2 n)对数型、O(n)线性、O(nlog2 n)二维型、O(n^2)平方型、O(n^3)立方型、O(2^n)指数型、通过下图我们感受下这几种时间复杂度的差异

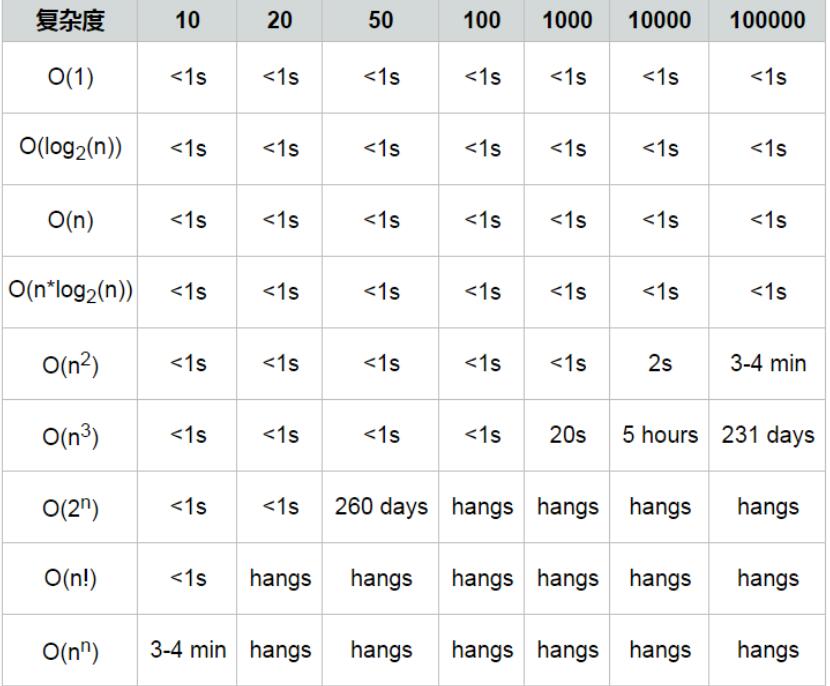
在这里我们为了更加直观感受高效程序和低效程序的差别再来分享一张表

由上图我们可以看出时间复杂度越大，程序的效率越低，并且在二维型以下时间复杂度差距不是很大，可见程序的时间复杂度

在二维型以下都是比较高效的

空间复杂度

计算整个算法的辅助空间单元的个数，并不是计算实际占用的空间，辅助空间指的是为局部变量和形参所开辟的空间

示例

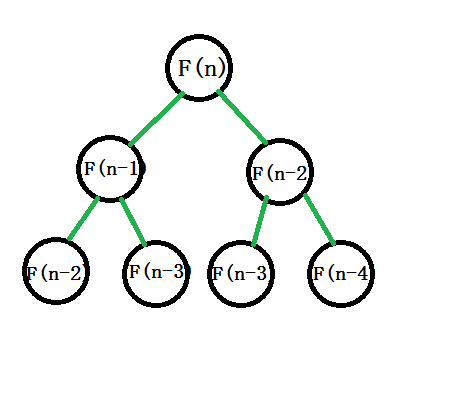
斐波那契数列递归算法时间复杂度

    long long Fib(int n)  
    {  
           assert(n >= 0);  
           return n<2 ? n : Fib(n - 1) + Fib(n-2);  
    }  

递归算法的时间复杂度是：递归次数*每次递归中执行基本操作的次数
递归算法的空间复杂度是：递归的深度*每次压栈所需的空间个数
递归有运行时堆栈，求的是递归最深的那一次压栈所耗费的空间的个数

时间复杂度：O(2^N)  【深度是n,节点个数就是2^n】

空间复杂度：O(N)

斐波那契数列非递归算法时间复杂度

    long long *Fib(int  n)  
    {  
           assert(n>=0);  
           long long *array = new long long[n + 1];  
           array[0] = 0;  
           if (n > 0)  
           {  
                  array[1] = 1;  
           }  
           for (int i = 2; i <n+1; i++)  
           {  
                  array[i] = array[i - 1] + array[i - 2];  
           }  
           return array;  
    }  

时间复杂度：O(N)

空间复杂度：O(N)