排列与组合
概念
- 研究离散数学的排列组合的问题,对离散对象的计数
(1)研究三大问题:存在性,计数性,优化性- 加法法则与乘法法则
(1)加法法则:分类问题(A->B: 火车3趟,客车2趟;男20,女10;)
(2)乘法法则:分步问题(A->B->C: A->B火车3趟,B->C客车2趟)- 减法法则
(1)定义A的补集 A ‾ \overline{A} A:A = S - A ‾ \overline{A} A
(2)一一对应:计数时常用技巧,A容易,B困难,A与B一一对应,对B的计数转为A。
- A 表示集合,| A | 表示集合的个数 m,| B | 个数 n
(1)| A * B | = m * n- 排列和组合
(1)组合:不考虑顺序,称为组合数 C(4,3) = 4! / 3!
(2)排列:考虑顺序,称为排列数 P(4,3) = 4 * 3 * 2,P(n,r) = n! / (n-r)!- 排列的递推关系
(1)分布递推(选第一个盒子内的乒乓球,其它)
[1] P(n,r) = n P(n-1, r-1)
(2)分类递推(选第一个球,不选第一个球)
[1] P(n,r) = P(n-1, r) + r P(n-1, r-1)- 组合的递推:C(n,r) * r! = P(n,r) = n! / (n-r)!
(1) C(n,r) = C(n,n-r)
(2) C(n,l) C(l,r) = C(n,r) C(n-r,l-r)- Cayley定理:过n个有标志顶点的树的数目等于nn-2
- 组合恒等式
(1) C(m+n,r) = C(m,0)C(n,r) + C(m,1)C(n,r-1) + … + C(m,r)C(n,0)
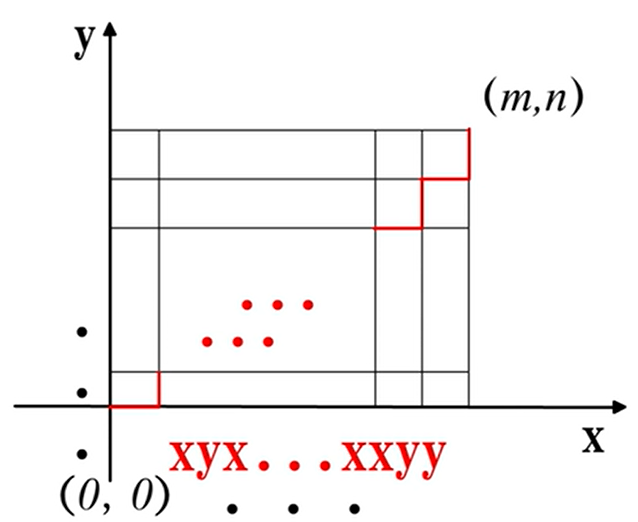
[1] 理解为:红m蓝n球,共抽出 r 个球- 格路模型:C(m+n, n)


























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








