XGB算法梳理-CSDN博客

本文链接：https://blog.csdn.net/qq_25614773/article/details/89185218

【3】XGB算法梳理

文章目录

【3】XGB算法梳理

1.算法原理

xgboost的基础是梯度提升算法，提升法中最著名的算法包括Adaboost和梯度提升树，xgboost是由梯度提升树GBDT发展而来。梯度提升树可以有回归树和分类树，两者都是以CART树算法为主流，xgboost背后也是CART树，这意味着xgboost中所有树都是二叉树。

1.1.核心公式推导

目标函数
$J(f_t)=\sum_{i=1}^nL(y_i,\hat{y}_i^{(t-1)}+f_t(x_i))+\Omega(f_t)+C$
根据Taylor展开式：

$f(x+\Delta x)\approx f(x)+\nabla f(x)\Delta x+\frac{1}{2}\nabla^2 f(x)\Delta x^2$

令
$g_i ==\frac{\partial L(y_i,\hat{y}_i^{(t-1)}) }{\partial \hat{y}_i^{(t-1)}}$

$h_i ==\frac{\partial^2 L(y_i,\hat{y}_i^{(t-1)}) }{\partial^2 \hat{y}_i^{(t-1)}}$

$J(f_t)=\sum_{i=1}^n[L(y_i,\hat{y}_i^{(t-1)})+g_if_t(x_i)+\frac{1}{2}h_if_i^2(x_i)]+\Omega(f_t)+C$

正则化定义：

决策树的复杂度可考虑叶节点树和叶权值

$\Omega(f_t)=\gamma T+ \frac{1}{2}\lambda\sum_{i=1}^T\ W_j^2$

目标函数计算
$\begin{aligned} J(f_t) &\approx \sum_{i=1}^n[L(y_i,\hat{y}_i^{(t-1)})+g_if_t(x_i)+\frac{1}{2}h_if_i^2(x_i)]+\Omega(f_t)+C \\ &= \sum_{i=1}^n[g_if_t(x_i)+\frac{1}{2}h_if_i^2(x_i)]+\Omega(f_t)+C \\ &=\sum_{i=1}^{n}\left[g_{i} w_{q\left(x_{i}\right)}+\frac{1}{2} h_{i} w_{q\left(x_{i}\right)}^{2}\right]+\gamma \cdot T+\lambda \cdot \frac{1}{2} \sum_{j=1}^{T} w_{j}^{2}+C \\ &=\sum_{j=1}^{T}\left[\left(\sum_{i \in I_{j}} g_{i}\right) w_{j}+\frac{1}{2}\left(\sum_{i \in I_{j}} h_{i}\right) w_{j}^{2}\right]+\gamma \cdot T+\lambda \cdot \frac{1}{2} \sum_{j=1}^{T} w_{j}^{2}+C \\ &= \sum_{j=1}^{T}\left[\left(\sum_{i \in I_{j}} g_{i}\right) w_{j}+\frac{1}{2}\left(\sum_{i \in I_{j}} h_{i}+\lambda\right) w_{j}^{2}\right]+\gamma \cdot T+C \end{aligned}$
对目标函数继续简化

$J\left(f_{t}\right)=\sum_{j=1}^{T}\left[\left(\sum_{i \in I_{j}} g_{i}\right) w_{j}+\frac{1}{2}\left(\sum_{i \in I_{j}} h_{i}+\lambda\right) w_{j}^{2}\right]+\gamma \cdot T+C$

定义：
$G_{j}=\sum_{i \in I_{j}} g_{i}, H_{j}=\sum_{i \in I_{j}} h_{i}$
从而目标函数表为：
$J\left(f_{t}\right)=\sum_{j=1}^{T}[G_{j} w_{j}+\frac{1}{2}\left(H_{j}+\lambda\right) w_{j}^{2} ]+\gamma \cdot T+C$
对 w 求偏导数
$\frac{\partial J\left(f_{t}\right)}{\partial w_{j}}=G_{j}+\left(H_{j}+\lambda\right) w_{j}=0\\{\color{Red} \Rightarrow w_{j}=-\frac{G_{j}}{H_{j}+\lambda}}$
带回目标函数
$\color{Red}J\left(f_{t}\right)=-\frac{1}{2} \sum_{j=1}^{T} \frac{G_{j}^{2}}{H_{j}+\lambda}+\gamma \cdot T$

1.2.xgboost 和 gbdt 区别

参考：http://wepon.me/

2.分裂结点算法

枚举可行的分割点，选择增益最大的划分——（精确的贪心法（Exact Greedy Algorithm））

$\operatorname{Gain}(\phi)=\frac{1}{2}\left[\frac{G_{L}^{2}}{H_{L}+\lambda}+\frac{G_{R}^{2}}{H_{R}+\lambda}-\frac{\left(G_{L}+G_{R}\right)^{2}}{H_{L}+H_{R}+\lambda}\right]-\gamma$

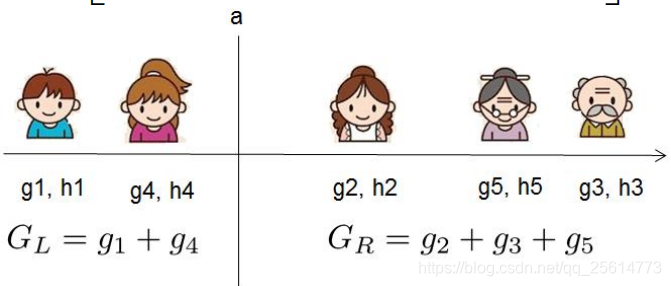
在这里插入图片描述

当数据量十分庞大，以致于不能全部放入内存时，Exact Greedy 算法就会很慢。因此XGBoost引入了近似的算法。即对每一个特征进行「值」采样。原来需要对每一个特征的每一个可能分割点进行尝试，采样之后只针对采样的点（分位数）进行分割尝试，这种方法很明显可以减少计算量，采样密度越小计算的越快，拟合程度也会越差，所以采样还可以防止过拟合
参考——XGB算法梳理

3.对缺失值处理

xgboost处理缺失值的方法和其他树模型不同。根据作者TianqiChen在论文[1]中章节3.4的介绍，xgboost把缺失值当做稀疏矩阵来对待，本身在节点分裂时不考虑缺失值的数值，但确定分裂的特征后，缺失值数据会被分到左子树和右子树呢？本文的处理策略是落在哪个孩子得分高，就放到哪里。如果训练中没有数据缺失，预测时出现了数据缺失，那么默认被分类到右子树。具体的介绍可以参考

4.优缺点

优点
1. xgBoosting支持线性分类器，相当于引入L1和L2正则化项的逻辑回归（分类问题）和线性回归（回归问题）；
2. xgBoosting对代价函数做了二阶Talor展开，引入了一阶导数和二阶导数；
3. 当样本存在缺失值是，xgBoosting能自动学习分裂方向；
4. xgBoosting借鉴RF的做法，支持列抽样，这样不仅能防止过拟合，还能降低计算；
5. xgBoosting的代价函数引入正则化项，控制了模型的复杂度，正则化项包含全部叶子节点的个数，每个叶子节点输出的score的L2模的平方和。从贝叶斯方差角度考虑，正则项降低了模型的方差，防止模型过拟合；
6. xgBoosting在每次迭代之后，为叶子结点分配学习速率，降低每棵树的权重，减少每棵树的影响，为后面提供更好的学习空间；
7. xgBoosting工具支持并行,但并不是tree粒度上的，而是特征粒度，决策树最耗时的步骤是对特征的值排序，xgBoosting在迭代之前，先进行预排序，存为block结构，每次迭代，重复使用该结构，降低了模型的计算；block结构也为模型提供了并行可能，在进行结点的分裂时，计算每个特征的增益，选增益最大的特征进行下一步分裂，那么各个特征的增益可以开多线程进行；
8. 可并行的近似直方图算法，树结点在进行分裂时，需要计算每个节点的增益，若数据量较大，对所有节点的特征进行排序，遍历的得到最优分割点，这种贪心法异常耗时，这时引进近似直方图算法，用于生成高效的分割点，即用分裂后的某种值减去分裂前的某种值，获得增益，为了限制树的增长，引入阈值，当增益大于阈值时，进行分裂；
缺点
1. xgBoosting采用预排序，在迭代之前，对结点的特征做预排序，遍历选择最优分割点，数据量大时，贪心法耗时，LightGBM方法采用histogram算法，占用的内存低，数据分割的复杂度更低；
2. xgBoosting采用level-wise生成决策树，同时分裂同一层的叶子，从而进行多线程优化，不容易过拟合，但很多叶子节点的分裂增益较低，没必要进行跟进一步的分裂，这就带来了不必要的开销；LightGBM采用深度优化，leaf-wise生长策略，每次从当前叶子中选择增益最大的结点进行分裂，循环迭代，但会生长出更深的决策树，产生过拟合，因此引入了一个阈值进行限制，防止过拟合.

5.sklearn参数

XGBoost的作者把所有的参数分成了三类：
1. 通用参数：宏观函数控制
2. Booster参数：控制每一步的booster(tree/regression)
3. 学习目标参数：控制训练目标

5.1.通用参数

参数	默认	说明
booster	gbtree	gbtree：基于树的模型 gbliner：线性模型
silent	0	1：静态模式开启，不会输出任何信息保持默认的0：帮助更好的理解模型
nthread	最大可能的线程	用来进行多线程控制算法自动检测cpu的全部核

5.2.booster参数

尽管有两种booster可以选择，只介绍tree booster （表现远胜过linear booster，一般linear booster很少使用）

参数	默认	说明
eta	0.3	- 和GBM中的 learning rate 参数类似 - 通过减少每一步的权重，可以提高模型的鲁棒性 - 典型值为0.01-0.2
min_child_weight	1	- 决定最小叶子节点样本权重和 - 和GBM的 min_child_leaf 参数类似，但XGBoost的是最小样本权重的和，而GBM是最小样本总数, - 用于避免过拟合。当它的值较大时，可以避免模型学习到局部的特殊样本 - 但是如果这个值过高，会导致欠拟合。需要使用CV来调整
max_depth	6	- 和GBM中的参数相同，这个值为树的最大深度 - 也是用来避免过拟合,max_depth越大，模型会学到更具体更局部的样本 - 需要使用CV函数来进行调优 - 典型值3-10
max_leaf_nodes		- 树上最大的节点或叶子的数量 - 可以替代max_depth的作用,如果生成的是二叉树,一个深度为n的树最多生成n $n^2$ 个叶子 - 定义了这个参数，GBM会忽略max_depth参数
gamma	0	- 在节点分裂时，只有分裂后损失函数的值下降了，才会分裂这个节点。Gamma指定了节点分裂所需的最小损失函数下降值 - 这个参数的值越大，算法越保守。这个参数的值和损失函数息息相关，所以是需要调整的
max_delta_step	0	- 这参数限制每棵树权重改变的最大步长。如果这个参数的值为0，那就意味着没有约束。如果它被赋予了某个正值，那么它会让这个算法更加保守 - 通常，这个参数不需要设置。但是当各类别的样本十分不平衡时，它对逻辑回归是很有帮助的 - 这个参数一般用不到
subsample	1	- 和GBM中的subsample参数一模一样。这个参数控制对于每棵树，随机采样的比例 - 减小这个参数的值，算法会更加保守，避免过拟合。但是，如果这个值设置得过小，它可能会导致欠拟合 - 典型值：0.5-1
colsample_bytree	1	- 和GBM里面的max_features参数类似。用来控制每棵随机采样的列数的占比(每一列是一个特征) - 典型值：0.5-1
colsample_bylevel	1	- 用来控制树的每一级的每一次分裂，对列数的采样的占比
lambda	1	- 权重的L2正则化项。(和Ridge regression类似)
alpha	1	- 权重的L1正则化项。(和Lasso regression类似) - 可以应用在很高维度的情况下，使得算法的速度更快
scale_pos_weight	1	- 在各类别样本十分不平衡时，把这个参数设定为一个正值，使算法更快收敛

5.3 学习目前参数

这个参数用来控制理想的优化目标和每一个结果的度量方法

参数	默认	说明
objective	reg:linear	- binary:logistic 二分类的逻辑回归 - multi:softmax 使用softmax的多分类(这种情况下，需要设置：num_class) -multi:softprob 返回每种数据属于各个类别的概率
eval_metric	取决于objective参数	- 回归默认rmse ,分类默认error
seed	0	- 随机数种子