基础篇2: 梯度、散度与旋度
本篇将介绍基于矢量运算所得到的三个重要物理概念:梯度(Gradient)、散度(Divergence)和旋度(Curl)。关于矢量的基本运算见前文:
燕飞残月天:基础篇1: CFD中的矢量195 赞同 · 11 评论文章
1. 哈密尔顿算子:∇ -nabla
在介绍梯度等概念之前,首先引入CFD非常常见的运算符之一:∇,它是某一物理量在三个坐标方向的偏导数的矢量和,定义如下:
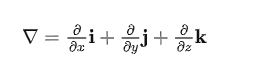
2. 梯度(Gradient)
当 ∇ 作用于标量 s 时即可得到该标量在空间中的梯度,下面列出了CFD中梯度的各种表达形式:

可以看出标量场的梯度是一个矢量场,它表示s 在空间某一位置沿某一方向的变化量。如果想要的到 s 在某一特定方向 el(方向 l 上的单位矢量) 上的梯度,即方向导数,则可以根据矢量点乘的几何意义来进行计算:
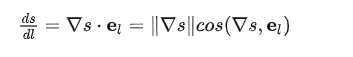
由此可见,当 cos(∇s,el)=1 ,即空间任意方向 l 与梯度方向一致时沿该方向具有最大梯度,因此 ∇s 代表了空间中任意点上梯度变化最大的方向和变化量,而且 ∇s 垂直于该点处的等值线或等值面。
3. 散度(Divergence)
根据矢量点乘的运算规则,∇ 与一个矢量的点乘是一个标量,它代表了矢量场的散度:

可以看出矢量的散度是一个标量,在CFD中它表示空间中某一区域流入或流出的矢量的多少,比较典型的例子有点源或者点汇。如下图是一个点汇,周围的矢量均流向该点。
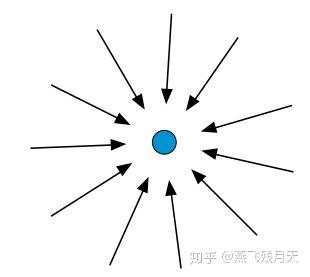
点汇周围的矢量场(旋度为0)
标量的梯度为矢量,因此对该矢量可以继续求散度,从而引入拉普拉斯算子∇2 :

上式代表了梯度的散度,可以看出标量经过拉普拉斯算子运算以后仍然是标量。
矢量的散度为标量,因此对该标量可以继续求梯度:

由这两个公式可以看出,拉普拉斯算子对标量的运算结果为标量、对矢量的运算结果为矢量。
4. 旋度(curl)
旋度是由 ∇ 与矢量的叉乘得到,它的运算结果是一个矢量,代表了矢量做旋转运动的方向和强度:

一个典型的有旋流场是点涡,如下图所示,它展示了一个散度为0的有旋矢量场。
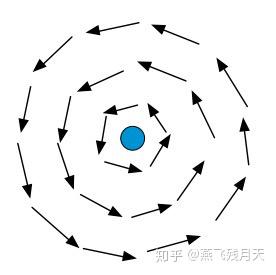
点涡周围的矢量场
以上介绍了基于矢量的梯度、散度和旋度计算方法和物理意义,下一篇将开始介绍张量在CFD中的应用。
参考资料
[1] Moukalled, F., Mangani, L., and Darwish, M.The Finite Volume Method in Computational Fluid Dynamics : An Advanced Introduction with OpenFOAM and Matlab. 2016.
数学基础 | 正交曲线坐标系中梯度、散度、旋度的理解与记忆
对学过高数的人来说,对计算梯、散、旋的三个公式应该是记得滚瓜烂熟了——

然而这些只是直角坐标系中的特殊情况,在常见的球坐标系、柱坐标系中,或者说在一般的曲线正交坐标系中,这些公式并不适用。
在电动力学、数理方法中会首先接触到正交曲线坐标系,其中的梯度、散度、旋度以及拉普拉斯算符形式如下,

在学习过程中,这么长的公式确实没必要花功夫去死记硬背,但记住这些式子会很有用——因为物理里面经常用到,每次翻书太麻烦了。实际上,这些看起来非常复杂的式子,只要记住其几何意义,就会很自然地记住,并不需要死记硬背。
这篇文章就是帮助初学者快速理解和记忆这些式子。
1 拉梅系数
在上面的一堆式子中出现的 hi 称为拉梅系数。可以通过如下方法计算与定义:

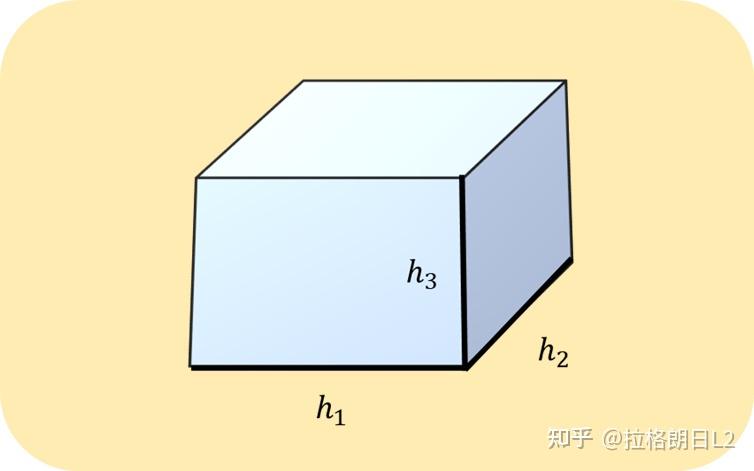
Figure1-1 体积元
直角坐标系最简单,它的拉梅系数都是1,所以梯散旋的计算如本文最开始的三个公式那样简单,而同样常见的球坐标系和柱坐标系就没那么简单了。
这里可以回忆一下多元微积分中遇到的雅克比行列式,那里推导了球坐标系和柱坐标系的体元和线元。
2 梯度
我们来回顾一下梯度的定义:
梯度表示某一函数在该点处的方向导数沿着该方向取得最大值,即函数在该点处沿着该方向变化最快。
以 u1 方向为例,这个方向的导数为(结合图2-1),

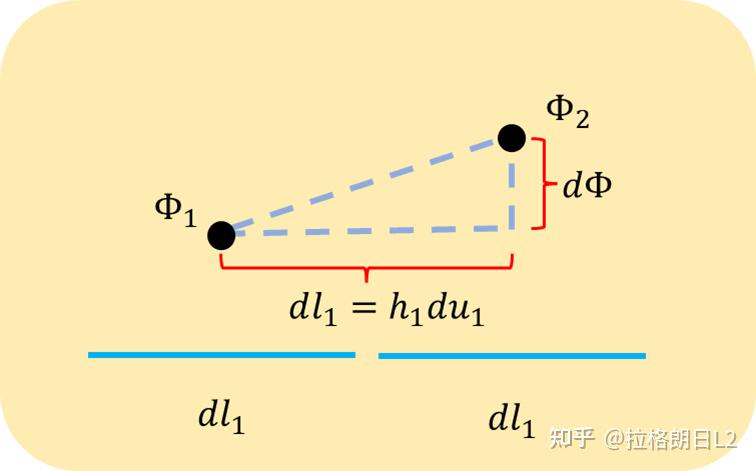
Figure2-1 方向导数
其他方向同理,可以得到,

3 散度
散度的几何意义是:单位体积内的通量——通量密度。

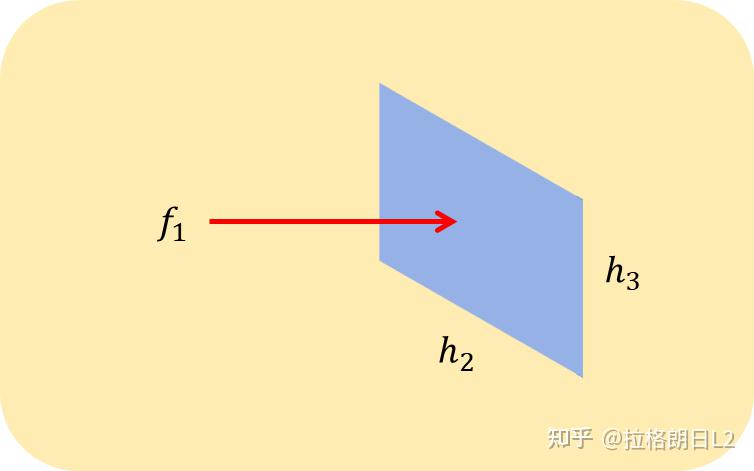
Figure3-1 通量密度

4 旋度
旋度的几何意义是:单位面积内的环量——环量密度。
既然是环量,那必然要乘上线元长度(图4-1),和熟知的直角坐标形式类比一下,就是这样的,

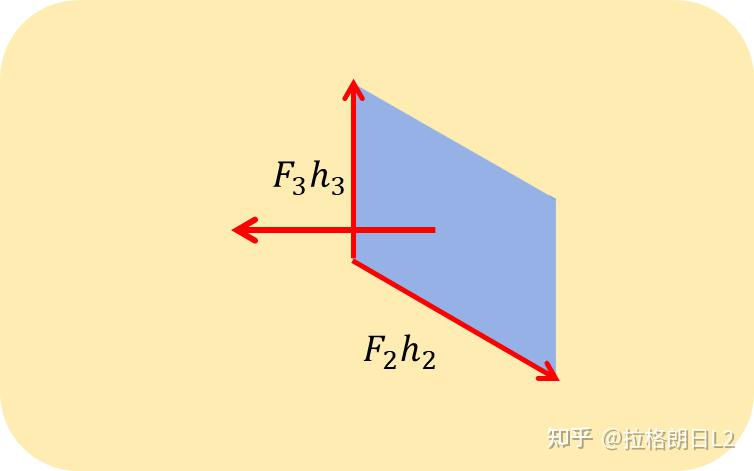
Figure4-1 环量密度

5 拉普拉斯算符
标量场梯度的散度就是拉普拉斯,

这是新专栏的第一篇文章,之后打算写物理和天文的相关知识,帮助大家理解
https://zhuanlan.zhihu.com/p/452461912
至此,麦克斯韦方程组的四个方程:描述静电的高斯电场定律、描述静磁的高斯磁场定律、描述磁生电的法拉第定律和描述电生磁的安培-麦克斯韦定律的微分形式就都说完了。把它们都写下来就是这样:

高斯电场定律说电场的散度跟这点的电荷密度成正比。
高斯磁场定律说磁场的散度处处为0。
法拉第定律说感生电场的旋度等于磁感应强度的变化率。
安培-麦克斯韦定律说感生磁场的旋度等于电流密度和电场强度变化率之和。
这里最引入注目的就是▽算子了,它以点乘和叉乘的方式组成的散度▽·和旋度▽×构成了麦克斯韦方程组微分形式的核心,这也是为什么我要花那么大篇幅从偏导数、矢量点乘一步步给大家引出▽算子的原因。也因为如此,微分篇的数学部分比积分篇要多得多得多,相对也要难以理解一些,所以大家要稍微有耐性一点。

从思想上来讲,微分形式和积分形式表达的思想是一样的,毕竟它们都是麦克斯韦方程组。它们的差别仅仅在于积分形式是从宏观的角度描述问题,我们面对的宏观上的曲面,所以要用通量和环流来描述电场、磁场;而微分形式是从微观的角度来描述问题,这时候曲面缩小都无穷小,我们面对的东西就变成了一个点,所以我们使用散度和旋度来描述电场、磁场。这一点是特别要强调的:通量和环流是定义在曲面上的,而散度和旋度是定义在一个点上的。我们可以说通过通过一个曲面的通量或者沿曲面边界的环流,但是当我们在说散度和旋度的时候,我们都是在说一个点的散度和旋度。理解了这些,你再回过头去看看麦克斯韦方程组的积分形式:

我们只不过把定义在曲面上的通量和环流缩小到了一个点,然后顺势在这个点上用利用通量和环流定义了散度和旋度。因为定义散度和旋度分别还除了一个体积和面积,所以我们积分方程的右边也都相应的除了一个体积和面积,然后就出现了电荷密度ρ(电荷Q除以体积V)和电流密度J(电流I除以面积S),电通量和磁通量那边除以一个体积和面积就剩下电场强度E和磁感应强度B的变化率,仅此而已。如果我们从这种角度去看麦克斯韦方程组的积分形式和微分形式,你就会觉得非常的自然和谐。给出积分形式,你一想散度和旋度的定义,就可以立马写出对应的微分形式;给出微分形式,再想一想散度和旋度的定义,也能立刻写出对应的积分形式。当我想从宏观入手的时候,我看到了曲面上的通量和环流;当我想从微观入手的时候,我也能立马看到一个点上的散度和旋度。积分和微分形式在这里达成了一种和谐的统一。

























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








