Dijkstra求最短路与次短路

花了一个晚上加上午两节课的时间来思考这个问题，一开始进了个误区，后来发现不对，找到了正确思路，现在来做个总结

最短路：

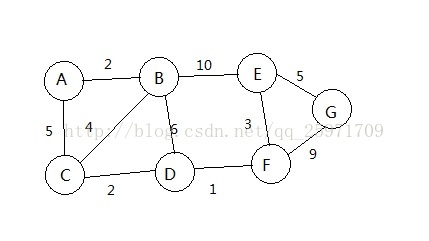
假设有如下 无向图：

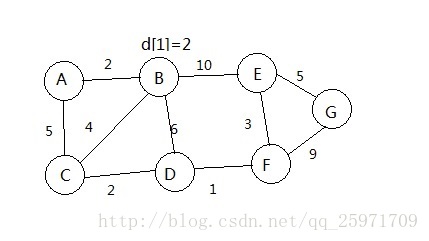
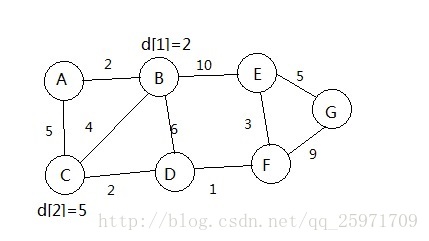
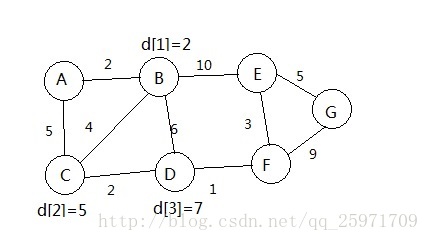
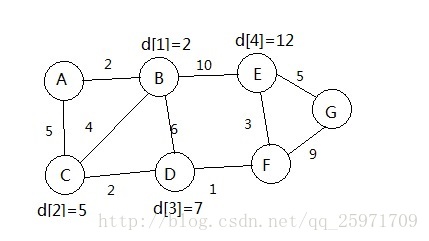
每条边有权，要求从A到G的最短路，设数组d[i]用来记录每个点到A的最短路，D[][]用来记录权值d[0]=0。先来说一下我一开始的误区，在看了一些介绍这个算法的文章后我大概知道了是要一步一步来更新每个点的最小值。于是我是这样想的从A到B遍历，A到A的距离是0，然后是B，d[1]=D[0][1]=2，然后是C，d[2]=min(D[0][2], d[1]+D[1][2])=5，接下来是D，d[3]=min(d[1]+D[1][3], d[2]+D[2][3])，我用图来解释这个过程：

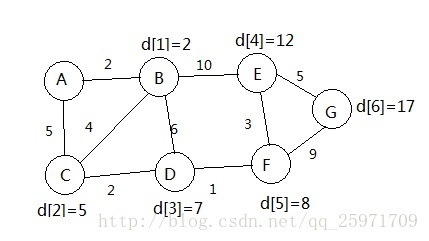
最后结果是的d[6]=17，但实际上问题在E和F上已经出现了，由于我们先算的是E，在这时数组里F的距离还是无穷大，所以E只能从B得到一个2，再加上BE=10就是12。但算过F后发现，E的最短距离应该是F的8加上EF=3，结果是11，于是G的最短距离应该是11+5=16。问题就在于我们按ABCDEFG的顺序依次简单地求当前点的最短距离时，每个点的距离只能更新一次，无法从后续计算中得到该点更近的距离。这种方法中”当前点“是未求值的点，而正确的做法应该把”当前点“定为已求过的点。也就是说，我们要做的是从该点出发求临近点的最小值，而不是站在该点，用已求过值的临近点来求该点的值。

正确的过程应该是这样，计算每个点时都要用这个转移方程 d[i]=min(d[i], d[j]+D[i][j])，其中j是当前点，i是与j相连的点：

从A开始，A与B，C相连，更新B，C，d[1]=2, d[2]=5；

转到B，B与CDE相连，d[2]=min(d[2], d[1]+D[2][1])=5，同理，d[3]=7, d[4]=12

…………

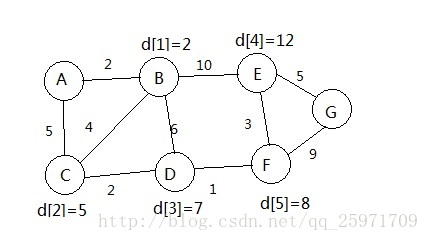
到F时，F与DEG相连，所以在更新E的时候就会有d[4]=min(d[4], d[5]+D[5][4])=11;

这样做就可以用在E之后的F来更新E的值。

这一过程可以直接将d[i]放到循环里实现，也可以用优先队列，将(d[i], i)入列。当从某个点j求得的d[i]大于数组中已有的d[i]时，就不入列。这个优先队列的过程在纸上画一画就很清楚了。

忘了说了，在转移到下一个点时必须转移到d[i]最小的点，这个条件非常重要！

次短路：

接下来是次短路。次短路的做法和最短路几乎一模一样。在过程中同时记录每个点的最短路和次短路，然后用同样的方法更新每个点的值。要注意的就是计算与当前点相邻点的次短路时需要同时用到该点的最短路和次短路，也就是要求三个值的最小值：min（d2[i], d[j]+D[i][j], d2[j]+D[i][j]），其中数组d2[i]就是每点的次短路。要注意的是要先求最短路再求次短路，保证最短路小于次短路。