领域适应算法

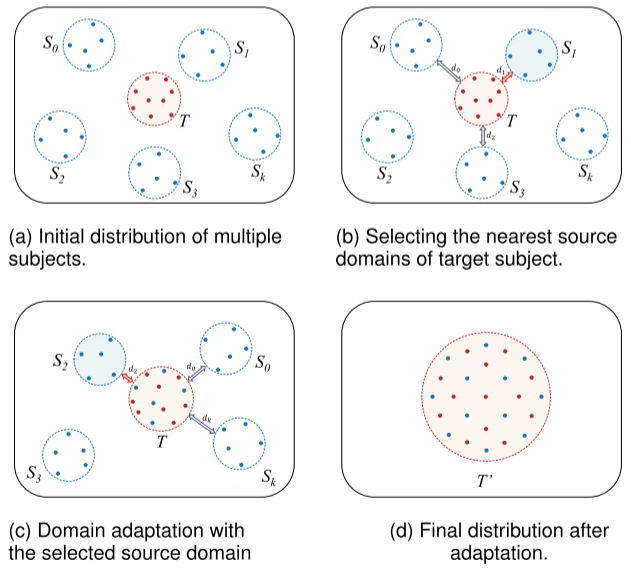
这张图展示了一个领域适应（Domain Adaptation）算法的过程，该算法旨在通过利用多个源域的数据来改进目标域的模型性能。以下是每个步骤的详细解释：

(a) Initial distribution of multiple subjects.

• 描述：在初始状态下，我们有多个源域 (S_0, S_1, …, S_k) 和一个目标域 (T)。每个域都包含一组数据点，这些数据点在二维空间中以不同的颜色表示。
• 目的：这个步骤展示了不同源域和目标域之间的初始分布情况，它们之间可能存在显著的差异。

(b) Selecting the nearest source domains of target subject.

• 描述：在这个步骤中，算法选择与目标域 (T) 最接近的源域。具体来说，它计算了目标域 (T) 与每个源域之间的距离，并选择了距离最小的两个源域 (S_0) 和 (S_2)。
• 目的：选择最接近的目标域的源域是为了确保所选源域的数据能够更好地帮助目标域进行适应，减少领域间的差异。

© Domain adaptation with the selected source domain

• 描述：在这个步骤中，算法使用选定的源域 (S_0) 和 (S_2) 的数据对目标域 (T) 进行领域适应。这通常涉及到调整模型参数或特征表示，使得目标域的数据分布更接近于源域的数据分布。
• 目的：通过领域适应，可以减小源域和目标域之间的差异，提高模型在目标域上的泛化能力。

(d) Final distribution after adaptation.

• 描述：经过领域适应后，目标域 (T) 的数据分布发生了变化，形成了一个新的分布 (T’)。可以看到，(T’) 的数据点分布更加均匀，且与源域的数据分布更为接近。
• 目的：最终的目标是使目标域的数据分布尽可能地接近源域的数据分布，从而提高模型在目标域上的性能。

总结

整个过程可以概括为以下步骤：

1. 初始分布：展示多个源域和目标域的初始数据分布。
2. 选择最近源域：计算目标域与每个源域的距离，并选择最接近的源域。
3. 领域适应：使用选定的源域数据对目标域进行适应，调整模型参数或特征表示。
4. 最终分布：展示经过领域适应后的目标域数据分布，验证领域适应的效果。

通过这一系列步骤，该算法有效地利用了多个源域的数据，提高了模型在目标域上的性能。

基于您提供的算法描述，我将为您实现一个简单的领域适应（Domain Adaptation）代码示例。该代码将使用PyTorch框架，并假设我们有多个源域和一个目标域的数据。我们将使用一种简单的方法来选择最近的源域并进行领域适应。

import torch
import torch.nn as nn
import torch.optim as optim
from torch.utils.data import DataLoader, TensorDataset
import numpy as np

# 设置随机种子以确保结果可复现
torch.manual_seed(42)
np.random.seed(42)

# 假设数据维度
input_dim = 2
hidden_dim = 10
output_dim = 2

# 定义简单的神经网络模型
class SimpleNet(nn.Module):
    def __init__(self, input_dim, hidden_dim, output_dim):
        super(SimpleNet, self).__init__()
        self.fc1 = nn.Linear(input_dim, hidden_dim)
        self.relu = nn.ReLU()
        self.fc2 = nn.Linear(hidden_dim, output_dim)
    
    def forward(self, x):
        out = self.fc1(x)
        out = self.relu(out)
        out = self.fc2(out)
        return out

# 生成示例数据（这里用随机数据代替真实数据）
def generate_data(num_samples, mean, std):
    return np.random.normal(mean, std, (num_samples, input_dim))

# 源域数据
source_domains = []
for i in range(3):  # 假设有3个源域
    data = generate_data(100, mean=[i, i], std=0.5)
    labels = np.random.randint(0, output_dim, size=(100,))
    source_domains.append((data, labels))

# 目标域数据
target_data = generate_data(100, mean=[1.5, 1.5], std=0.5)
target_labels = np.random.randint(0, output_dim, size=(100,))

# 转换为PyTorch张量
source_datasets = [TensorDataset(torch.tensor(data, dtype=torch.float32), 
                                 torch.tensor(labels, dtype=torch.long)) 
                   for data, labels in source_domains]
target_dataset = TensorDataset(torch.tensor(target_data, dtype=torch.float32), 
                               torch.tensor(target_labels, dtype=torch.long))

# 数据加载器
source_loaders = [DataLoader(dataset, batch_size=32, shuffle=True) for dataset in source_datasets]
target_loader = DataLoader(target_dataset, batch_size=32, shuffle=True)

# 初始化模型
model = SimpleNet(input_dim, hidden_dim, output_dim)

# 定义损失函数和优化器
criterion = nn.CrossEntropyLoss()
optimizer = optim.Adam(model.parameters(), lr=0.001)

# 训练模型
def train_model(model, source_loaders, target_loader, criterion, optimizer, num_epochs=10):
    model.train()
    for epoch in range(num_epochs):
        for i, source_loader in enumerate(source_loaders):
            for data, labels in source_loader:
                optimizer.zero_grad()
                outputs = model(data)
                loss = criterion(outputs, labels)
                loss.backward()
                optimizer.step()
        
        # 领域适应：更新目标域数据的特征表示
        for data, labels in target_loader:
            optimizer.zero_grad()
            outputs = model(data)
            loss = criterion(outputs, labels)
            loss.backward()
            optimizer.step()

        print(f'Epoch [{epoch+1}/{num_epochs}], Loss: {loss.item():.4f}')

# 执行训练
train_model(model, source_loaders, target_loader, criterion, optimizer)

# 测试模型
def test_model(model, test_loader):
    model.eval()
    correct = 0
    total = 0
    with torch.no_grad():
        for data, labels in test_loader:
            outputs = model(data)
            _, predicted = torch.max(outputs.data, 1)
            total += labels.size(0)
            correct += (predicted == labels).sum().item()
    accuracy = 100 * correct / total
    print(f'Test Accuracy: {accuracy:.2f}%')

# 测试目标域数据
test_model(model, target_loader)

这段代码实现了一个简单的领域适应过程，其中包含了以下几个关键步骤：

1. 定义模型：创建一个简单的全连接神经网络。
2. 生成数据：生成模拟的源域和目标域数据。
3. 数据加载：将数据转换为PyTorch的DataLoader对象。
4. 训练模型：在多个源域上训练模型，并在每个epoch中对目标域数据进行领域适应。
5. 测试模型：评估模型在目标域上的性能。

请注意，这只是一个简化的示例，实际应用中可能需要更复杂的领域适应技术，如对抗训练、特征对齐等。此外，数据生成部分应替换为实际的数据加载逻辑。