WebRtc中视频JitterBuffer的Jitterdelay估计方法

研究起因

之前在做项目的时候，有过专门的移植过WebRtc中的视频JitterBuffer，当时就很好奇内部是如何实现jitter的抖动的估计的，一直想好好研究一下，最近也是下定决心想要把这一点吃透，平时闲暇花时间仔细的研究了一下，在此做一下记录，以便后面有兴趣的同学一同研究。

解决的问题

WebRtc中的JitterBuffer位于拉流链路部分，是处理视频帧的关键模块。主要提供了以下两项功能：
1、通过RTP包解析组出完整的视频帧
2、通过记录组帧相关流程上的时间信息，预测网络抖动，进而控制视频帧的输出时间保证
第一个功能是RTP协议相关的，第二个功能与网络相关，也是JitterBuffer控制视频播放质量的核心，下面主要针对第二项进行讨论。

抖动从哪里来

了解网络的同学可能都见过下面的这幅图：

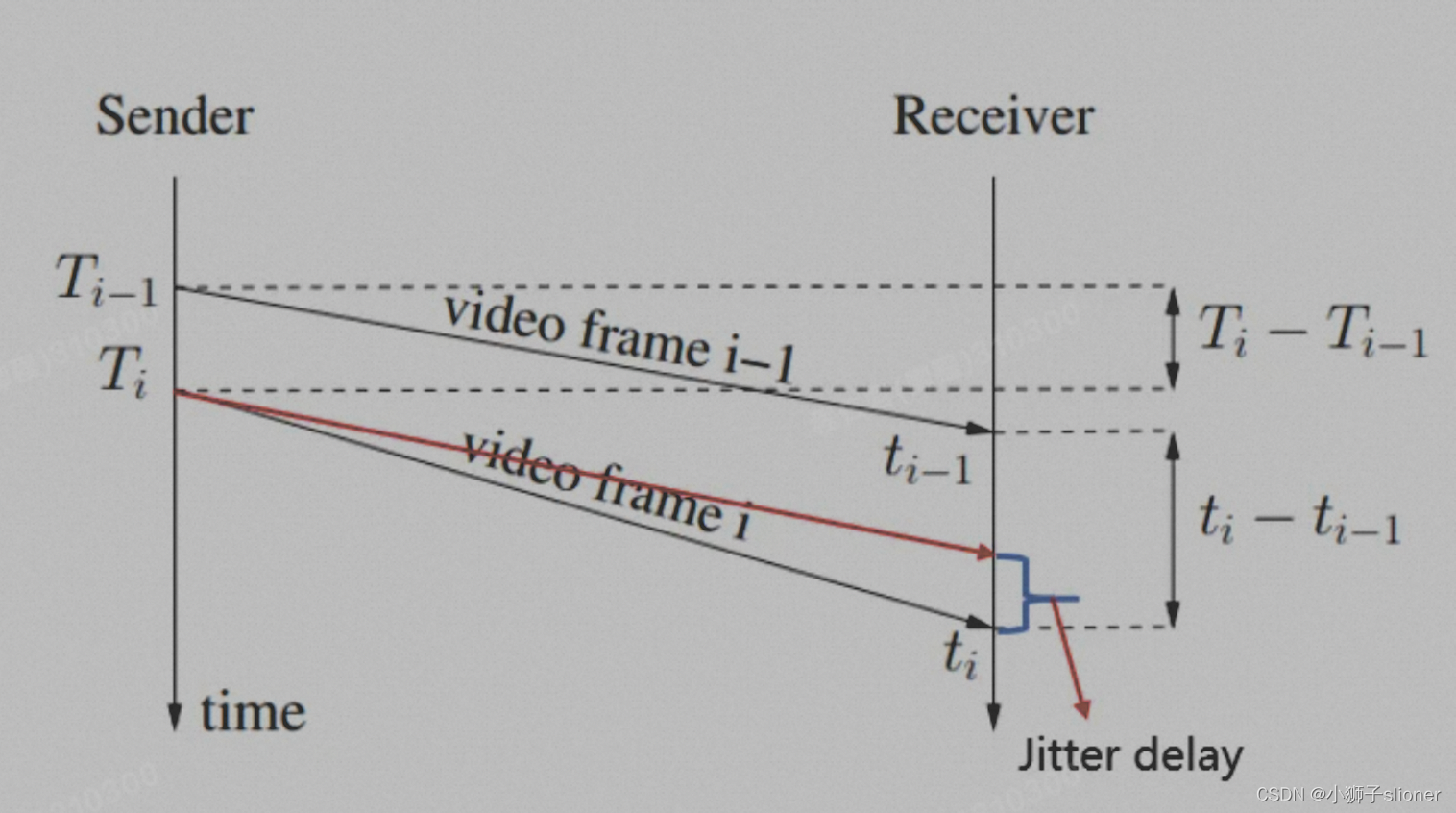
两个视频帧在拆成RTP包之后放到网络中传播，由于丢包，乱序等一系列的网络不确定性，那么组帧的时间和实际发送包的时间是有一个时间差的，这个时间差即为JitterDelay。

如何获取抖动

需要明确的一点是，这个时间差我们可以根据时间戳以及拉流端时机获取到完整帧的时间来计算得到，那么这时我们就会思考，是否有一种方法能让我们获取到这个JitterDelay时间的具体数值，那么当我的每个帧输出保证有一个固定的delay时间，那么就可以保证流畅的视频播放了。这种通过多次采样来获取到估计值的方法可以用求平均的方式得到，为了更加稳定的获取到这个估计值，我们可以采用更进阶的卡尔曼滤波来进行数据处理，即可获取到更优的估计结果。
那么也就引入了今日的主题，如何通过卡尔曼滤波更好的处理并获取估计的JitterDelay？

卡尔曼滤波

具体关于卡尔曼滤波的细节我这里就不展开了，有很多链接讲的很好，我这里推荐：

B站DR_CAN的卡尔曼滤波器的课程，他的B站主页为：https://space.bilibili.com/230105574

有兴趣的可以反复研读，这里主要给出了几个公式后面会用到：

theta^(i) = theta

公式推导

建模
首先我们要明确我们的输入变量是什么，即输入变量为每次采样与前一次的差值，用d(i)来表示，那么我们可以用以下式子进行建模：

d(i) = t(i) - t(i - 1) - (T(i) - T(i - 1))
     = L(i) / C(i) - L(i - 1) / C(i - 1) + w(i)
     = dL(i) / C(i) + w(i)
     = dL(i) / C(i) + m(i) + v(i)   ---------- 式1
d(i) : JitterDelay,我们可以观测出
L(i) : 第i帧的大小，可以观测得到
C(i) : 第i帧传输时的信道传输速率
w(i): 第i帧传输时的随机噪声，可以认为组成为 
W(i) =  m(i) + v(i)
m(i) :第i次传输时的网络排队延时
v(i) : 代表过程中的观测噪声（如最大帧数据量和平均每帧数据量的计算误差，时间同步等）符合正态分布，期望为0，协方差矩阵为R

在这个式子中，我们想要实际求出的估计值有两个，一个是C(i)，一个是w(i)，那么这两个估计值组成了卡尔曼滤波中的两个误差变量，后续我们需要针对这两个变量进行卡尔曼滤波的矩阵计算，以上即对d(i)进行建模的过程，找到了jitterdelay的相关因子C(i)和w(i)。
依据卡尔曼滤波进行计算
下面我们用卡尔曼滤波进行估计C(i)和w(i)

另我们的观测变量C(i)和w(i)组成了观测结果矩阵：

theta(i) = [1/C(i) m(i)]^T

那么 式1 可改写为矩阵运算

d(i) = H * theta(i) + v(i)
H = [dL(i) 1]
h_bar = H^T

根据卡尔曼滤波的状态转移方程可以获取如下公式：

theta^(i) = theta^-(i) + K(d(i) - H * theta^-(i ))
      = theta^(i - 1) + K(d(i) - H * theta^(i -1))

theta^-：为先验估计（即还未采用卡尔曼滤波处理时的估计值），用上次迭代的后验估计值来替代（已知）
H:为状态转移参数，由d(i)构成（已知）
在这里面未知的参数为K(卡尔曼系数)，其余的都可以在迭代中获取到，那么k的计算公式如下（卡尔曼系数）：

K = (P^-(i) * H^T) / (H * P^-(i)*H^T + R)
  = ((E(i - 1) + Q(i)) * h_bar(i)) / (var_h_hat(i) + h_bar(i)^T * (E(i - 1) + Q(i)) * h_bar(i)) 

P^-(i)：为当前帧的先验误差协方差，由E(i - 1) 计算而来
E(i) : 为后验误差协方差，使用的为i-1的结果（已知）
Q(i) : 为过程噪声，符合正态分布，期望为0，协方差矩阵为Q,代码中为固定值（已知）
var_h_hat(i)：为测量误差协方差，使用指数平均滤波器，计算方法在在Gcc中给出，与帧率有关（已知）

var_v_hat(i) = max(beta * var_v_hat(i - 1)) + (1 - beta) * z(i)^2, 1)
beta = (1 - chi)^(30 / (1000 * f_max))

z(i)为网络残差(当前测量值 - 上一次估计值）（已知）

z(i) = theta(i) - theta^(i - 1)

此时还差E(i)的计算方法没有给出，后验估计误差协方差

e(i) = theta(i) - theta^(i)
E(i) = E(e(i) * e(i)^T)
     = E((theta(i) - theta^()) * (theta(i) - theta^())^T)
     = (I - k_bar(i) * H) * P^-(i))
     = (I - k_bar(i) * H) * (E(i - 1) + Q(i)

那么这个时候，所有的估计参数均为已知，可以不断进行迭代,迭代步骤为：
1、计算先验估计的误差协方差
2、矫正卡尔曼系数
3、计算后验估计值
4、计算后验估计的误差协方差

代码流程分析

代码主要位于VCMJitterEstimator模块中

// Updates Kalman estimate of the channel
// The caller is expected to sanity check the inputs.
void VCMJitterEstimator::KalmanEstimateChannel(int64_t frameDelayMS,
                                               int32_t deltaFSBytes) {
  double Mh[2];
  double hMh_sigma;
  double kalmanGain[2];
  double measureRes;
  double t00, t01;

  // Kalman filtering

  // Prediction
  // M = M + Q
  // 首先计算E(i - 1) + Q(i)，先验误差协方差
  _thetaCov[0][0] += _Qcov[0][0];
  _thetaCov[0][1] += _Qcov[0][1];
  _thetaCov[1][0] += _Qcov[1][0];
  _thetaCov[1][1] += _Qcov[1][1];

  // Kalman gain
  // K = M*h'/(sigma2n + h*M*h') = M*h'/(1 + h*M*h')
  // h = [dFS 1]
  // Mh = M*h'
  // hMh_sigma = h*M*h' + R
  // 计算出卡尔曼滤波系数的分子 ((E(i - 1) + Q(i)) * h_bar(i))
  Mh[0] = _thetaCov[0][0] * deltaFSBytes + _thetaCov[0][1];
  Mh[1] = _thetaCov[1][0] * deltaFSBytes + _thetaCov[1][1];
  // sigma weights measurements with a small deltaFS as noisy and
  // measurements with large deltaFS as good
  if (_maxFrameSize < 1.0) {
    return;
  }
  //计算var_h_hat(i)
  double sigma = (300.0 * exp(-fabs((double)(deltaFSBytes)) /
                              (1e0 * _maxFrameSize)) +
                  1) *
                 sqrt(_varNoise);
  if (sigma < 1.0) {
    sigma = 1.0;
  }
  // 卡尔曼的计算式分母(var_h_hat(i) + h_bar(i)^T * (E(i - 1) + Q(i)) * h_bar(i))
  hMh_sigma = deltaFSBytes * Mh[0] + Mh[1] + sigma;
  if ((hMh_sigma < 1e-9 && hMh_sigma >= 0) ||
      (hMh_sigma > -1e-9 && hMh_sigma <= 0)) {
    assert(false);
    return;
  }
  // 计算卡尔曼系数
  kalmanGain[0] = Mh[0] / hMh_sigma;
  kalmanGain[1] = Mh[1] / hMh_sigma;

  // Correction
  // theta = theta + K*(dT - h*theta)
  measureRes = frameDelayMS - (deltaFSBytes * _theta[0] + _theta[1]);
  // 根据卡尔曼的递推公式计算出估计值
  _theta[0] += kalmanGain[0] * measureRes; // 这个是信道传输速率
  _theta[1] += kalmanGain[1] * measureRes; // 这里是排队延时

  if (_theta[0] < _thetaLow) {
    _theta[0] = _thetaLow;
  }

  // M = (I - K*h)*M
  
  t00 = _thetaCov[0][0];
  t01 = _thetaCov[0][1];
  // 更新E(i) = (I - k_bar(i) * H) * (E(i - 1) + Q(i)
  _thetaCov[0][0] = (1 - kalmanGain[0] * deltaFSBytes) * t00 -
                    kalmanGain[0] * _thetaCov[1][0];
  _thetaCov[0][1] = (1 - kalmanGain[0] * deltaFSBytes) * t01 -
                    kalmanGain[0] * _thetaCov[1][1];
  _thetaCov[1][0] = _thetaCov[1][0] * (1 - kalmanGain[1]) -
                    kalmanGain[1] * deltaFSBytes * t00;
  _thetaCov[1][1] = _thetaCov[1][1] * (1 - kalmanGain[1]) -
                    kalmanGain[1] * deltaFSBytes * t01;

  // Covariance matrix, must be positive semi-definite
  assert(_thetaCov[0][0] + _thetaCov[1][1] >= 0 &&
         _thetaCov[0][0] * _thetaCov[1][1] -
                 _thetaCov[0][1] * _thetaCov[1][0] >=
             0 &&
         _thetaCov[0][0] >= 0);
}

利用以上代码不断更新即可获取估计到的网络速率和随机噪声，随后利用函数即可获取到对应的抖动时延

double VCMJitterEstimator::CalculateEstimate() {
  // NoiseThreshold的计算中用到_theta[1]
  double ret = _theta[0] * (_maxFrameSize - _avgFrameSize) + NoiseThreshold();

  // A very low estimate (or negative) is neglected
  if (ret < 1.0) {
    if (_prevEstimate <= 0.01) {
      ret = 1.0;
    } else {
      ret = _prevEstimate;
    }
  }
  if (ret > 10000.0) {  // Sanity
    ret = 10000.0;
  }
  _prevEstimate = ret;
  return ret;
}