【算法】质因式分解

1. 概述

数学定理：任何一个大于2的正整数都可以被分解为质数的乘积。

2. 质因式分解策略

质因式分解策略：

• 从2开始递增作为因子factor进行分解，到 sqrt(n) + 1 为止，因为如果一个数如果能够被因式分解，那么它的因子不会大于 sqrt(n) + 1；
• 当整数n能整出factor时，则factor就是它的一个质因子，连续除以该因子直到不能整除为止；
• 在这个过程中不用担心出现非质数的因子，因为质数的因子也可以被因式分解为质数的乘积，在之前的过程中已经被分解了，留下的都是只能被质数整除的部分。

3. 代码及测试

C++

#include <iostream>
#include <vector>
#include <unordered_map>

using namespace std;

class Factorization {
public:
    string factorize(int n) {
        unordered_map<int, int> out;
        int temp = (int) (sqrt(n) + 1);
        for (int i = 2; i <= temp; i++) {
            if (n % i == 0) {
                while (n % i == 0) {
                    out[i]++;
                    n /= i;
                }
            }
            if (n == 1) break;
        }
        if (n != 1) {
            out[n] = 1;
        }
        string res;
        for (auto& p: out) {
            int factor = p.first;
            int cnt = p.second;
            if (res.empty()) {
                res += std::to_string(factor);
                cnt--;
            }
            while (cnt-- > 0) {
                res += " * " + std::to_string(factor);
            }
        }
        return res;
    }
};


int main() {
    Factorization factorization;
    int n;
    while (true) {
        cin >> n;
        string res = factorization.factorize(n);
        cout << n << " = " << res << endl;
    }
    return 0;
}

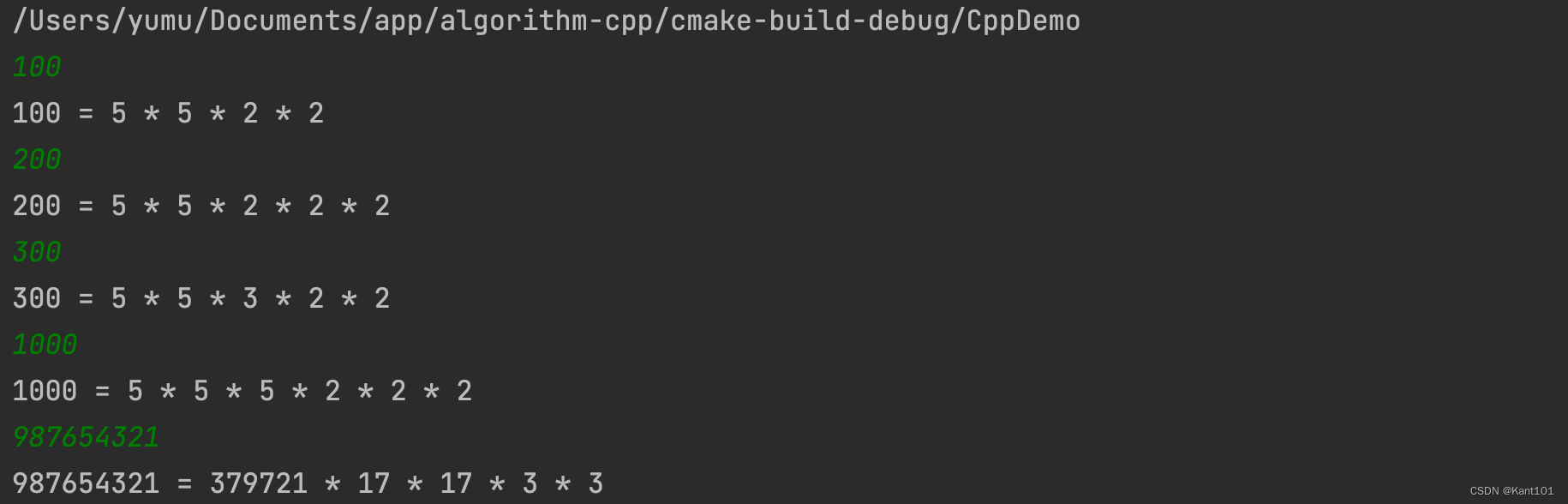
JAVA

package demo;

import java.util.LinkedHashMap;
import java.util.Scanner;

/**
 * 质因式分解，任何一个大于等于2的整数都可以被分解为几个质数的乘积
 *
 * @author yumu
 * @date 2022/8/16
 */
public class Factorization {

    /**
     * 对传入的正整数进行质因式分解
     *
     * @param n 待质因式分解的正整数
     * @return 得到的质因式分解表达式
     */
    public String factorize(int n) {
        LinkedHashMap<Integer, Integer> out = new LinkedHashMap<>();
        int temp = (int) Math.sqrt((double) n) + 1;
        for (int i = 2; i <= temp; i++) {
            if (n % i == 0) {
                out.put(i, 0);
                while (n % i == 0) {
                    out.put(i, out.get(i) + 1);
                    n /= i;
                }
            }
            if (n == 1) break;
        }
        if (n != 1) {
            out.put(n, 1);
        }
        StringBuilder res = new StringBuilder();
        for (int factor: out.keySet()) {
            int cnt = out.get(factor);
            if (res.length() == 0) {
                res.append(factor);
                cnt--;
            }
            while (cnt > 0) {
                res.append(" * ").append(factor);
                cnt--;
            }
        }
        return res.toString();
    }

    public static void main(String[] args) {
        Factorization factorization = new Factorization();
        Scanner input = new Scanner(System.in);
        int n;
        while (true) {
            n = input.nextInt();
            String res = factorization.factorize(n);
            System.out.println(n + " = " + res);
        }
    }
}

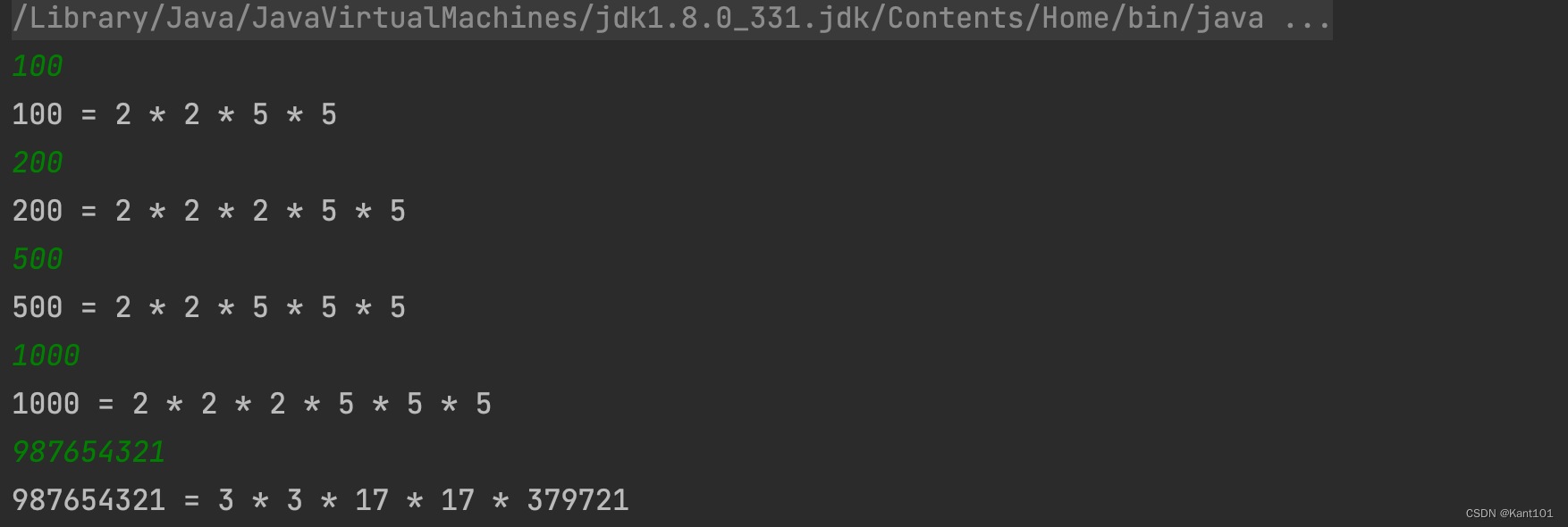
Python

import numpy as np


def factor(n, a, b):
    index = 0
    temp = int(np.sqrt(n) + 1)
    now = n
    for i in range(2, temp + 1):
        if now % i == 0:
            a.append(i)
            b.append(0)
            while now % i == 0:
                b[index] += 1
                now /= i
            index += 1
    if now != 1:
        a.append(int(now))
        b.append(1)


if __name__ == '__main__':
    while True:
        n = int(input())
        a = []
        b = []
        factor(n, a, b)
        print(n, '= ', end='')
        num = len(a)
        for i in range(0, num):
            for j in range(0, b[i]):
                if i == 0 and j == 0:
                    print(a[i], end='')
                else:
                    print(' *', a[i], end='')
        print()