进制概括与转化

目录

一.数制的基本内容

1数制的概念

2常用进制的分类和表达方式

3.进制的基本运算规则

二.数制之间的相互转换

1.十进制转二进制，八进制，十六进制。（连除法）

1.1十进制转二进制

1.2十进制转八进制

1.3十进制数转十六进制

2.二进制，八进制，十六进制转十进制。

2.1二进制转十进制

2.2八进制转十进制

2.3十六进制转十进制

3.二进制转八进制八进制，十六进制（分组连乘）

3.1二进制转八进制

3.2二进制转十六进制

4.八进制，十六进制转二进制（分组连除）

4.1八进制转二进制

4.2十六进制转二进制

---

一.数制的基本内容

1数制的概念

数制：也叫“计数制”，是使用固定的符号和统一的标准来表示数值的方法。

进制：也叫“进位计数制”，是人为规定的带进位的一种计数方法。比如日常使用的十进制数，就是逢十进一。进制包括三个要素，即数位，基数和位权。

数位：表示数字符号在数中所在的位置。比如十进制数4，这个符号4当前所处的特定位置。

基数：表示在某种进位计数制中数位上所能使用的数字符号的个数。比如十进制的基数是10。

位权：表示在某种进位计数制中，数位所代表的大小，即处在某一位上的数字所代表的数值大小。比如十进制数456，第一位的位权是100，第二位的位权是10，第三位的位权是1，以此类推。

2常用进制的分类和表达方式

在计算机的汇编语言中，常用的进制有二进制，八进制，十进制和十六进制。

数制的表示方式有两种：一种是数字表示法，一种是字母后缀表示法。

数字表示法：

如：（10010011）2 代表二进制数

       （7623）8 代表八进制数

字母后缀表示法：

二进制 B （binary）

八进制 O （octal）

十进制 D （decimal）

十六进制 H （hexadecimal）

如：（10010011）B 代表二进制数

       （7623）O 代表八进制数

3.进制的基本运算规则

二进制：逢二进一

二进制基数为2，数值只使用1或者0来表示。

八进制：逢八进一

八进制基数为8，数制只使用0、1、2、3、4、5、6、7来表示。

十进制：逢十进一

十进制基数为10，数制只使用0、1、2、3、4、5、6、7、8、9来表示。

十六进制：逢十六进一

十六进制基数为16，数制除了使用0、1、2、3、4、5、6、7、8、9以外，还有用A、B、C、D、E、F来表示10到15。

二.数制之间的相互转换

1.十进制转二进制，八进制，十六进制。（连除法）

1.1十进制转二进制

得出二进制数101101111

1.2十进制转八进制

得出八进制数557

1.3十进制数转十六进制

得出十六进制数16F

2.二进制，八进制，十六进制转十进制。

2.1二进制转十进制

例如：（101101111）2

1*+0*+1*+1*+0*+1*+1*+1*+1*=367

得出十进制是367

2.2八进制转十进制

例如：（557）8

5*+5*+7*=367

得出十进制是367

2.3十六进制转十进制

例如：（16F）16

1*+6*+15*=367

得出十进制是367

3.二进制转八进制八进制，十六进制（分组连乘）

3.1二进制转八进制

得出八进制数557

3.2二进制转十六进制

得出十六进制数是16F

4.八进制，十六进制转二进制（分组连除）

4.1八进制转二进制

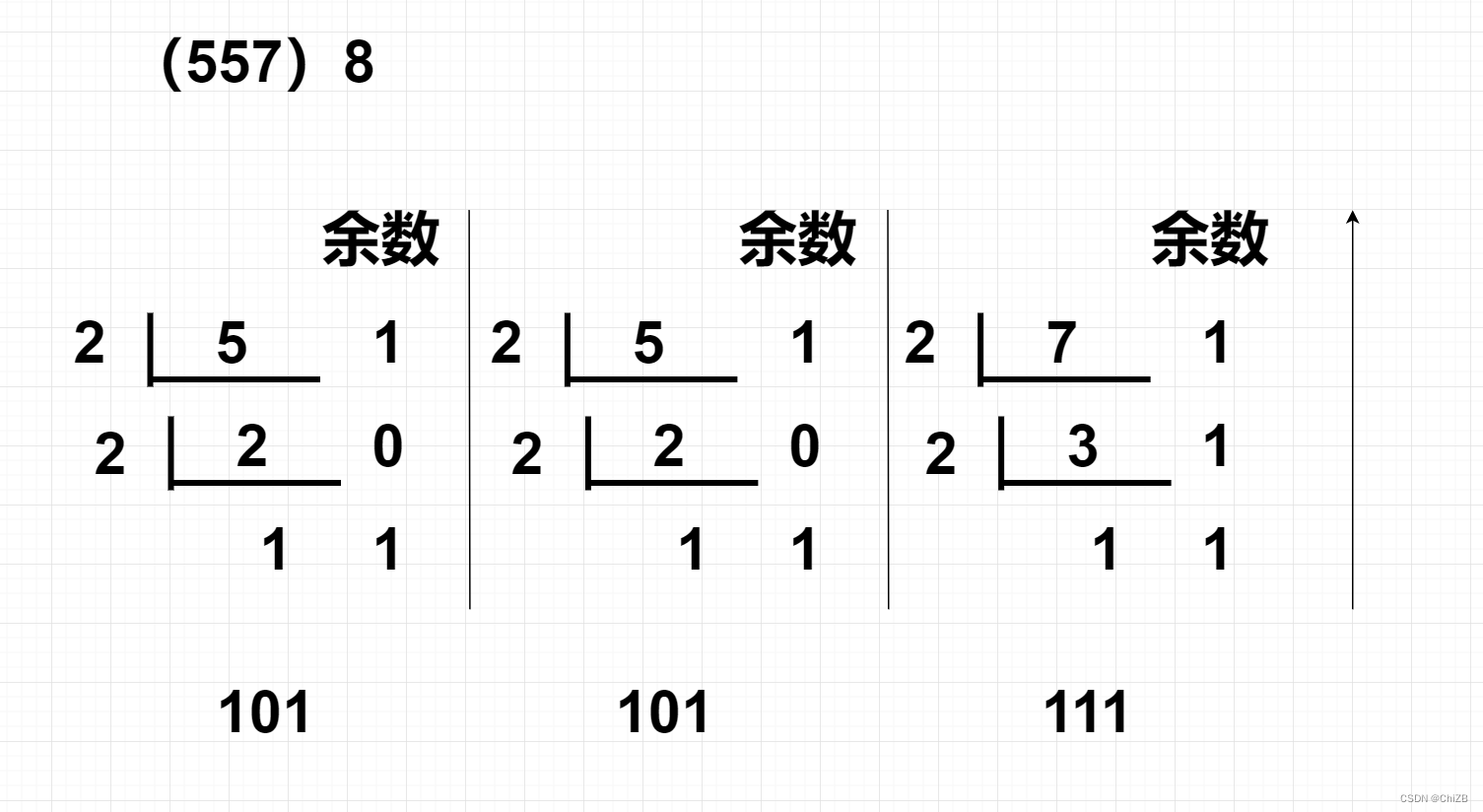
得出二进制数101101111

4.2十六进制转二进制

得出二进制数101101111