最近在做自动泊车项目,利用视觉算法进行车位线检测,其中用到了二维图像坐标与世界坐标的相互转换,因此对相机的标定,相机的位姿计算研究了一番,抽空总结了一下,分享给广大网友。
在图像测量过程以及机器视觉应用中,为确定空间物体表面某点的三维几何位置与其在图像中对应点之间的相互关系,必须建立相机成像的几何模型,这些几何模型参数就是相机参数。在大多数条件下这些参数必须通过实验与计算才能得到,这个求解参数(内参、外参、畸变参数)的过程就称之为相机标定(或摄像机标定)。无论是在图像测量或者机器视觉应用中,相机参数的标定都是非常关键的环节,其标定结果的精度及算法的稳定性直接影响相机工作产生结果的准确性。因此,做好相机标定是做好后续工作的前提,提高标定精度是科研工作的重点所在。
畸变(distortion)是对直线投影(rectilinear projection)的一种偏移。简单来说直线投影是场景内的一条直线投影到图片上也保持为一条直线。畸变简单来说就是一条直线投影到图片上不能保持为一条直线了,这是一种光学畸变(optical aberration),可能由于摄像机镜头的原因。
坐标转换基础
在视觉测量中,需要进行的一个重要预备工作是定义四个坐标系的意义,即世界坐标系(参考坐标系)、摄像机坐标系 、 图像物理坐标系和像素坐标系。
(1)世界坐标系就是物体在真实世界中的坐标,比如黑白棋盘格的世界坐标系原点定在第一个棋盘格的顶点,Xw,Yw,Zw互相垂直,Zw方向就是垂直于棋盘格面板的方向。可见世界坐标系是随着物体的大小和位置变化的,单位是长度单位。只要棋盘格的大小决定了,无论板子怎么动,棋盘格角点坐标一般就不再变动(因为是相对于世界坐标系原点的位置不变),且认为是Zw=0。
(2)相机坐标系以光心为相机坐标系的原点,以平行于图像的x和y方向为Xc轴和Yc轴,Zc轴和光轴平行,Xc,Yc,Zc互相垂直,单位是长度单位。
(3)图像物理坐标系以主光轴和图像平面交点为坐标原点,x和y方向如图所示,单位是长度单位。
(4)图像像素坐标系以图像的顶点为坐标原点,u和v方向平行于x和y方向,单位是以像素计。
针孔相机的模型:三维世界中的物体,经过相机成像系统,变成二维图像过程如下所示。
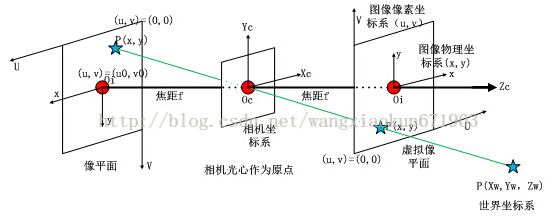
1.世界坐标系通过外参矩阵转换到相机坐标系(刚体变换和平移)
空间中一点的世界坐标为:
[
X
w
,
Y
w
,
Z
w
]
T
[Xw,Yw,Zw]^T
[Xw,Yw,Zw]T,当把它转换到相机坐标系的时候,先把它加一维用齐次坐标来表示它(这样就方便对它本身进行平移操作)。左乘一个3x4的外参矩阵,从世界坐标系转换到相机坐标系。
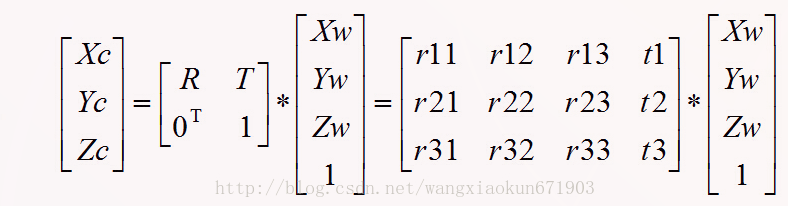
[
X
c
,
Y
c
,
Z
c
]
T
[Xc,Yc,Zc]^T
[Xc,Yc,Zc]T表示相机坐标,
[
X
w
,
Y
w
,
Z
w
]
T
[Xw,Yw,Zw]^T
[Xw,Yw,Zw]T表示物体所在的世界坐标,R是旋转矩阵(3个自由度),T是平移矩阵,两者组成3×4矩阵即为相机的外参矩阵。
采用opencv进行相机标定,求出的外参是旋转向量,旋转向量和旋转矩阵两者之间可以通过罗德里格斯(Rodrigues)变换来进行转换。
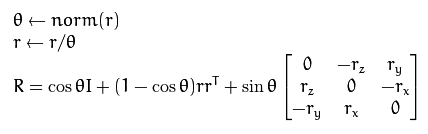
其中,旋转向量的长度(模)表示绕轴逆时针旋转的角度(弧度),norm为求向量的模。反变换也可以很容易的通过如下公式实现:
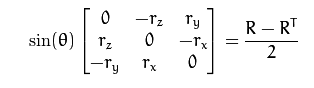
2.相机坐标系通过内参矩阵转换到图像像素坐标系
这一步是经过两步实现的,一般情况下,相机成像过程中都会存在畸变,因此在标定的过程中需要求取畸变系数。
2.1 畸变
畸变一般可以分为:径向畸变、切向畸变

其中,k1,k2,k3径向畸变系数,p1,p2是切向畸变系数。畸变发生在相机坐标系转图像物理坐标系的过程中。操作的对象是相机坐标系。
这一步是加入畸变的过程,如果忽略这一步,考虑理想情况下的话,可以直接跳到下一步。
2.2 相机坐标系通过焦距对角矩阵和畸变系数转换到图像物理坐标系
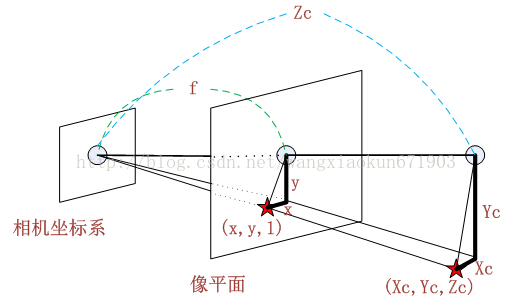
由相似三角形可得:

f表示焦距,
[
X
c
,
Y
c
,
Z
c
]
T
[Xc,Yc,Zc]^T
[Xc,Yc,Zc]T表示相机坐标。
[
x
,
y
,
1
]
T
[x,y,1]^T
[x,y,1]T表示归一化后的图像物理坐标。若考虑畸变,则公式中的
[
X
c
,
Y
c
,
Z
c
]
T
[Xc,Yc,Zc]^T
[Xc,Yc,Zc]T为上述加入畸变系数后所求的值。
2.3 图像物理坐标系通过像素转换矩阵转换到像素坐标系中
这一步是在同一个平面上做的,只不过是先换了表示单位,又换了坐标原点的位置。

dx和dy表示:x方向和y方向的一个像素分别占多少个(可是小数)长度单位。u0,v0表示图像的中心像素坐标和图像原点像素坐标之间相差的横向和纵向像素数。
3.转换过程总公式






















 1813
1813











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








