查找之B树，B+树，B*树及分析MySQL的两种引擎

最新推荐文章于 2024-03-06 23:32:37 发布

杰哥一号号

最新推荐文章于 2024-03-06 23:32:37 发布

阅读量274

点赞数

分类专栏：算法文章标签：查找 B树

算法专栏收录该内容

21 篇文章 0 订阅

订阅专栏

接触到了数据结构当中的B树，B+树，B*树，我觉得应该写一篇博客记录下，毕竟是第一次接触的，只有写了博客以后，感觉对这个的印象才会更加深刻。
前言：
为什么要有B树？
学习任何一个东西我们都要知道为什么要有它，B树也一样，既然存储数据，我们为什么不用红黑树呢？

这个要从几个方面来说了，
计算机有一个局部性原理，就是说，当一个数据被用到时，其附近的数据也通常会马上被使用。
所以当你用红黑树的时候，你一次只能得到一个键值的信息，而用B树，可以得到最多M-1个键值的信息。这样来说B树当然更好了。
另外一方面，同样的数据，红黑树的阶数更大，B树更短，这样查找的时候当然B树更具有优势了，效率也就越高。

一.B树

首先我们来谈一谈关于B树的问题，

对于B树，我们首先要知道它的应用，B树大量应用在数据库和文件系统当中。

B树是对二叉查找树的改进。它的设计思想是，将相关数据尽量集中在一起，以便一次读取多个数据，减少硬盘操作次数。

B树为系统最优化大块数据的读和写操作。B树算法减少定位记录时所经历的中间过程，从而加快存取速度。普遍运用在数据库和文件系统。

假定一个节点可以容纳100个值，那么3层的B树可以容纳100万个数据，如果换成二叉查找树，则需要20层！假定操作系统一次读取一个节点，并且根节点保留在内存中，那么B树在100万个数据中查找目标值，只需要读取两次硬盘。

B 树可以看作是对2-3查找树的一种扩展，即他允许每个节点有M-1个子节点。

B树的结构要求：
1）根节点至少有两个子节点
2）每个节点有M-1个key，并且以升序排列
3）位于M-1和M key的子节点的值位于M-1 和M key对应的Value之间
4）其它节点至少有M/2个子节点
5）所有叶子节点都在同一层
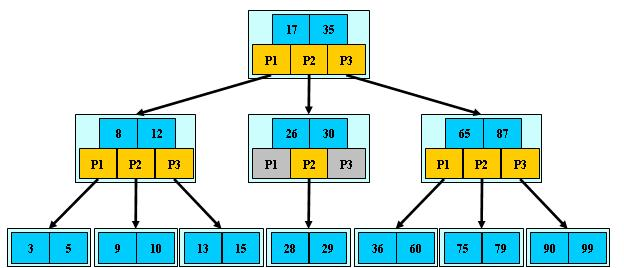
这里写图片描述
根据B树的特点，我们首先可以写出B树的整体的结构。

1.B树结构

 B树的结构我们定义需要参考规则，我们首先是需要给出保存键值的一个数组，这个数组的大小取决与我们定义的M，然后我们根据规则，可以得到一个保存M+1个子的一个数组，然后当然为了方便访问，parent指针，然后要有一个记录每个节点中键值个数的一个size。

所以定义如下：

 
 1
2
3
4

template <typename K,int M>
struct BTreeNode
{
    K _keys[M];                     //用来保存键值。
    BTreeNode<K, M>* _sub[M + 1];   //用来保存子。
    BTreeNode<K, M>* _parent;
    size_t _size;
    BTreeNode()
        :_parent(NULL)
        , _size(0)
    {
        int i = 0;
        for ( i = 0; i < M; i++)
        {
            _keys[i] = K();
            _sub[i] = K();
        }
        _sub[i] = K();
    }
};

 
 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

2.B树的查找

对于AVL，BST，红黑树，B树这些高级的数据结构而言，查找算法是非常重要的。我们首先确定返回值，对于这种关于key和key-value的数据结构，参考map和set，我们让它返回一个pair的一个结构体。
pair结构体的定义在std中是

template<typename K,typename V>
struct pair
{
    K key;
    V value;
}
 
 1
2
3
4
5
6

我们只需要让这个里面的value变为bool值，value返回以后说明的是存不存就可以了。

接下来的思路就是从根节点进行和这个节点当中的每一个key比较，如果=那么就返回找到了，如果小于，那么就到这个节点左面的子节点中找，如果大了，就继续向后面的键值进行查找。如果相等那么就返回。

示例代码：

pair <Node*,int > Find(const K &key)
    {
        Node* cur = _root;
        Node* parent = NULL;
        while (cur)
        {
            size_t i = 0;
            while (i < cur->_size)
            {
                //如果小于当前，向后
                if (cur->_keys[i] < key)
                {
                    i++;
                }
                //如果大于，
                else if (cur->_keys[i]>key)
                {
                    cur = cur->_sub[i];
                    parent = cur;
                    break;
                }
                //相等，返回这个节点
                else
                {
                    return pair<Node *, int>(NULL, -1);
                }

            }
            if (key > cur->_sub[i + 1])
            {
                cur = cur->_sub[i];
            }

            //为了防止出现我返回空指针操作，如果是空指针，那么就返回父亲
            if (cur != NULL && i == cur->_size)
            {
                parent = cur;
                cur = cur->_sub[i];
            }

        }
        return pair<Node *, int>(parent, 1);

    }
 
 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44

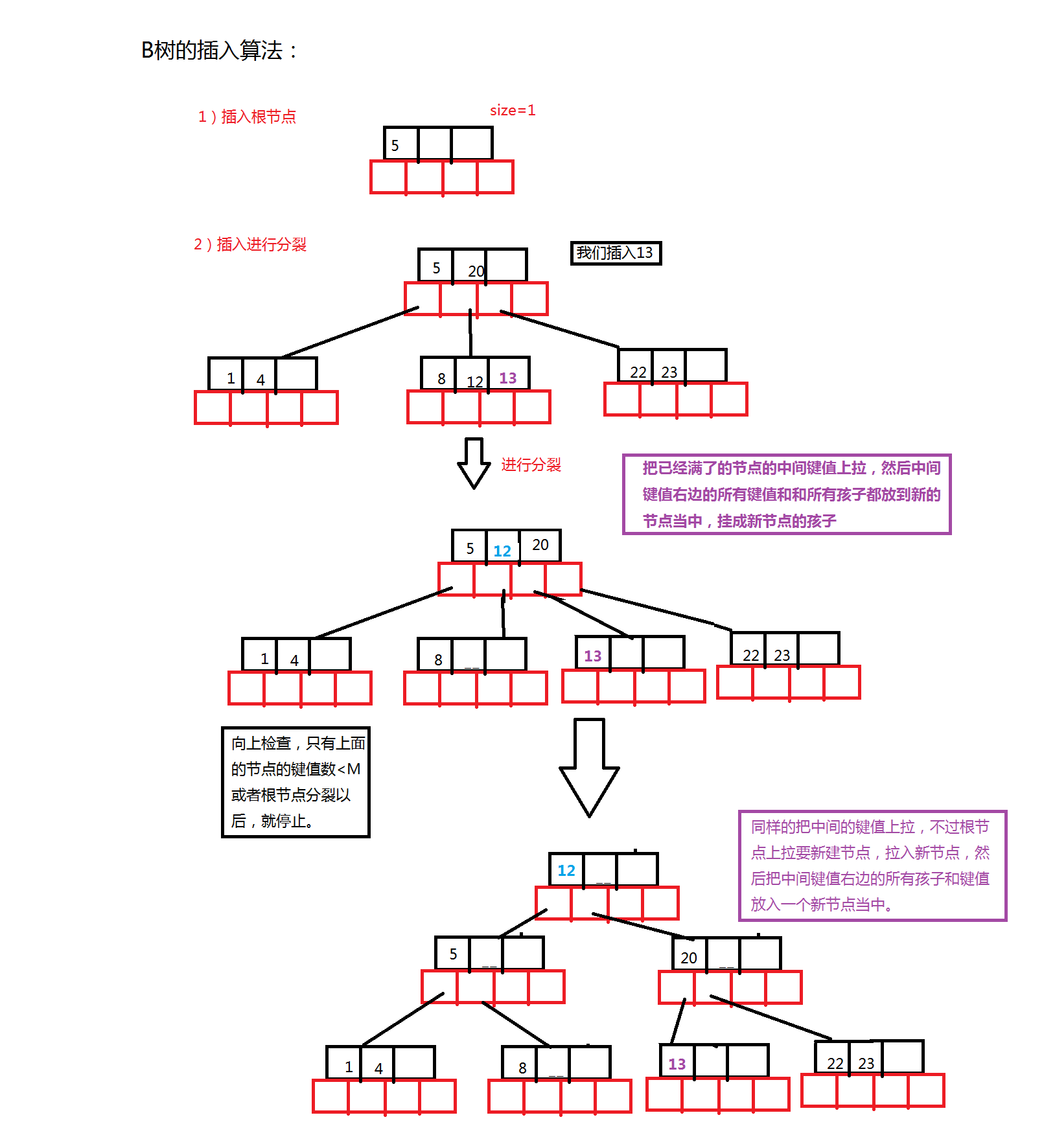
3.B树的插入

这里写图片描述
示例代码：


    bool Insert(const K &key)
    {
        //首先来考虑空树的情况
        if (_root == NULL)
        {
            //给这个节点中添加key，并且让size++。
            _root = new Node;
            _root->_keys[0] = key;
            _root->_size++;
            return true;
        }
        //使用通用的key-value结构体来保存找到的key所在的节点。

        pair<Node*,int > ret=Find(key);

        //在这里来看这个节点是否存在，存在就直接return false。
        if (ret.second == -1)
        {
            return false;
        }

        Node* cur = ret.first;
        K newKey = key;
        Node *sub = NULL;
        //此时表示考虑插入。
        while (1)
        {
            //向cur里面进行插入，如果没满插入，满了就进行分裂。
            InsetKey(cur, newKey, sub);

            //小于M，这样就可以直接插入
            if (cur->_size < M)
            {
                return true;
            }

            //如果==M，那么就应该进行分裂
            //首先找到中间的节点
            size_t mid = cur->_size / 2;
            //创建一个节点，用来保存中间节点右边所有的节点和子节点。
            Node * tmp = new Node;

            size_t j = 0;
            //进行移动sub以及所有的子接点。
            for (size_t i = mid + 1; i < cur->_size; i++)
            {
                tmp->_keys[j] = cur->_keys[i];
                cur->_keys[i] = K();
                cur->_size--;
                tmp->_size++;
                j++;
            }

            //移动子串
            for (j = 0; j < tmp->_size + 1; j++)
            {
                tmp->_sub[j] = cur->_sub[mid + 1 + j];
                if (tmp->_sub[j])
                {
                    tmp->_sub[j]->_parent = tmp;
                }
                cur->_sub[mid + 1 + j] = NULL;
            }



            //进行其他的移动
            //分裂的条件就是要么分裂根，要么就是分裂子节点，要么就是所在节点的节点数小于M。

            //考虑根分裂，分裂的时候创建节点，然后把中间节点上拉，记得要更改最后的parent
            if (cur->_parent == NULL)
            {
                _root = new Node();
                _root->_keys[0] = cur->_keys[mid];
                cur->_keys[mid] = K();
                cur->_size--;
                _root->_size++;

                _root->_sub[0] = cur;
                cur->_parent = _root;

                _root->_sub[1] = tmp;
                tmp->_parent = _root;
                return true;
            }
            //分裂如果不是根节点，那么就把mid节点插入到上一层节点中，然后看上一层节点是否要分裂。注意修改cur和sub

            else
            {
                newKey = cur->_keys[mid];
                cur->_keys[mid] = K();
                cur->_size--;
                cur = cur->_parent;

                sub = tmp;
                sub->_parent = cur;

            }
        }

    }
    void InsetKey(Node* cur, const K &key, Node* sub)
    {
        int i = cur->_size - 1;
        while (i>=0)
        {
            //进行插入
            if (key > cur->_keys[i])
            {
                break;
            }
            //进行移动
            else
            {
                cur->_keys[i + 1] = cur->_keys[i];
                cur->_sub[i + 2] = cur->_sub[i + 1];
            }
            i--;
        }
        //进行插入
        cur->_keys[i + 1] = key;
        //插入子
        cur->_sub[i + 2] = sub;

        //如果没满，只需要对size++；
        if (cur->_size < M)
        {
            cur->_size++;
        }
    }
 
 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131

二.B+树

接下来介绍B树的升级版本，

B+树
B+树是B-树的变体，也是一种多路搜索树：
1.其定义基本与B-树同，除了：
2.非叶子结点的子树指针与关键字个数相同；
3.非叶子结点的子树指针P[i]，指向关键字值属于[K[i], K[i+1])的子树（B-树是开区间）；
5.为所有叶子结点增加一个链指针；
6.所有关键字都在叶子结点出现；
这里写图片描述

B+树相比于B树能够更加方便的遍历。

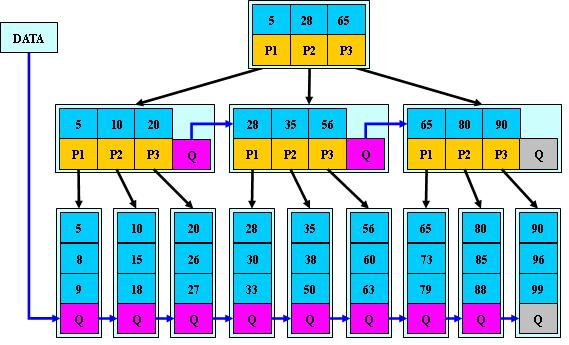
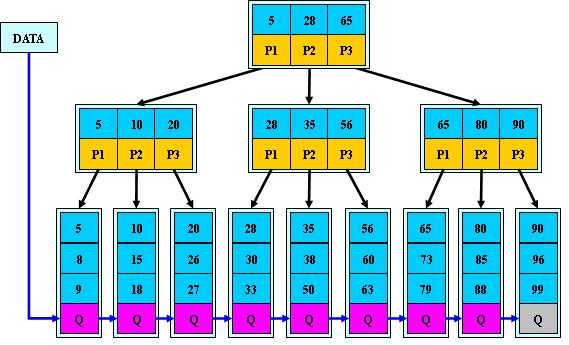
B+树简单的说就是变成了一个索引一样的东西。 B+的搜索与B-树也基本相同，区别是B+树只有达到叶子结点才命中（B-树可以在非叶子结点命中），B+树的性能相当于是给叶子节点做一次二分查找。

B+树只有叶子节点存的是Key-value，非叶子节点只需要存储key就好了。

B+树的查找算法：当B+树进行查找的时候，你首先一定需要记住，就是B+树的非叶子节点中并不储存节点，只存一个键值方便后续的操作，所以非叶子节点就是索引部分，所有的叶子节点是在同一层上，包含了全部的关键值和对应数据所在的地址指针。这样其实，进行 B+树的查找的时候，只需要在叶子节点中进行查找就可以了。

B+树的插入算法与B树的大致思想也是一样的，只不过在这里的上拉就是只把键值上拉。

三.B*树

接下来要说明的就是B*树，B*树是对B+树进行的又一次的升级。在B+树的非根和非叶子结点再增加指向兄弟的指针；

这里写图片描述
在B+树基础上，为非叶子结点也增加链表指针，将结点的最低利用率从1/2提高到2/3；

在这比如说当你进行插入节点的时候，它首先是放到兄弟节点里面。如果兄弟节点满了的话，进行分裂的时候从兄弟节点和这个节点各取出1/3，放入新建的节点当中，这样也就实现了空间利用率从1/2到1/3。

四.关于B树和B+树相关应用拓展

其实B树B+树最需要关注的是它们的应用，B树和B+树经常被用于数据库中，作为MySQL数据库索引。索引（Index）是帮助MySQL高效获取数据的数据结构。

为了查询更加高效，所以采用B树作为数据库的索引。
在MySQL中，索引属于存储引擎级别的概念，不同存储引擎对索引的实现方式是不同的，我们接下来讨论两个引擎：MyISAM和InnoDB这两种引擎。

1.MyISAM

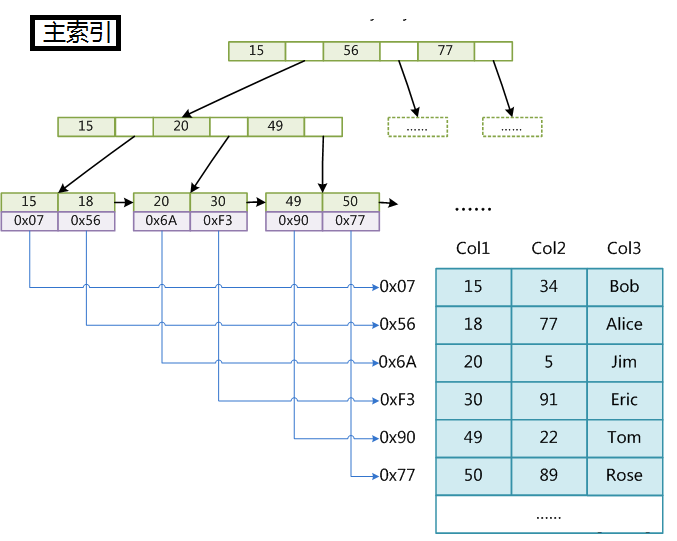
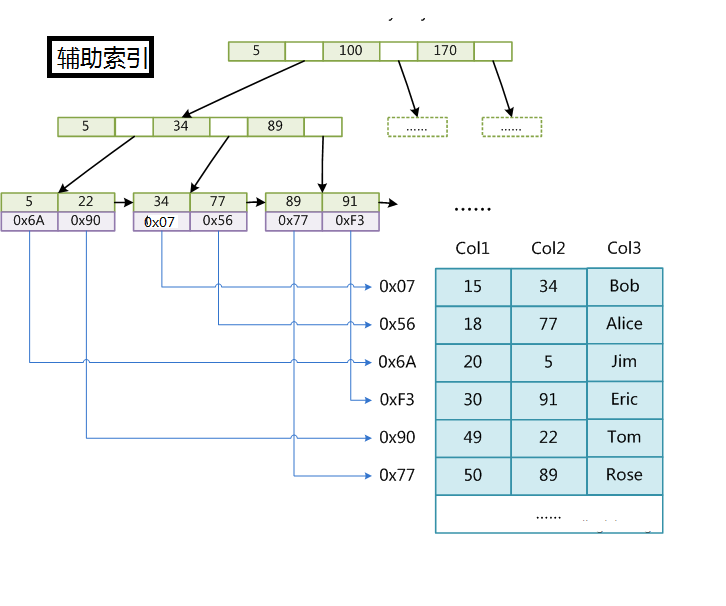
这里写图片描述

MyISAM中有两种索引，分别是主索引和辅助索引，在这里面的主索引使用具有唯一性的键值进行创建，而辅助索引中键值可以是相同的。MyISAM分别会存一个索引文件和数据文件。它的主索引是非聚集索引。当我们查询的时候我们找到叶子节点中保存的地址，然后通过地址我们找到所对应的信息。

2.InnoDB

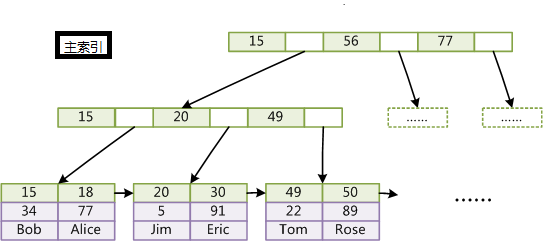
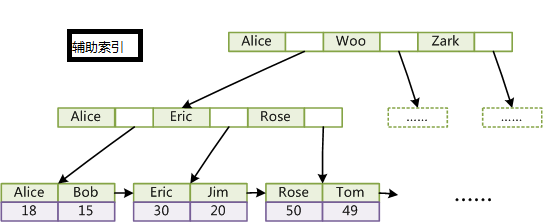
这里写图片描述

InnoDB索引和MyISAM最大的区别是它只有一个数据文件，在InnoDB中，表数据文件本身就是按B+Tree组织的一个索引结构，这棵树的叶节点数据域保存了完整的数据记录。所以我们又把它的主索引叫做聚集索引。而它的辅助索引和MyISAM也会有所不同，它的辅助索引都是将主键作为数据域。所以，这样当我们查找的时候通过辅助索引要先找到主键，然后通过主索引再找到对于的主键，得到信息。

这就是MySQL的两种引擎
这两种引擎那个好呢？

从历史上来说MyISAM历史更加久远，所以InnoDB性能也就更好了，在这我们需要考虑当我们修改数据库中的表的时候，数据库发生了变化，那么他们的主键的地址也就发生了变化，这样你的MyISAM的主索引和辅助索引就需要进行重新建立索引。而InnoDB只需要改变主索引，因为它的辅助索引是存主键的。所以这样考虑InnoDB更加高效。

另外，我们也就很容易明白为什么不建议使用过长的字段作为主键，因为所有辅助索引都引用主索引，过长的主索引会令辅助索引变得过大。