B+树完全解析

一、B+树的结点组成

B+树包含两种结点：

0、根结点：(一般区分为两种，这里我将根结点分开说明，因为根节点非常特殊而且唯一)

      若树只有一层：仅有根结点，此根结点也是叶结点，根结点中索引值个数无最少限制。

      若树为两层以及以上：最上面那一层为根结点，根结点属于内部结点，根节点中指针最少为2个。

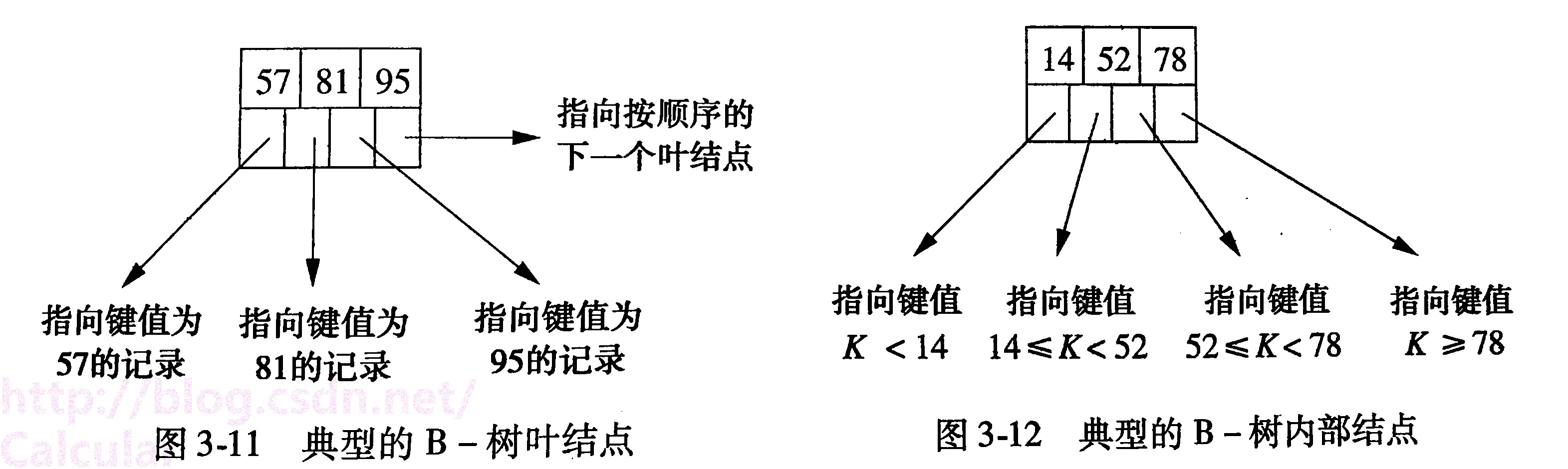
1、叶结点：叶节点在B+树的最底层（所有叶节点都在一层），叶结点中存放索引值、指向记录的指针、指向下一个叶结点的指针。叶结点内的索引值是记录中键的拷贝，这些索引值以排好序的形式，从左到右分布在叶节点中。

2、内部结点：所有非叶结点都属于内部结点，所有内部结点上的索引值都是叶结点的副本。内部结点中存放索引值、指向某一个结点（可以是叶结点也可以是内部节点）的指针。

这两种节点的构成直观图如下：    （可以看到两者的存储空间是一样的）

二、B+树的结构，结点的合法性

B+树必然是平衡的，从树根到树叶的所有路径都是等长的。

不同格式的B+树的区别仅有唯一参数n，n为树中所有结点（无论叶结点还是内部结点）包含的指针数目。

在上图中我们可以看出，n为4。

一旦n确定下来，在整个操作过程中都不会变，在整个操作过程中，任何结点的占用空间均为：

n-1个索引值空间 + n个指针空间

事实上，在文件系统中，每个物理块都代表一个结点（可能有未被利用的空间，但要保证能放下一个结点，且n尽可能大）

在树高度大于等于2层时，若结点是合法的，则有如下：

0.对于根节点：存放指针的空间只需 >= 2 即可。

1.对于内部结点：存放指针空间的装满量必须 >= 一半，在上图中，n=4因此必须存放2~4个指针才算合法。

2.对于叶结点：存放指向记录的指针的装满量必须 >= 一半。注意！存放记录的指针量是n-1，有1个是指向下一个叶结点的指针，因此当n=4时，存放记录的指针个数为2或3时都是合法的。

3.叶节点每一个索引值对应一个记录指针。内部结点每一个索引值划分两个区间，并把区间对应到指针上，因此若内部结点有a个索引，指针需要a+1个。

4.索引值不重复（这里不讨论索引值重复的变体）

对于高度仅为1的树，没有上述要求（因为最开始单个节点中肯定没有东西）

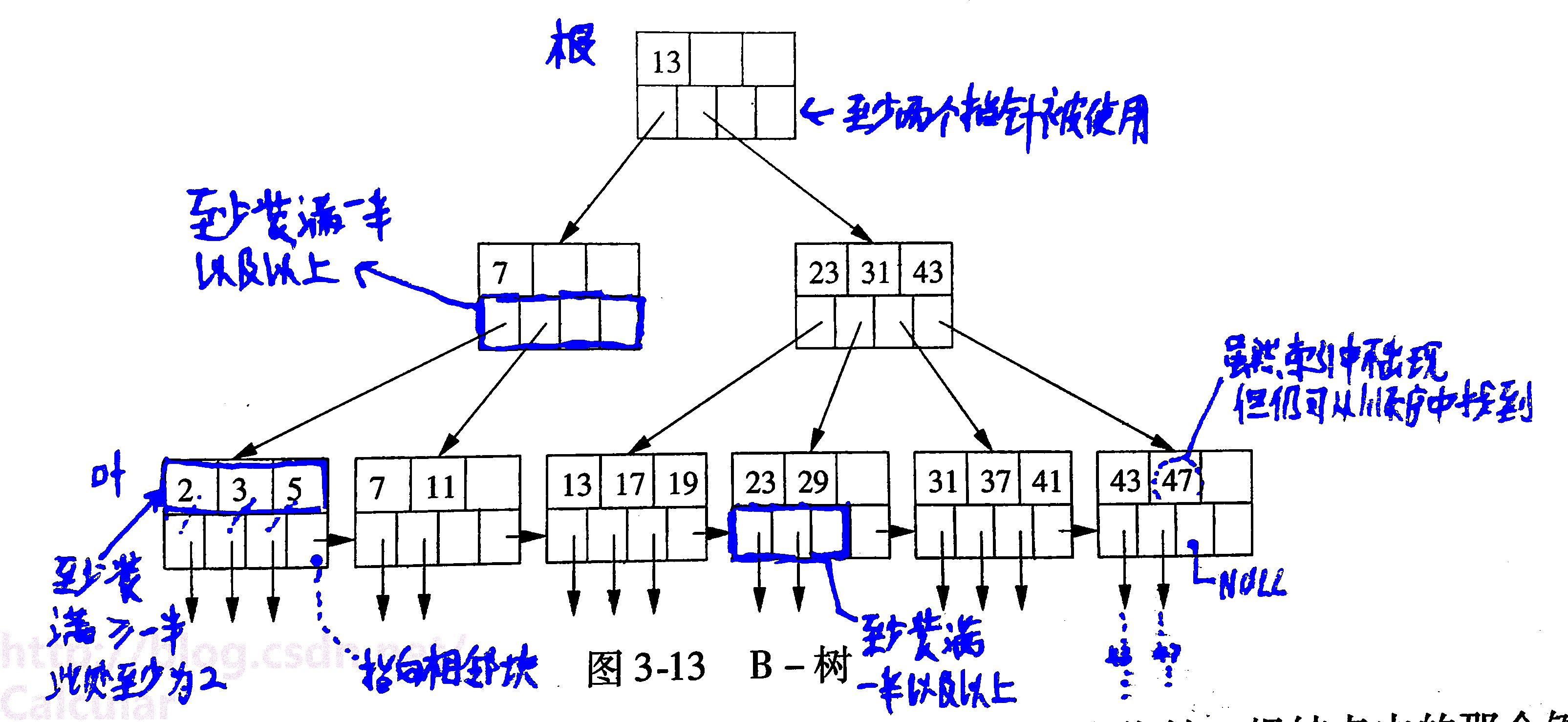
一颗棵合法的B+树可能有如下形状：

三、B+树的查找

从根结点开始，首先从结点内部查找（由于结点内部是升序的，二分查找即可）

比如查找4，结点内部存放1,5,8,3 那么查到5就可以停了，沿着对应的5左边的指针（区间1<=x<5）继续向下查找

直到最后进入叶节点。

若叶节点中存在该索引值，就能找到对应记录的指针，若不存在，则查找失败

四、B+树的插入

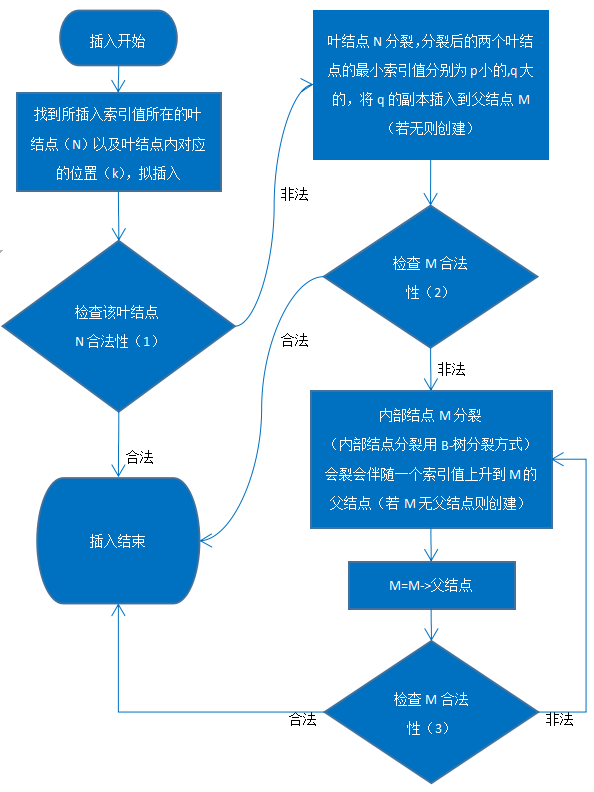
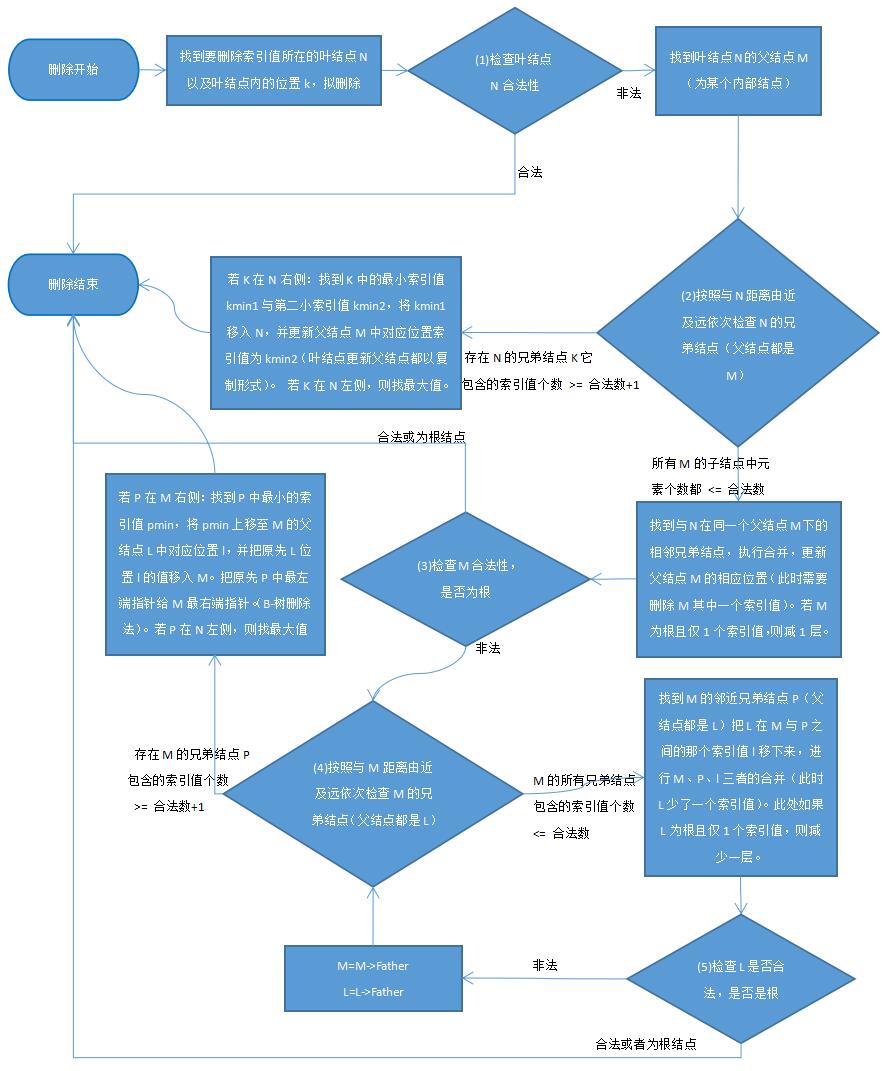
B+树插入流程图：

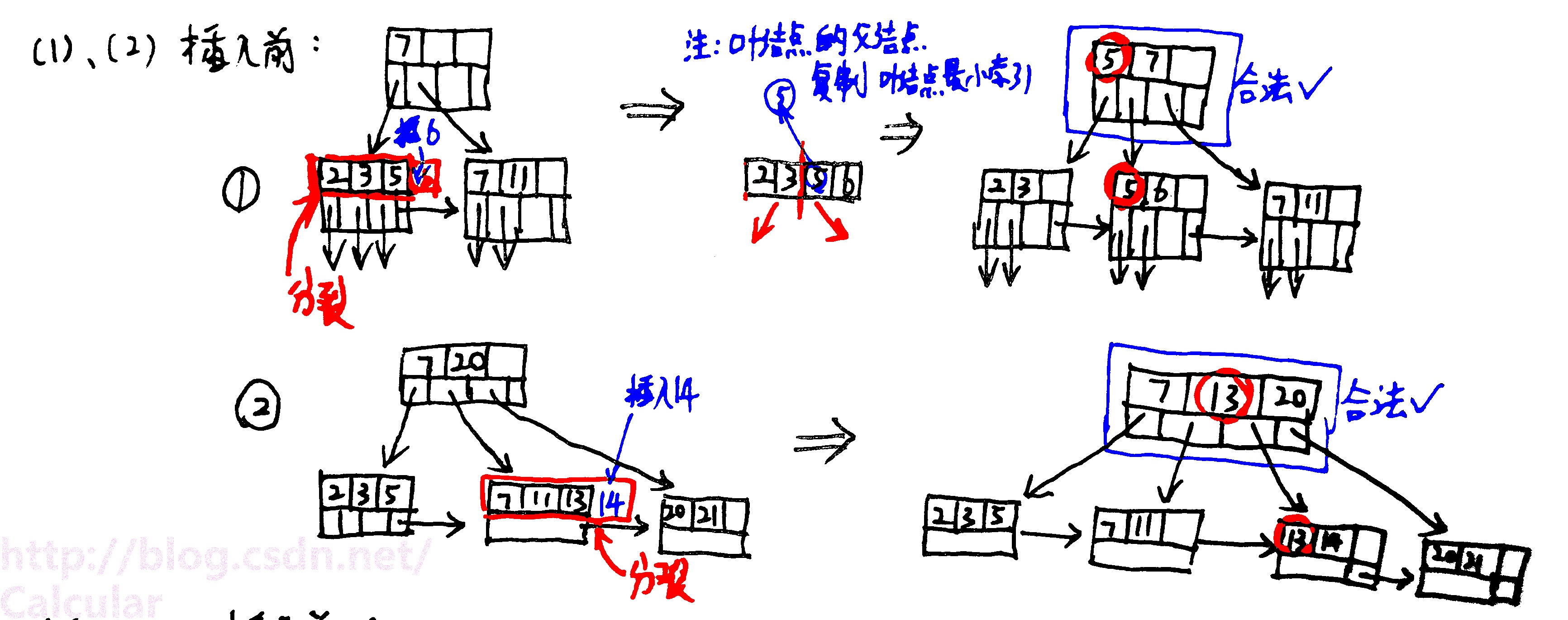
经过（1）的插入：

经过（1）、（2）的插入：

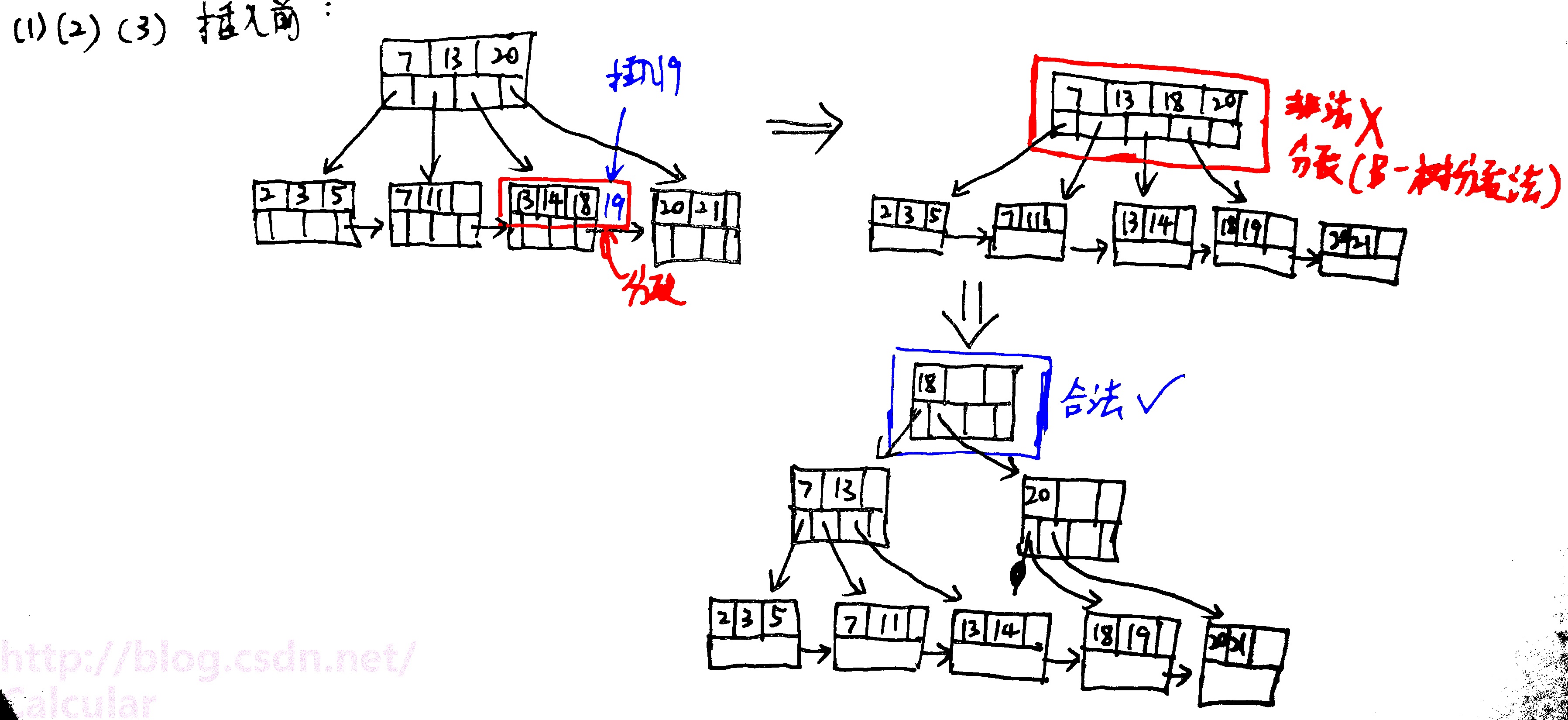
经过（1）、（2）、（3）的插入：

五、B+树删除

相比插入，删除过程更为复杂：

经过（1）删除：

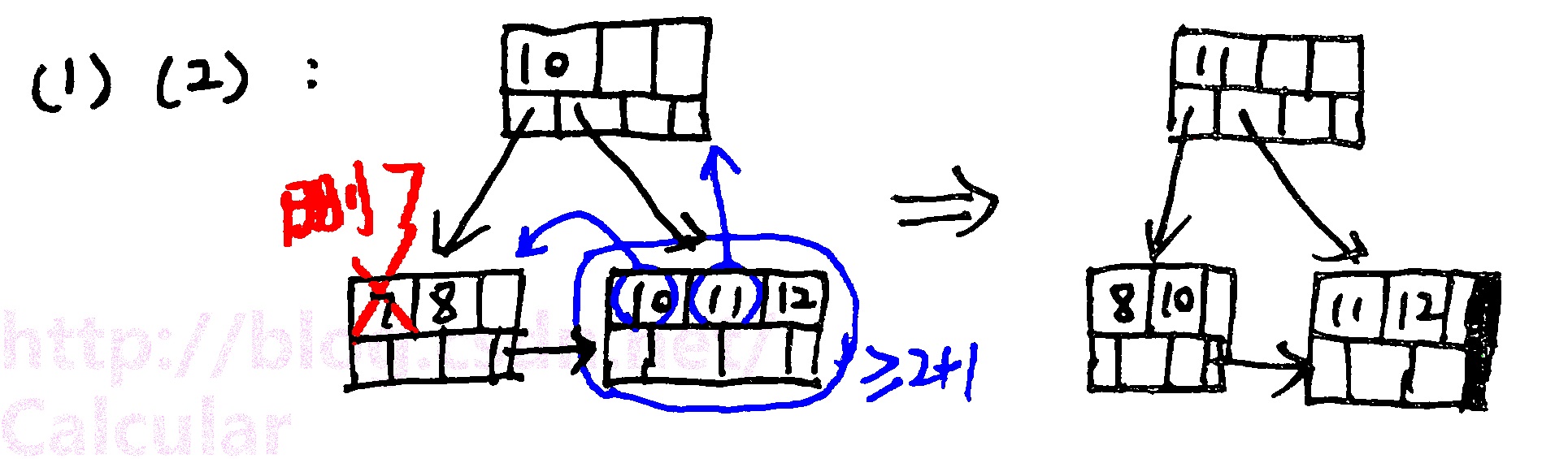
经过（1）、（2）删除：

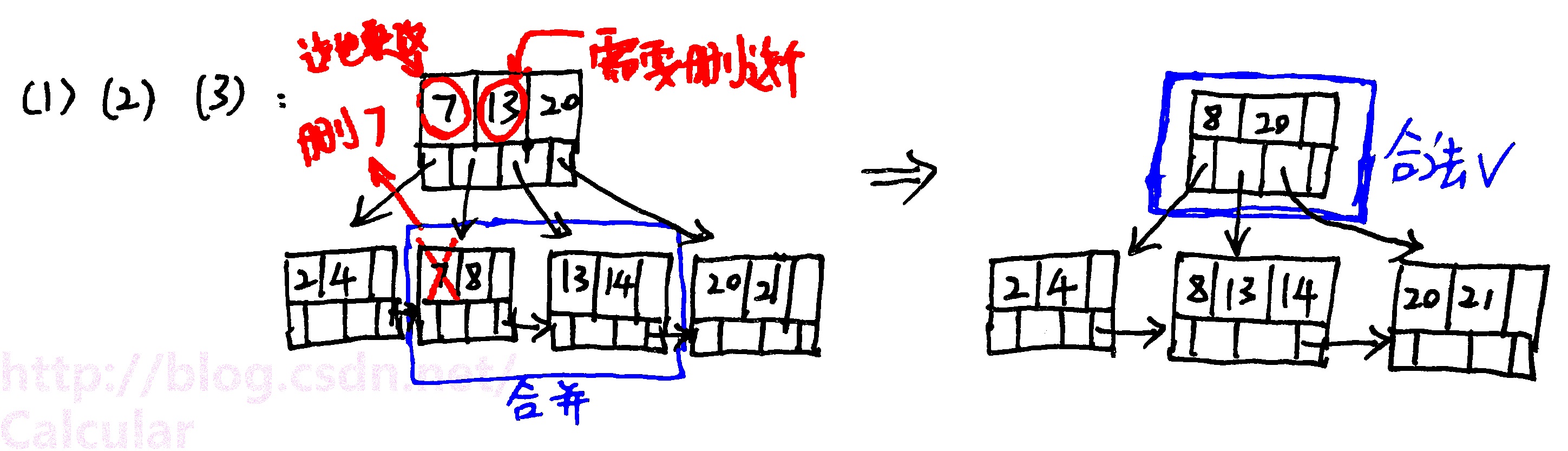
经过（1）、（2）、（3）删除：

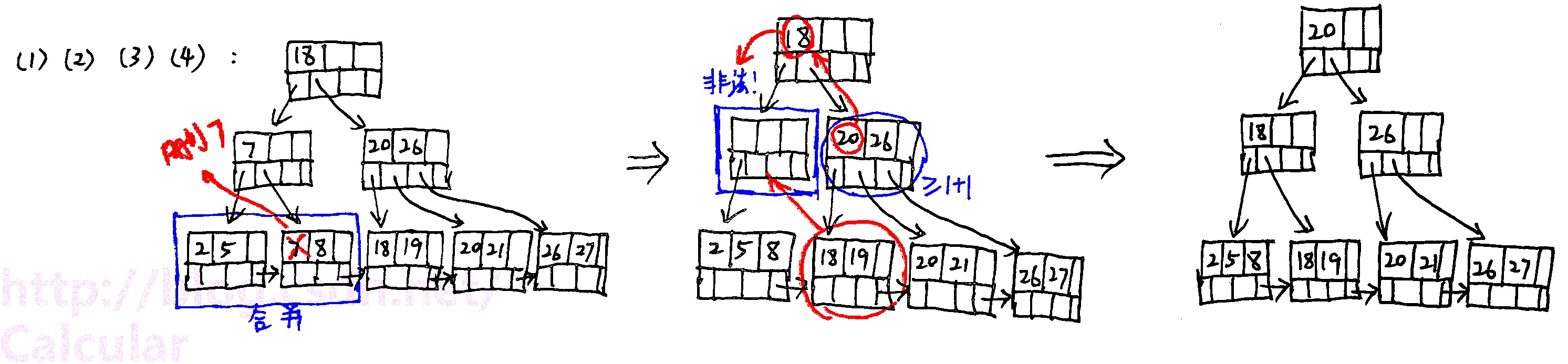
经过（1）、（2）、（3）、（4）删除：

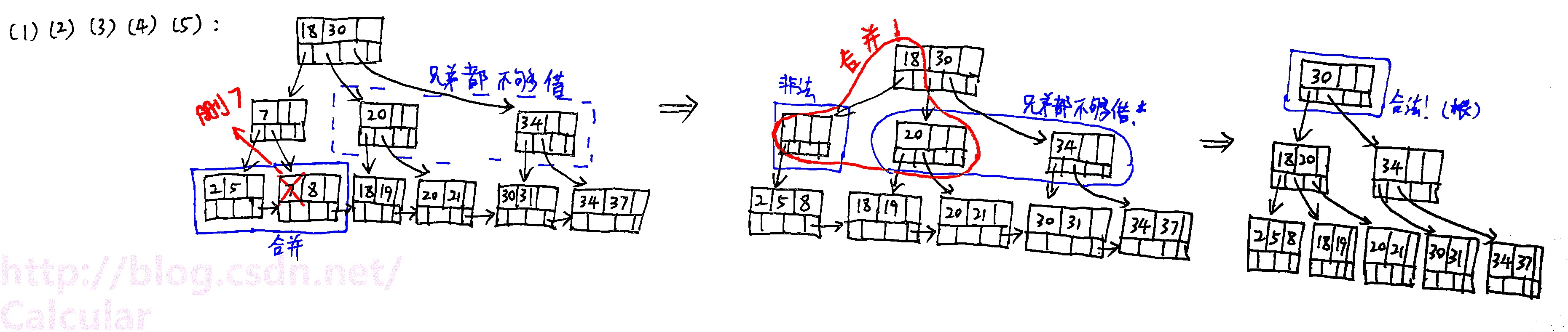
经过（1）、（2）、（3）、（4）、（5）删除：

例题：

Given the following 2-gram search keys:

(A,5), (D,3), (D,7), (H,5), (K,1), (N,1), (P,2), (Q,3), (X,1), (X,2)

Please construct a B+ tree, which each node can hold 4 pointers and 3 search keys.

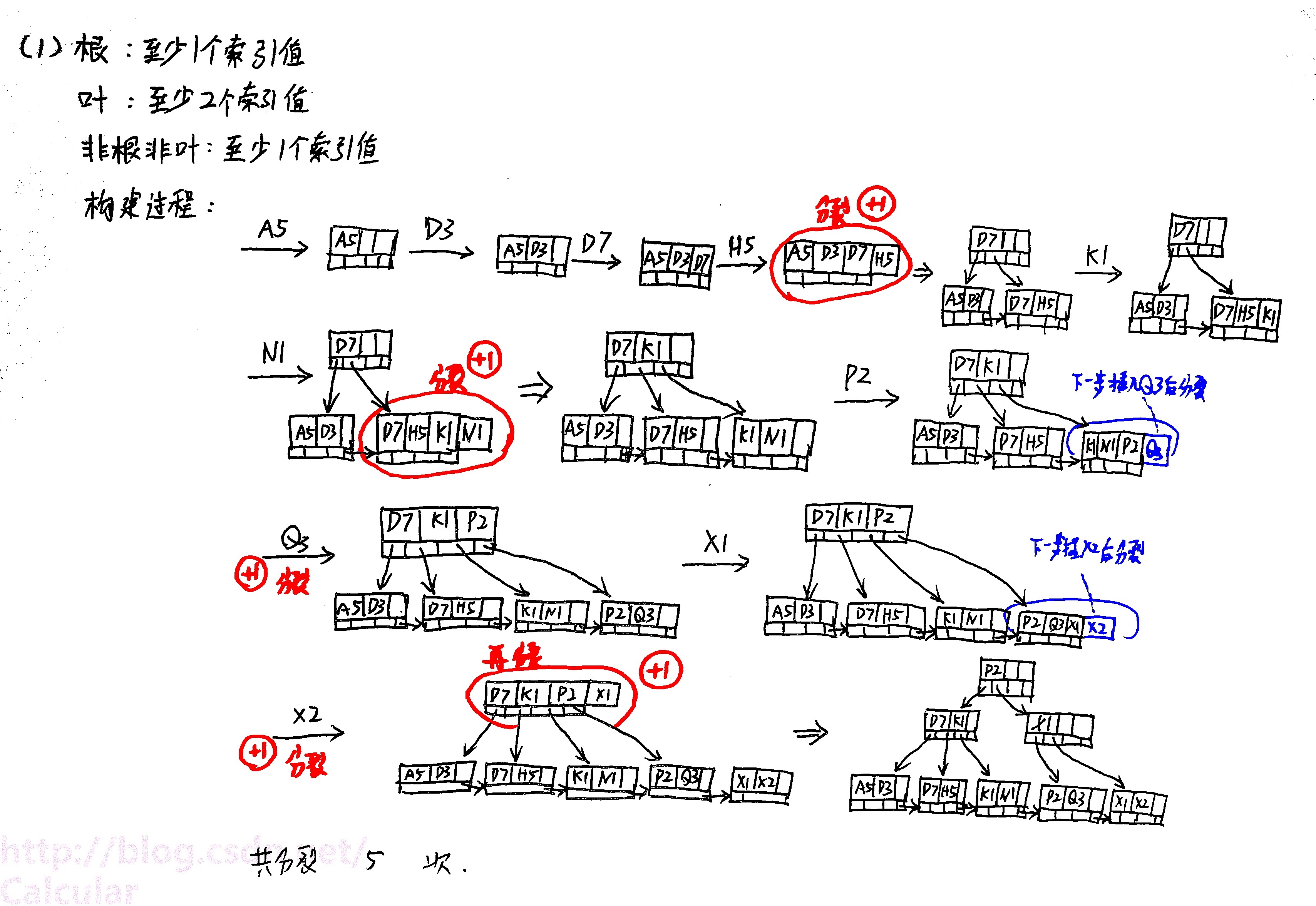
(1) How many search key can a root node, a non-root & non-leaf node, or a leaf node at least hold ? How many times of splitting during the construction of the B+ tree?

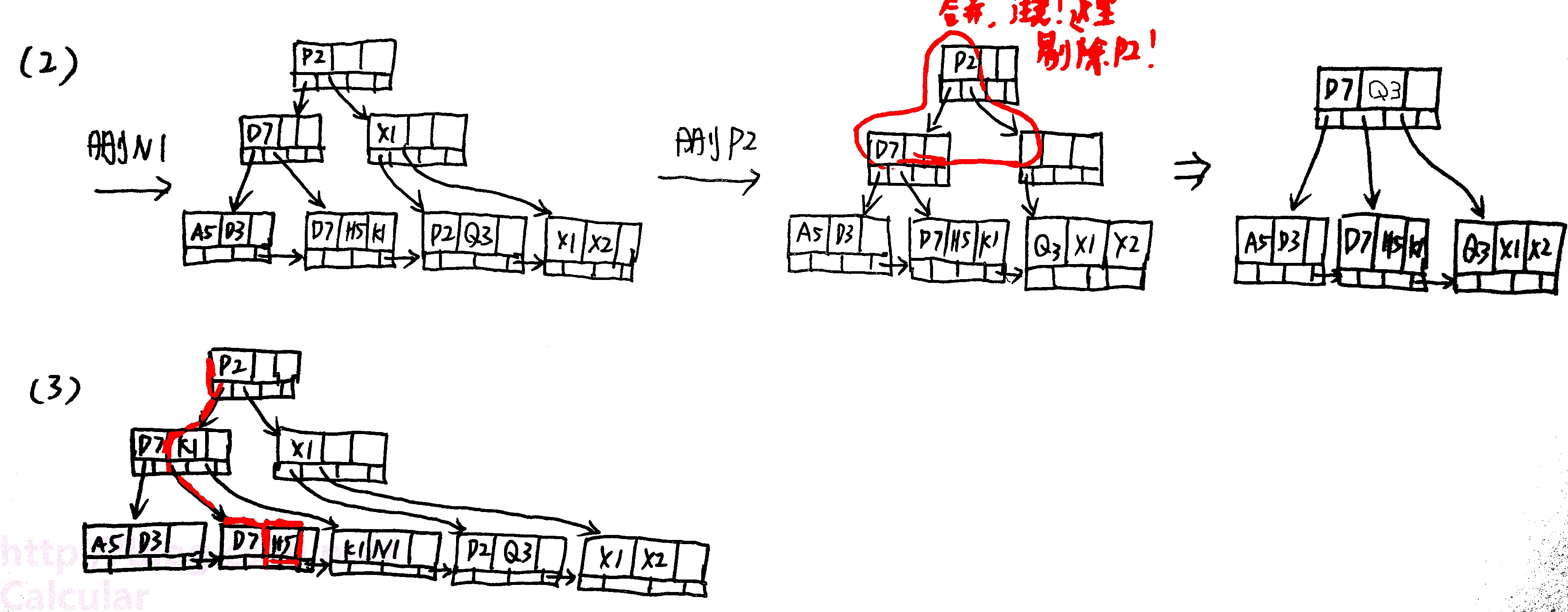
(2) Please give the B+ tree after deleting (N,1) and (P,2).

(3) Please describe the process of searching keys that are greater than (D,8), and not equals to (H,8).

例题解答：

此题涉及的就是B+树的结构以及操作。

(1) 问：B+树种一个结点能容纳4个指针和3个索引值（查找键），分别说出根、叶、非根非叶的结点至少有多少索引值，在上述序列插入过程中，会分裂多少次。

 

(2) 问：给出删除N1和P2后的树。

(3) 问：描述查找大于D8小于H8索引值的过程。