平衡二叉树(Balanced Binary Tree)是二叉树的一个进化体,由于它是由G.M. Adelson-Velsky 和 E.M. Landis于1962年发明的,因此也被称为
AVL树。AVL-Tree是指在一棵树中任意一个节点其左右子树的高度差最多为1。一个节点的左右子树高度差称之为该节点的平衡因子。AVL-Tree
经常被用于二叉树的搜素之中。如果在平衡二叉树中插入或者删除一个节点使得高度之差大于1,就要进行节点之间的旋转,将二叉树重新维持在一
个平衡状态,这样把插入、查找、删除的时间复杂度最好情况和最坏情况都维持在O(logN),但是频繁的旋转会使插入和删除浪费掉O(logN)左右的
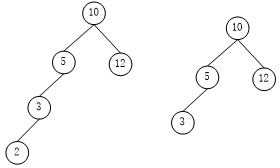
时间。如下图,两棵都是二叉查找树,但是只有右侧的是平衡二叉树。
平衡二叉树的实现大部分过程和二叉查找树是一样的,区别在于插入和删除之后需要写一个旋转算法来继续维持该树的平衡,维持平衡需要借助该节
点的高度属性来完成。
1.确定平衡二叉树的节点结构
平衡二叉树节点需要存放的值包含:节点的数值data、节点的高度height、节点的使用频率feq、指向节点的左
子树根节点的指针rchild,因此平衡二叉树的节点模板函数如下:
template<class T> class TNode{
public:
TNode():height(0),feq(1),lchild(NULL),rchild(NULL){}
T data;
int hgt,feq;
Tnode *lchild,*rchild;
};2.确定平衡二叉树的类声明
template<class T> class AVL-Tree
{
public:
void InsertPri(TNode<T>* node,T x); //插入
void DeletePri(TNode<T>* node,T x); //删除
void InSubTree(TNode<T>* node); //遍历
TNode<T>* FindPri(TNOde<T>* node,T x); //查找
int Height(TNode<T>* node);//求节点node的高度
//旋转:包含了四种情况:左左、右右、左右、右左
void SingRotateLeft(TNode<T>* &k2);
void SingRotateRight(TNode<T>* &k2);
void RotateLeftRight(TNode<T>* &k2);
void RotateRightLeft(TNode<T>* &k2);
int Max(int compa,int compb);
private:
PNode* root;//根节点
AVL-Tree():root(NULL){}
};3.旋转:对于一个平衡二叉树的节点来说,任意的节点顶多有2个子节点,因此不平衡时,此节点的两棵子树的高度差为2,因此插入一个新的节点有以下
四种情况:
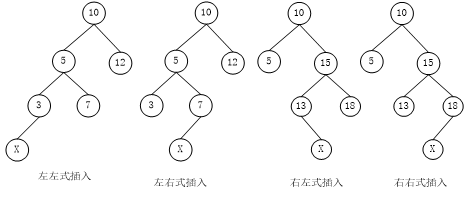
node的右孩子的左孩子处插入新的节点,简称右左式插入;(4)在节点node的右孩子的右孩子处插入新的节点,简称为右右是插入。各种插入方式如下
图所示:
由上图很容易看出来,情形1和4是对称的,情形2和3也是对称的。对于情形1和4中只需要经过一次选装就可以使新树达到平衡,我们称之为单选转;
对于情形2和3中需要进行两次选装才可以达到平衡,因此称之为双旋转。
3.1单旋转
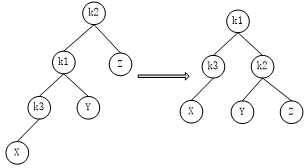
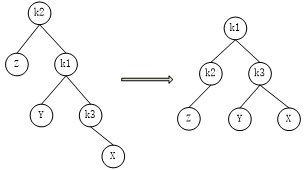
如下图,左左式插入
新树达到平衡时根节点k2经过了一次顺势针的旋转,根节点k2的左孩子节点k1成为了新的根节点,由于K2>k1,因此k2成为了
k1的右孩子节点,由于k1的右孩子大于k1小于k2(如果存在的话),因此k1的右孩子成为了k2的左孩子,若k1的右孩子为空,则以上操作为空操作,
不影响最终的结果。这样新加入节点后的二叉树又恢复成了平衡二叉树,同时k1的高度下降1,k2的高度上升1,则平衡二叉树的高度没有发生变化,
该过程称之为左左式旋转。
void RotateLeftLeft(TNode<T>* &k2)
{
Tnode<T>* k1;
k1=k2->lchid;
k1->rchild=k2;
k2->lchild=k1->rchild;
k2->hgt=Max(height(k2->lchild),height(k2->rchild))+1;
k1->hgt=Max(height(k1->lchild),k2->hgt)+1;//k2的hgt改变了
}如下图,右右式插入
右右式插入和左左式插入是对称的,因此方法和左左是类似,不再赘余,直接给出实现的代码。该过程称之为右右式旋转。
void RotateRightRight(TNode<T>* &k2)
{
Tnode<T>* k1;
k1=k2->rchid;
k1->lchild=k2;
k2->rchild=k1->lchild;
k2->hgt=Max(height(k2->lchild),height(k2->rchild))+1;
k1->hgt=Max(height(k1->rchild),k2->hgt)+1;//k2的hgt改变了
}3.2双旋转
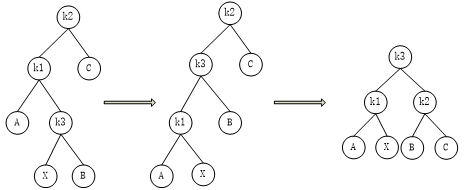
如下图,为左右式插入
对于左右式插入,单旋转是不能使它达到平衡状态的,需要经过两次旋转,第一次是节点k2的左孩子k1右右式旋转,第二次是节点k2左左式旋转。该
过程称之为左右是旋转,实现代码如下:
void RotateLeftRight(TNode<T>* &k2)
{
RotateRightRight(k2->lchild);
RotateLeftLeft(k2);
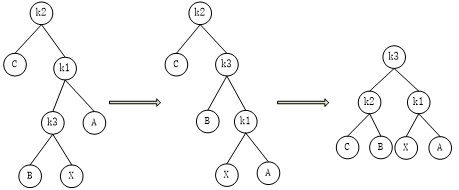
}如下图,为右左式插入
右右式插入和左右式插入是对称的,因此方法和左右是类似,不再赘余,直接给出实现的代码。该过程称之为右左式旋转。
void RotateLeftRight(TNode<T>* &k2)
{
RotateLeftLeft(k2->rchild);
RotateRightRight(k2);
}4.平衡二叉树的插入
平衡二叉树的插入和二叉查找树的插入方法是一样的,但是插入后需要从插入点开始维护到根节点的路径上的每一个节点的平衡性。可以根据插入的节点
的不同来选择不同的旋转算法实现树的平衡性。
template<class T>
void AVLTree<T>::InsertPri(TreeNode<T>* &node,T x)
//node为该树的根节点也就代表了这一棵树
{
if(node==NULL)//如果该树为空,则新建一个节点
{
node=new TNode<T>();
node->data=x;
return;
}
else if(node!=NULL)//该树不为空
{
if(node->data>x)//插入的数据小于根节点的值
{
InsertPri(node->lchikd,x);
//递归插入到根节点的左子树中,插入结束后判断该树是否为平衡树
//判断该节点是否平衡的方法是该节点左子树高度和右子树的高度差是否为2
if(2==height(node->lchild)-height(node->rchild))
{
//该节点值小于node->lchild->data,则插入为左左插入
if(x<node->lchild->data)
RotateLeftLeft(node);
else
RotateLeftRight(node);
}
}
else if(node->data<x)//插入的数据大于根节点的值
{
InsertPri(node->rchild,x);
if(2==height(node->rchild)-height(node->lchild))
{
if(x<node->rchild->data)
RotateRightLeft(node);
else
RotateRightRight(node);
}
}
else if(node->data==x)//插入的数据等于根节点的值
//不许要插入,只需要增加该节点的feq值
{
++node->feq;
}
node->hgt=Max(height(node->lchild),height(node->rchild));
}
}5.查找:和二叉树的查找相比,查找方法是不改变的,但是AVL-Tree可以将查找的时间维持在O(logn)时间内。
void FindPri(TNode<T>* node,T x)
{
if(node==NULL)
{
return NULL;
}
if(node->data>x)
{
FindPri(node->lchild,x);
}
if(node->data<x)
{
FindPri(node->rchild,x);
}
if(node->data==x)
{
return node;
}
}6.中序遍历:平衡二叉树的中序遍历和二叉树的中序遍历方法是一样的也是采用递归的方式。
void InSubTree(TNode<T>* node)
{
if(node==NULL) return ;
InSubTree(node->lchild);
cout<<node->data<<" ";
InSubTree(node->rchild);
}7.删除节点:如果删除的节点值小于根节点的值,递归在左子树中删除该节点;如果删除的节点值大于根节点的值,递归在右子树中删除该节点;如果删
除的节点值等于根节点的值,则删除该节点。删除元素结束以后需要判断该树是否为平衡二叉树,如果不为平衡二叉树需要做相应的旋转算法对该树进行
调整。
void DeletePri(TNode<T>* node,T x)
{
if(node==NULL) return ; //没有找到该平衡二叉树
if(x<node->data) //要删除的值小于node->data,则在node->lchild中递归实现删除x
{
DeletePri(node->lchild,x);
//删除x以后需要判断该二叉树是否保持平衡
if(2==height(node->rchild)-height(node->lchild)) //
{
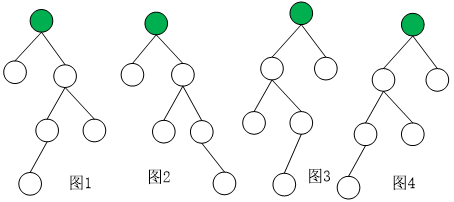
if(node->lchild->rchild!=NULL && height(node->lchild->rchild)>height(node->lchid->lchild))
//如下图1的情形,绿色节点表示要删除的节点
RotateLeftRight(node);
else //如下图2的情形,绿色节点表示要删除的节点
RotateLeftLeft(node);
}
}
else if(x>node->data)//要删除的值大于node->data,则在node->rchild中递归实现删除x
{
DeletePri(node->lchild,x);
//删除x以后需要判断该二叉树是否保持平衡
if(2==height(node->rchild)-height(node->lchild)) //
{
if(node->rchild->lchild!=NULL && height(node->rchild->lchild)>height(node->lchid->rchild))
如下图3的情形,绿色节点表示要删除的节点
RotateRightLeft(node);
else //如下图4的情形,绿色节点表示要删除的节点
RotateRightRight(node);
}
}
else if(x==node->data) //其他两种情况都是递归实现,但是这种情况就会复杂一些
{
//node左右孩子都存在,查找node左子树中data最大的节点作为新的node节点, 或者查找到node右子树中data最小的节点作为新的node节点
//我选择是的是找到node左子树中最大的作为新的node节点,另外一种方法是类推的
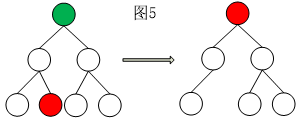
//如下图5的情形,绿色节点表示要删除的节点
if(node->lchild&&node->rchild) //node节点的左子树和右子树都存在
{
TNode<T>* temp=new TNode();
if(node->lchild!=NULL)
temp=node->lchild;
while(temp->rchild!=NULL)
{
temp=temp->rchild;
}
node->data=temp->data;
node->feq=temp->feq;
DeletePri(temp);
//删除结束后需要判断该树是否为平衡二叉树
if(2==height(node->rchild)-height(node->lchild))
{
if(node->rchild->lchild!=NULL && height(node->rchild->lchild)>height(node->rchild->lchild))
RotateRightLeft(node);
else
RotateRightRight(node);
}
}
else //node节点至多存在左子树或者右子树中的一个
{
TNode<T>* temp=node;
temp->data=node->data;
temp->feq=node->feq;
if(node->lchild==NULL)
node=node->rchild;
else if(node->rchild==NULL)
node=node->lchild;
delete(temp);
temp=NULL;
}
}
//更新node节点的高度hgt
node->hgt=Max(height(node->lchild),height(node->rchild));
return ;
}
8.Max()函数,求出左子树和右子树高度的最大值,最为树的高度
int Max(int hgta,int hgtb)
{
return hgta>hgtb?hgta:hgtb;
}本文是我自己学习了红黑树以后的一些见解,可能会有不对的地方,如果有请联系我,以便可以及时的更新,QQ179560574.






















 713
713











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








