A Survey of Quantization Methods for Efficient Neural Network Inference翻译

摘要

一旦将抽象的数学计算用于数字计算机上的计算，计算中就会出现数值的有效表示，操纵和通信的这些问题。与数值表示问题密切相关的是量化问题：以何种方式将一组连续的实数数字分布到一个固定离散的数字集合上，以最大程度地减少存储所需的位数，并最大程度地提高位参与计算准确性？ 每当存储和/或计算资源受到严重限制时，这种长期量化问题尤其重要，并且由于神经网络模型在计算机视觉，自然语言处理和相关领域的出色表现，近年来量化已成为最前沿的研究。从浮点数表示转变为低精度的固定整数值（4位或更少），具有将内存占用和延迟减少16倍的潜力；而且，实际上，在这些应用中，通常在实践中经常实现4倍至8倍的减少。因此，在实现与神经网络相关的高效计算时，量化最近被作为一个重要且非常活跃的研究毫不奇怪。在本文中，我们调查了量化深度神经网络计算中数值的问题，涵盖了当前方法的优点/缺点。通过这项调查及其组织，我们希望能够提出对当前的神经网络量化研究的有用快照，并给予一个智能组织化方式，以减轻对该领域未来研究的评估。

1.介绍

在过去十年中，我们观察到神经网络（NN）在各种类型问题上准确率显着提高，这通常是通过过度参数化的模型来实现。尽管这些过度参数化的NN模型的准确性已显着增加，但这些模型的巨大尺寸意味着无法在许多资源受限的应用中部署它们。这为普适深度学习的实现产生了一个问题，因为需要在资源受限的环境中以较低的能量消耗和高准确率来实时推理。普适深度学习被期望能够对广泛的应用产生重大影响，例如实时智能医疗监测，自动驾驶，音频分析和语音识别。
　　以最优准确率实现高效且实时的NN，需要重新考虑NN模型的设计，训练和部署。有大量文献通过使NN模型提高效率（在延迟，内存占用和能量消耗等方面）来解决这些问题，同时仍提供最优的准确率和泛化性的权衡。这些努力可以大致分类如下。
　　a）Designing efficient NN model architectures：这项工作的重点是根据其微观结构（例如，深度卷积的核类型或低秩分解）以及其宏观结构（例如，residual或inception等模块类型）来优化NN。这里的经典技术主要使用手动搜索找到了新的网络结构模块，这是不可扩展的。因此，一项新的工作是设计自动化机器学习（AutoML）和神经网络结构搜索（NAS）方法。在给定模型大小，深度和/或宽度约束的情况下，这些集束旨在以自动化的方式找到正确的NN结构。我们推荐有兴趣的读者阅读[54]，以获取NAS方法的最新调查。
　　b）Co-designing NN architecture and hardware together：最近的另一项工作是将NN网络结构调整（并共同设计）到特定目标硬件平台上。其重要性是因为NN组件的开销（就延迟和能量而言）是与特定硬件相关的。例如，具有专用高速缓存分层结构的硬件可以比没有这种缓存分层结构的硬件更有效地执行带宽界限。与NN架构设计类似，在结构-硬件共同设计的方法都是手动的，其中研究院将调整/更改NN结构，也可以使用自动化的AutoML和/或NAS技术
　　c）Pruning：减少NN的内存占用和计算成本的另一种方法是应用修剪。在修剪中，具有较低显著性（灵敏度）的神经元被删除，从而得到一个稀疏计算图。在这里，显著性较小的神经元是指那些移除后对模型输出/损失函数影响最小的神经元。修剪方法可以大致分为非结构化修剪和结构化修剪。对于非结构化修剪，无论神经元出现在任何地方，其显著性较小都将被移除。通过这种方法，可以进行破坏性的修剪，从而消除大多数NN参数，同时对模型的泛化性能的影响很小。但是，这种方法导致稀疏化矩阵操作，已知这很难被加速，通常是内存受限的。另一方面，对于结构化修剪，一组参数（例如，整个卷积滤波器）将被移除。这具有更改层和权重矩阵输入和输出形状的效果，因此仍然允许密集的矩阵操作。但是，破坏性的结构化修剪通常会导致明显的准确率下降。在保持最优性能的同时，使用高度修剪/稀疏化进行训练和推理仍然是一个开放性的问题。我们推荐有兴趣的读者阅读[66，96，134]，以对修剪/稀疏化的相关工作进行详尽的调查。
　　d）Knowledge distillation：模型蒸馏涉及训练一个大型模型，然后将其用作teacher来训练一个更紧凑的模型。模型蒸馏的关键思想是利用teahcer模型生成的“软”概率，这与使用硬分类标签不同，因为这些概率可以包含有关输入的更多信息。尽管在蒸馏方面进行了大量工作，但这里的主要挑战是仅使用蒸馏来达到较高的压缩比。与量化和修剪相比，在保持性能不变时，可以达到≥4倍的压缩，知识蒸馏方法往往具有可忽略的准确率下降，并具有破坏性压缩。但是，知识蒸馏与先前方法（即量化和修剪）的组合已显示出巨大的成功。
　　e）Quantization：最后，量化是一种在NN模型的训练和推理方面表现出巨大一致性的成功方法。尽管数值表示和量化的问题是与数字计算一样古老的问题，但神经网络提供了独特的改进机会。虽然本文关于量化的调查主要集中在推理上，但我们应该强调，量化的重要成功同样在NN训练中。特别是，半精度和混合精确训练的突破是主要驱动因素，使AI加速器中的吞吐量更高。但是，事实证明，如果没有进行大量调整，训练时很难低于半精度，而最近的大多数量化研究都集中在推理上。推理量化是本文的重点。
　　f）Quantization and Neuroscience：与NN量化略微相关（以及某些动机）是神经科学中的工作，这些工作表明人脑以离散/量化的形式将信息存储，而不是连续形式。这个想法的一个流行的理由是，以连续形式存储的信息将不可避免地被噪声损坏（噪声始终存在于物理环境中，包括我们的大脑，并且可以由热，感觉，外部，突触噪声等引起）。但是，离散的信号表示对于如此低级的噪声可能会更鲁棒。还提出了其他原因，包括离散表示的较高泛化能力及其在有限资源下的较高效率。我们将推荐读者阅读[228]，以彻底了解神经科学文献中的相关工作。
　　这项工作的目的是介绍量化中使用的当前方法和概念，并讨论此研究的当前挑战和机遇。为此，我们试图讨论最相关的工作。在调查的篇幅限制中，不可能讨论像NN量化一样大的领域中的每项工作；毫无疑问，我们会错过一些相关论文。我们对我们可能忽略的论文的读者和作者表示歉意。
　　对于本调查的结构，我们将首先在第二节中提供量化的简要历史，然后我们将在第三节中介绍量化的基本概念。这些基本概念与大多数量化算法共享，它们对于理解和部署现有方法是必要的。然后，我们在第四节中讨论更高级的主题。这些主要涉及最新的方法，尤其是对于低/混合精确量化的方法。然后，我们在第五节中讨论了硬件加速器中量化的含义，并特别关注边缘处理器。最后，我们在第七节中提供了一个摘要和结论。

2.GENERAL HISTORY OF QUANTIZATION

Gray和Neuhoff对截至1998年的量化史进行了非常好的调查[76]。这篇文章是一本很棒的工作，值得整体阅读。但是，为了方便读者，我们将简要总结文章中的一些关键点。量化是一种将较大（通常是连续的）集合中的输入值映射到较小（通常是有限的）集合中输出值的方法，具有较长的研究历史。舍入近似和截断是两种典型的例子。量化与微积分的基础有关，相关方法可以在1800年代初（以及更早的早期）看到，例如，在早期工作中至少需要大规模的（按照1800年代初的标准）数据分析。关于量化的早期工作可以追溯到1867年，其中，使用离散化来近似积分的计算；随后，在1897年，Shappard研究了舍入误差对整合结果的影响。最近，量化在数字信号处理中也很重要，因为用数字形式表示信号的过程设计涉及舍入近似，以及数值分析和数值算法的实现，其中在实数数字上的计算均在有限精度算术的情况下实现。
　　直到1948年数字计算机的出现，当时香农就撰写了有关数学信息论的开创性论文，量化的效果及其在编码理论中的效果得到了正式提出。特别地，香农在他的无损编码理论中指出，当编码事件具有不一致的概率时，使用相同数量的编码位是浪费的。他认为，一种更最佳的方法是根据事件的概率来改变位数，该概念现在称为variable-rate quantization。尤其是霍夫曼编码是由此激励的产生的。在1959年的随后工作中，香农引入了distortion-rate函数（在编码后为信号失真提供了更低的下限）以及矢量量化的概念（也在第四节的F子节中简要讨论）。这个概念已扩展并在[53, 55, 67, 208] 中进行实用，用于真实的通信应用。在该时间段内信号处理中量化的其他重要历史研究包括[188]，该研究引入了Pulse Code Modulation (PCM)概念（提出了近似/表示/编码采样的模拟信号的脉冲方法），以及经典的高分辨率量化。我们推荐有兴趣的读者阅读[76]，以详细讨论这些问题。
　　量化在算法中以略有不同的方式出现，这些算法使用数值近似来解决涉及连续数学量化的问题，该领域也有很长的历史，但随数字计算机的出现重新引起了人们的兴趣。在数值分析中，一个重要的概念是（现在仍然是）well-posed problem，即如果一个问题的解是存在的，解是唯一的，且解能根据初始条件连续变化，不会发生跳变，即解必须稳定。该问题有时称为well-conditioned problems。事实证明，即使处理一个条件良好的问题，一些在理想情况下能够完全解决该问题的算法，也会由于舍入和截断误差引入的噪声，表现的很糟糕。舍入误差与用量化指定的有限位数表示实数数字有关，例如IEEE浮点数标准；由于实际上只能执行迭代算法的有限数目迭代，因此出现截断误差。即使在“精确算术”中，后者也很重要，因为连续数学的大多数问题无法通过有限的基本操作序列来解决。但是前者与量化有关。这些问题导致了算法的numerical stability的概念。让我们将一个数值算法视为试图将输入数据$x$映射到真正解决方案$y$的函数$f$；但是由于舍入错误和截断错误，算法的输出实际上是$y^{\ast }$。在这种情况下，算法的正向误差为$∆y=y^{\ast }-y$；算法的后向误差是最小值$∆x$，以使$f(x+∆x)=y^{\ast }$。因此，正向误差告诉我们确切或真实答案与算法输出之间的区别。后向误差告诉我们我们实际运行的算法的输入数据是什么。算法的正向误差和后向误差与问题的条件数目相关。我们推荐有兴趣的读者阅读[237]，以详细讨论这些问题。

2.1 Quantization in Neural Nets

毫无疑问，数以千计的论文已经探索这个主题，人们可能会想知道：NN量化的最新工作与这些早期作品有何不同？当然，许多最近提出的“新算法”与过去文献中的工作具有紧密的联系（而在某些情况下是重新发现）。但是，NN为量化问题带来了独特的挑战和机遇。首先，神经网络的推理和训练在计算上都是密集型的。因此，数值的有效表示特别重要。其次，大多数当前的神经网模型被过度参数化，因此有足够的机会可以降低位精度而不会影响准确率。但是，一个非常重要的区别是，NN对破坏性的量化和极端离散化非常鲁棒。这里的新自由度与涉及的参数数量有关，即我们正在使用的过度参数化的模型。无论我们对前向误差还是后向误差等感兴趣， 这对我们是否解决了well-posed problems具有直接的影响。在推动量化最新发展的NN应用中，没有一个well-posed或well-conditioned的问题被解决。取而代之的是，人们对某种前向误差的度量标准（基于分类质量，困惑度等）感兴趣，但是由于过度参数化，有许多完全不同的模型可以完全或大致优化此度量标准。因此，在量化模型和原始非量化模型之间可能具有高误差/距离，同时仍然达到很好的泛化性能。在许多经典研究中，这种额外的自由度并不存在，这些研究主要集中在寻找不会改变太多信号的压缩方法，或者使用数值方法来控制“精确”与“离散”计算之间的差距。这一观察结果一直是研究NN量化新技术的主要驱动力。最后，神经网络模型的分层结构为探索提供了一个额外的维度。神经网络中的不同层对损失函数有不同的影响，这激发了混合精度的量化方法。

3.BASIC CONCEPTS OF QUANTIZATION

在本节中，我们首先在3.1节中简要介绍了常见符号和问题的定义，然后我们在3.2到3.6节中描述了基本的量化概念和方法。之后，我们在3.7节中讨论了不同微调的方法，然后在3.8节节中讨论了随机量化。

3.1 Problem Setup and Notations

假设NN具有具有$L$层可学习的参数，表示为 { W 1 , W 2 , . . . , W L } \{W_1,W_2,...,W_L\} {W1​,W2​,...,WL​}，使用$\theta$表示所有这些参数的组合。不失一般性，我们专注于有监督学习问题，其中NN的目标是优化下式的经验风险最小化函数：
$$\mathcal{L}(\theta )=\frac{1}{N}\sum _{i=1}^{N}l(x_i,y_i;\theta ),\text{\hspace{1em}(1)}$$
其中$(x,y)$是输入数据和相应的标签，$l(x,y,\theta )$是损失函数（例如，均方误差或交叉熵损损失），$N$是数据的总数。我们将第$i$层的输入隐藏激活表示为$h_i$，以及相应的输出隐藏激活为$a_i$。我们假设我们已经训练了模型参数$\theta$，并以浮点精度存储。在量化中，目标是将参数（$\theta$）以及中间激活映射（即$h_i$，$a_i$）的精度降低，同时对模型的通用能力/准确率的影响最小。为此，我们需要定义一个量化运算符，该运算符将浮点值映射到一个量化值，该量化值在下面几节描述。

3.2 Uniform Quantization

　　我们首先需要定义一个可以将NN权重和激活量化为有限数值集合的函数。如图1所示，此函数获取浮点上的实数，并且将它们映射到较低的精度范围。量化函数的一个流行选择如下：
$$Q(r)=Int(r/S)-Z,\text{\hspace{1em}(2)}$$
其中$Q$是量化运算符，$r$是一个实数输入（激活或权重），$S$是实数的缩放因子，$Z$是整数零点。此外， $Int$函数通过舍入操作（例如最近舍入和截断）将实数映射到整数值。本质上，此函数是从实数$r$到某些整数值的映射。这种量化方法也称为uniform quantization，因为最终的量化值（也称为量化水平）是均匀间隔分布的（图1，左）。同样还有nonuniform quantization方法，其量化值不一定是均匀间隔分布的（图1，右），这些方法将在3.6节中更详细地讨论。可以通过通常称为dequantization的操作将量化值$Q(r)$恢复到实际值$r$：
$$\tilde{s}=S(Q(r)+Z).\text{\hspace{1em}(3)}$$
注意由于舍入误差，恢复的实数$\tilde{r}$不会与$r$完全匹配。

3.3 Symmetric and Asymmetric Quantization

　　均匀量化的一个重要因子是等式2中的缩放因子$S$的选择。该缩放因子本质上将给定的实数$r$分为多个分区（如[113，133]中所述）：
$$S=\frac{\beta -\alpha }{2^b-1},\text{\hspace{1em}(4)}$$
其中$[\alpha ,\beta ]$表示裁剪范围，这是一个我们用于裁剪实数的边界范围，而$b$是量化的位宽度。因此，为了定义缩放因子，应首先确定裁剪范围$[\alpha ,\beta ]$。选择裁剪范围的过程通常称为calibration。一个直接的选择是将信号的最小/最大值用作裁剪范围，即$\alpha =r_{min}$和$\beta =r_{max}$。这种方法是一种asymmetric quantization方案，因为裁剪范围不一定相对于原点对称（即$-\alpha \ne \beta$），如图2（右）所示。 也可以通过选择一个对称的裁剪范围$\alpha =-\beta$来使用symmetric quantization方案。一个流行的方式是根据信号的最小/最大值进行选择：$-\alpha =\beta =max(|r_{max}|,|r_{min}|)$。与对称量化相比，不对称量化通常会导致更紧密的裁剪范围。当目标权重或激活不平衡时是非常重要的，例如，ReLU之后的激活始终具有非负值。但是，使用对称量化，通过用$Z=0$替换零点来简化等式2中的量化函数：
$$Q(r)=Int(\frac{r}{S}).\text{\hspace{1em}(5)}$$
　　在这里，缩放因子有两种选择。 在“全范围”对称量化中$S$被选择为$\frac{2max(|r|)}{2^n-1}$（具有向下舍入模式），以使用$[-128,127]$的完整$INT8$范围。但是，在“限制范围”中，$S$被选择为$\frac{max(|r|)}{2^{n-1}-1}$，仅使用$[-127,127]$的范围。如所期望的那样，全范围方法更准确。在实践中广泛采用对称量化以量化权重，因为省略零点可以使推理期间的计算成本降低，并且也使实现更加直接。但是，请注意对于激活则使用另一种量化，这是由于非对称激活中的偏移是一个静态数据独立项，并且可以在偏差中被吸收（或用于初始化累加器）。
　　使用信号的min/max，对于对称和不对称量化都是一种流行方法。但是，这种方法容易受到激活中的异常值的影响。这些异常值可能会增加范围，从而减少量化的分辨率。解决此问题的一种方法是使用百分位数而不是信号的min/max。也就是说，使用第$i$个最大或最小值作为$\beta /\alpha$。另一种方法是选择$\alpha$和$\beta$，以最小化实数和量化值之间的KL散度（即信息损失）。我们推荐感兴趣的读者阅读[255]，其在各种模型上评估了不同的校准方法。
　　Summary (Symmetric vs Asymmetric Quantization)。对称量化使用一个对称范围对分区进行裁剪。这具有更容易实现的优点，因为它导致等式2中的$Z=0$。但是，对于可能偏斜而不是对称范围的情况，它是次优的。对于这种情况，首选不对称量化。

3.4 Range Calibration Algorithms: Static vs Dynamic Quantization

到目前为止，我们讨论了用于确定裁剪范围$[\alpha ,\beta ]$的不同校准方法。量化方法的另一个重要区别是何时确定裁剪范围。该范围可以在静态权重下计算，因为在大多数情况下，参数在推理过程中是固定的。然而，每个输入样例的激活映射都不同（等式1中的$x$）。因此，有两种量化激活的方法：dynamic quantization和static quantization。
　　在动态量化中，该范围是在运行期间对每个激活映射动态计算的。这种方法需要对信号的统计数据（min, max, percentile等）进行实时计算，这可能具有很高的开销。但是，动态量化通常会导致更高的精度，因为对于每个输入都精确地计算了信号范围。
　　另一种量化方法是静态量化，其裁剪范围在推理过程中是预计算并固定的。这种方法不会添加任何计算开销，但与动态量化相比，它通常会导致较低的准确性。预计算的一种流行方法是运行一系列校准输入来计算典型的激活范围。已经提出了多种不同的度量指标来找到最优范围，包括最小化原始非量化权重分布与相应量化值之间的均方误差（MSE）。尽管MSE是使用最常见的方法，但也可以考虑使用其他度量指标，例如熵。 另一种方法是在NN训练期间学习/强加此裁剪范围。这里值得注意的工作是LQNets，PACT，LSQ和LSQ+，它们在训练过程中共同优化了NN的裁剪范围和权重。
　　Summary (Dynamic vs Static Quantization)。动态量化动态计算每种激活的裁剪范围，并且通常达到最高精度。但是，动态计算信号的范围非常昂贵，因此，实际场景最常使用静态量化，其中裁剪范围对于所有输入都是固定的。

3.5 Quantization Granularity

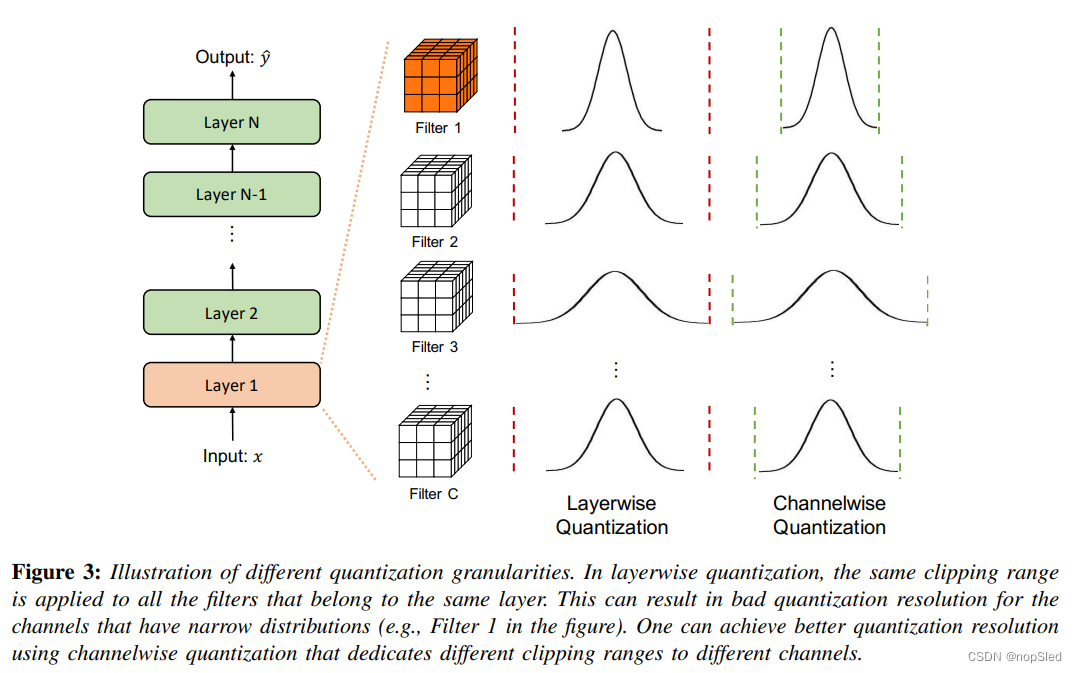
　　在大多数计算机视觉任务中，一个层使用多种不同的卷积滤波器进行卷积，如图3所示。这些卷积滤波器中的每一个都可以具有不同的值范围。因此，量化方法的一种区别是如何计算权重剪切范围$[\alpha ,\beta ]$的粒度。我们将它们分类如下。
　　a）Layerwise Quantization：在这种方法中，裁剪范围是通过考虑同一层中卷积滤波器中的所有权重来确定的，如图3的第三列所示。在这里，人们检查了该层中所有参数的统计数据（min, max, percentile等），然后在所有卷积滤波器中使用相同的裁剪范围。尽管这种方法非常易于实现，但通常会导致次优准确率，因为每个卷积滤波器的范围可能会有很大变化。例如，由于同一层中的另一个卷积核比另一个卷积核具有更宽的范围，因此具有相对较窄的参数范围的卷积核可能会使使量化分辨率降低。
　　b）Groupwise Quantization：可以在一层内部进行分组多个不同的通道，以计算（激活或卷积内核的）裁剪范围。这对于在单个卷积/激活中分布的参数分布差异很大时可能会有所帮助。例如，在Q-BERT中发现这种方法可用于量化由完全连接注意力层组成的Transformer模型。但是，这种方法不可避免地会带来有关不同缩放因子的额外计算。
　　c）Channelwise Quantization：裁剪范围的一个流行选择是为每个卷积滤波器（独立于其他通道）使用一个独立的固定值，如图3的最后一列所示，也就是说，每个通道都分配了一个专用的缩放系数。这样可以确保更好的量化分辨率，并且通常会导致更高的准确性。
　　d）Sub-channelwise Quantization：可以将上一个方法看作一种极端情况，在这种情况下，卷积或完全连接层中的任何参数组都独立确定裁剪范围。但是，这种方法可能会增加大量的开销，因为处理单个卷积核或完全连接层时需要考虑不同的缩放因子。因此，逐组量化可以在量化分辨率和开销之间建立良好的平衡。
　　Summary (Quantization Granularity)。Channelwise量化是当前用于量化卷积核的标准方法。它使研究员可以用可忽略的开销来调整每个卷积核的裁剪范围。相比之下，sub-channelwise量化可能会导致大量的开销，目前并不是标准选择（我们推荐有兴趣的读者阅读[68]，以了解与这些设计选择相关的权衡）。

3.6 Non-Uniform Quantization

文献中的某些工作还探索了非均匀量化，其中量化步骤以及量化水平被允许不均匀地间隔分布。等式6中显示了非均匀量化的形式定义，其中$X_i$代表离散量化水平，${∆}_i$表示量化步骤（阈值）：
$$Q(r)=X_i,ifr\in [{∆}_i,{∆}_{i+1})\text{\hspace{1em}(6)}$$
具体而言，当实数$r$的值处于量化步骤${∆}_i$和${∆}_{i+1}$之间时，量化$Q$将其映射到相应的量化水平$X_i$。请注意，$X_i$和${∆}_i$的分布都是不均匀的。
　　当bit宽度固定时，非均匀量化的量化可能会达到更高的精度，因为人们可以通过更多地关注重要的值区域或找到适当的动态范围来更好地捕获分布。例如，许多非均匀量化方法已设计用于通常涉及长尾的权重和激活的钟形分布。典型的基于规则的非均匀量化是使用对数分布，在该分布中，量化步骤和水平呈指数增长而不是线性增加。另一个受欢迎的分支是基于二进制码的量化，其中实数矢量$\text{r}\in {\mathbb{R}}^n$通过具有因子${\alpha }_i\in \mathbb{R}$和二进制矢量 b i ∈ { − 1 , + 1 } n \textbf b_i∈\{-1,+1\}^n bi​∈{−1,+1}n的表示$\text{r}\approx {\sum }_{i=1}^m{\alpha }_i{\text{b}}_i$，量化到$m$个二元向量。由于没有闭式解可以最小化$\text{r}$和${\sum }_{i=1}^m{\alpha }_i{\text{b}}_i$之间的误差，因此先前的研究依赖于启发式方法。为了进一步改善量化器，最新的工作将非均匀量化作为优化问题。如等式7所示，量化$Q$中的量化步骤/水平被调整，以最小化原始张量和量化张量之间的差异。
$$\underset{Q}{\min }||Q(r)-r|{|}^2\text{\hspace{1em}(7)}$$
　　此外，量化器本身也可以与模型参数共同训练。这些方法称为可学习的量化器，量化步骤/水平通常通过迭代优化或梯度下降进行训练。
　　除了基于规则和基于优化的非均匀量化外，聚类也可以用于减轻由于量化而导致的信息损失。一些工作在不同的张量上使用k-means来确定量化步骤和级别，而其他工作则在权重上应用了Hessian-weighted k-means聚类，以最小化性能损失。可以在第4.6节中找到进一步的讨论。
　　Summary (Uniform vs Non-uniform Quantization)。通常，非均匀的量化使我们能够通过不均匀的分配位以及离散参数范围，从而更好地捕获信号信息。但是，通常难以在通用计算硬件（例如GPU和CPU）上有效部署非均匀量化方案。因此，均匀量化是当前普遍使用的方法，因为它的简单性和对硬件高效映射。

3.7 Fine-tuning Methods

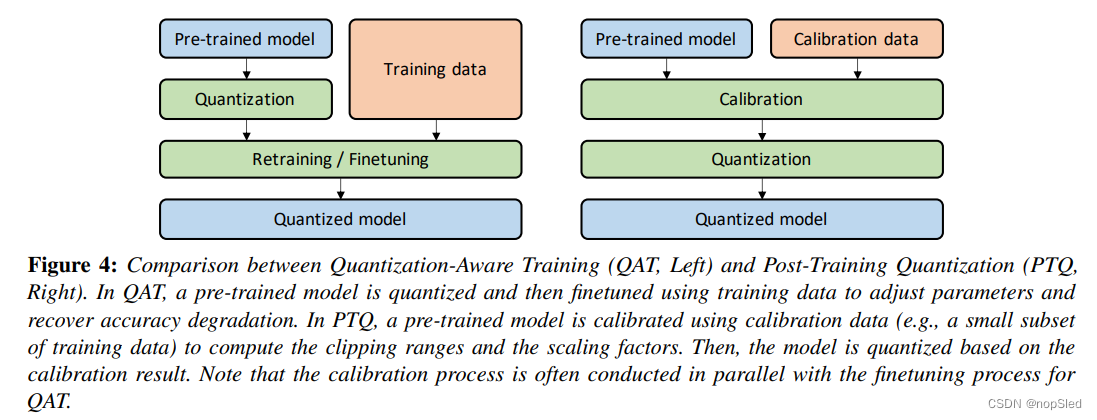
　　量化后通常需要调整NN中的参数。这可以通过重新训练模型来实现，该过程称为Quantization-Aware Training (QAT)，也可以在不重新训练的情况下完成，通常称为Post-Training Quantization (PTQ)。这两种方法之间的示意性比较如图4所示，并在下面进一步讨论（我们推荐有兴趣的读者阅读[183]，以进行有关此主题的更详细的讨论）。
　　1）Quantization-Aware Training：给定一个训练好的模型，量化可能会对训练的模型参数引入扰动，这可以将模型从用浮点精度进行训练时的收敛点上推离。可以通过用量化后的参数重新训练NN模型来解决此问题，以便模型可以收敛到更好的损失点。一种流行的方法是使用Quantization-Aware Training，其中通常以浮点精度对量化的模型执行向前和后向过程，然后在每个梯度更新后，对模型参数进行量化（类似于对梯度下降进行映射）。特别是，在以浮点精度执行权重更新后，进行此映射很重要。用浮点执行后向过程很重要，因为在量化精度下进行积累梯度可能会导致零梯度或者较高误差的梯度，尤其是在低精度中。
　　反向传播的重点是如何处理不可微分的量化运算符（等式2）。没有任何近似，该运算符的梯度几乎到处都是零，因为等式2中的舍入操作是piece-wise flat的操作。解决此问题的一种流行方法是通过Straight Through Estimator (STE)近似该操作符的梯度。STE基本上忽略了舍入操作，并用一致性函数将其近似，如图5所示。
　　尽管STE的近似很粗糙，但除了二进制量化之类的超低精度量外，它通常在实践中效果很好。[271]的工作为这种现象提供了理论上的支持，它发现STE的粗梯度近似可能与population梯度相关（适当选择STE）。从历史的角度来看，我们应该指出，STE的最初想法可以追溯到[209，210]的开创性工作，其中一个恒等操作符被用来近似二进制神经元的梯度。
　　尽管STE是主流方法，但在文献[2, 25, 31, 59, 144, 164]中也探讨了其他方法。我们应该首先提到[13]还提出了一种随机神经元方法作为STE的替代方法（在第3.8节中简要讨论了这一点）。另外还提出了使用组合优化，目标传播或Gumbel-softmax的其他方法。另一种不同类别的替代方法试图使用正则操作符来执行要量化的权重。这消除了在等式2中使用不可微分的量化运算符的需求。这些方法通常称为Non-STE方法。该领域的最新研究包括ProxQuant，其删除了量化等式2中的舍入操作，而使用所谓的W-shape，非平滑正则化函数来强制权重转换到量化值。其他值得注意的研究包括使用脉冲训练来近似不连续点的导数，或用浮点和量化参数的仿射组合代替量化的权重。[181]的最新工作也表明，AdaRound是一种自适应舍入方法，是round-to-nearest的替代方法。尽管在这一领域进行了有趣的工作，但这些方法通常需要大量的调整，到目前为止，STE方法是最常用的方法。
　　除了调整模型参数外，一些先前的工作还发现在QAT期间学习量化参数也有效。PACT在均匀量化下学习激活的裁剪范围，而QIT还学习了量化步骤和水平，以扩展到非均匀量化设置。LSQ引入了一种新的梯度估计值，以学习QAT期间非负激活（例如ReLU）的缩放因子，而LSQ+进一步将此思想扩展到了一般激活函数，例如能产生负激活的swish和h-swish。
　　Summary (QAT)。尽管STE的近似值很粗糙，但已证明在QAT可行。但是，QAT的主要缺点是重新训练NN模型的计算成本。可能需要进行数百个epoch的重新训练，以恢复准确率，尤其是对于低bit精度量化。如果打算将一个量化模型进行长期部署，并且效率和准确率尤为重要，那么对重新训练的投资可能值得。但是，情况并非总是如此，因为某些模型的寿命相对较短。我们接下来讨论一种没有这种开销的替代方法。
　　2）Post-Training Quantization：昂贵的QAT方法的替代方法是Post-Training Quantization (PTQ)，该方法在无需微调的情况下执行量化并调整权重。因此，PTQ的开销非常低，通常可以忽略不计。与需要足够数量的训练数据进行重新训练不同，PTQ具有额外优势，即可以在数据受到限制或未被标注的情况下应用。但是，与QAT相比，这通常是以较低的精度为代价的，尤其是对于低精度量化。
　　因此，已经提出了多种方法来减轻PTQ的准确率降低的问题。例如，[11,63]观察到量化后权重的均值和方差固有偏置，并提出偏置校正方法。[174,182]表明，平衡不同层或通道之间的权重范围（和隐式激活范围）可以减少量化误差。ACIQ通过分析计算PTQ的最佳裁剪范围和通道的位宽度设置。尽管ACIQ可以实现较低的精度降低，但是ACIQ中使用的逐通道激活量化很难在硬件上有效部署。为了解决这个问题，OMSE方法可以通过优化量化张量和相应的浮点张量之间的L2距离来移除激活上逐通道量化。此外，为了更好地减轻异常值对PTQ的不利影响，在[281]中提出了一种异常通道分割（OCS）方法，该方法将包含异常值的通道重复并减半。另一个值得注意的工作是AdaRound，它表明，用于量化的原始round-to-nearest方法本质上会得到一个次优解，并且提出了一种自适应舍入方法，可以更好地减少损失。尽管AdaRound将量化权重的变化限制为在其全精度的±1内，但AdaQuant提出了一种更通用的方法，该方法允许根据需要对权重进行量化。PT 方法的另一种极端情况是在量化过程中均未使用训练和测试数据（又称zero-shot场景），接下来将进行讨论。
　　Summary (PTQ)。在PTQ中，直接确定所有权重和激活的量化参数，而无需重新训练NN模型。因此，PTQ是量化NN模型的非常快速的方法。但是，与QAT相比，这通常是以较低的精度为代价。
　　3）Zero-shot Quantization：正如目前所讨论的，为了在量化后达到最低的准确率损失，我们需要访问整个训练数据的一部分。首先，我们需要知道激活的范围，以便我们能够裁剪值并确定适当的缩放因子（通常在文献中称为校准）。其次，量化模型通常需要微调来调整模型参数并恢复精度下降。但是，在许多情况下，在量化过程中无法访问原始训练数据。这是因为训练数据集要么太大而无法发布（例如 Google’s JFT-300M），或由于安全性或隐私问题而敏感（例如，医疗数据）。已经提出了几种不同的方法来应对这一挑战，我们将其称为zero-shot量化（ZSQ）。 受[182]的启发，我们首先描述了两个不同级别的zero-shot量化：

• Level 1：没有数据，也没有微调（ZSQ + PTQ）。
• Level 2：没有数据，但需要微调（ZSQ + QAT）。

Level 1允许更快，更轻松的量化而无需任何微调。微调一般比较耗时，并且通常需要额外的超参数搜索。但是，Level 2通常会导致更高的准确率，因为微调有助于量化模型避免准确率下降，尤其是在超低bit精度的设置中。[182]的工作使用了Level 1方法，该方法依赖于平衡权重范围和纠正偏置误差，以使给定的NN模型更适合量化，而无需任何数据或微调。但是，由于该方法基于（piece-wise）线性激活函数的尺度同变性属性，因此对于具有非线性激活的NN，例如具有GELU激活的BERT或具有Swish激活的MobileNetV3的NN是次优化的。
　　ZSQ研究的一个流行分支是生成与目标预训练模型的真实数据类似的合成数据。然后将合成数据用于校准和/或微调量化模型。该领域的早期工作利用生成对抗网络（GAN）来生成合成数据。通过使用预训练模型作为判别器，它可以训练生成器，以便其输出可以被判别器判断为好。然后，使用从生成器收集的合成数据样本，可以使用全精度的模型对量化模型进行知识蒸馏（有关更多详细信息，请参见4.4节）。但是，此方法无法捕获真实数据的内部统计信息（例如，中间层激活的分布），因为它仅使用模型的最终输出而生成。不考虑内部统计数据的合成数据可能无法正确表示真实的数据分布。为了解决这个问题，许多随后的努力使用存储在Batch Normalization (BatchNorm)中的统计数据，即通道的均值和方差，以生成更真实的合成数据。特别是，[85]通过直接最小化内部统计数据的KL散度来生成数据，并使用合成数据来校准和微调量化模型。此外，ZeroQ表明合成数据可用于敏感性测量和校准，从而实现混合精度PTQ，而无需访问训练/验证数据。ZeroQ还将ZSQ扩展到目标检测任务，因为它在生成数据时不依赖输出标签。[85]和[24]都将输入图像设置为可训练的参数，并直接对其进行反向传播，直到它们的内部统计信息与真实数据相似。更进一步，最近的研究发现训练和利用生成式模型可以更好地捕获真实数据分布并生成更现实的合成数据。
　　Summary (ZSQ)。Zero Shot（又名数据无关）量化执行完整量化，而无需访问训练/验证数据。这对于想要加速自定义工作部署的机器学习提供商（MLaaS）尤其重要，而无需访问其数据集。此外，这对于安全或隐私问题可能限制访问训练数据的情况也很重要。

3.8 Stochastic Quantization

在推理期间，量化方案通常是确定性的。但是，这并不是唯一的可能性，有些工作探索了QAT的随机量化。与确定性量化相比，一个更高水平的直觉是随机量化可以允许NN探索更多。一个受欢迎的支持论点是，较小的权重更新可能不会导致任何权重变化，因为舍入操作可能总是返回相同的权重。但是，实现随机舍入可能会为NN提供逃脱的机会，从而更新其参数。
　　更正式的是，随机量化对浮点数向上或向下映射，其概率与权重更新的幅度相关。例如，在[29，79]中，等式2中的Int运算符定义为：
$$Int(x)=\{\begin{array}{ll}\lfloor x\rfloor & withprobability\lceil x\rceil -x,\\ \lceil x\rceil & withprobabilityx-\lfloor x\rfloor .\end{array}\text{\hspace{1em}(8)}$$
　　然而，这种定义不能应用于二进制量化。因此[42]将其扩展为：
$$Binary(x)=\{\begin{array}{ll}-1& withprobability1-\sigma (x),\\ +1& withprobability\sigma (x),\end{array}\text{\hspace{1em}(9)}$$
其中，Binary是一个将实数$x$二值化的函数，$\sigma (\cdot )$是sigmoid函数。
　　最近，在QuantNoise中引入了另一种随机量化方法。QuantNoise在每个正向过程中量化了不同的随机权重子集，并用无偏梯度训练模型。在许多计算机视觉和自然语言处理模型中，这允许较低的精度量化，而不会导致明显的准确性下降。但是，随机量化方法的主要挑战是为每个权重更新创建随机数的开销，因此在实践中尚未被广泛采用。

4.ADVANCED CONCEPTS: QUANTIZATION BELOW 8 BITS

在本节中，我们将讨论量化的更高级主题，该主题主要用于低于INT8的量化。我们将在4.1节中首先讨论仅整数量化的模拟量化及其差异。之后，我们将在第4.2节讨论中混合精度量化的不同方法，然后在4.3节中进行基于硬件量化。然后，我们将在第4.4节中描述如何使用蒸馏来提高的量化精度，然后我们将在4.5节中讨论更低bit精度的量化。最后，我们将简在第4.6节中要描述矢量量化的不同方法。

4.1 Simulated and Integer-only Quantization

　　有两种常见的方法来部署量化的NN模型，simulated quantization（又称 fake quantization）和integer-only quantization（又称fixed-point quantization）。在模拟量化中，量化的模型参数以低精度存储，但是使用浮点算术进行操作（例如矩阵乘法和卷积）。因此，如图6（中间）所示，需要在浮点操作之前取消量化参数。因此，通过模拟量化，推理时无法完全受益于快速且高效的低精度逻辑。但是，在纯整数量化中，所有操作均使用低精度整数算术进行，如图6（右）所示。这允许通过高效的整数算术进行推理，而没有任何浮点的参数或激活。
　　通常，用浮点算术进行全精度推理可能有助于最终量化准确率，但这是以无法从低精度逻辑中受益为代价。在延迟，功耗和面积效率方面，低精度逻辑比全精度具有多种好处。如图7所示（左）所示，许多硬件处理器，包括NVIDIA V100和Titan RTX，都支持低精度算术的快速处理，这些处理可以增强推理吞吐量和延迟。此外，如图7（右）所示的45nm技术所示，低精度逻辑在能量和面积方面效率更高。例如，与FP32比，执行INT8的能源效率要额外高30倍，面积高116倍。
　　著名的纯整数量化工作包括[154]，其将Batch Normalization融合到先前的卷积层中，[113]提出了一种针对具有batch normalization的残差网络的纯整数计算方法。但是，这两种方法都限于ReLU激活。[132]的最新工作通过用整数算术近似GELU，Softmax和Layer Normalization来解决此限制，并进一步将纯整数量化扩展到Transformer结构。
　　Dyadic quantization是另一种纯整数量化的类别，其中所有缩放量都是用二进数进行执行的，它们是分子中具有整数值，分母中具有2的幂的有理数。这将产生一个计算图，该计算图仅需要整数加法，乘法，位移动，而没有整数除。重要的是，在这种方法中，所有加法（例如残差连接）都具有相同的二进制缩放，这可以使加法逻辑更简单，并具有更高的效率。
　　Summary (Simulated vs Integer-only Quantization)。通常，与模拟/假量化相比，传统纯整数量化和二进制量化更为理想。这是因为纯整数使用具有低精度逻辑的算术，而模拟量化使用浮点逻辑来执行操作。但是，这并不意味着假量化永远不会有用。实际上，假量化方法对于带宽限制而不是计算限制的问题是有用的，例如在推荐系统中。对于这些任务，瓶颈是内存占用和从内存中加载模型的成本。因此，对于这些情况，执行假量化是可以接受的。

4.2 Mixed-Precision Quantization

　　很容易看出，当我们使用低精度量化时，硬件性能会提高。但是，将模型均匀量化为超低精度会导致明显的准确率下降。这可以通过混合精度量化解决此问题。在这种方法中，每一层均以不同的bit精度进行量化，如图8所示。该方法的一个挑战是，选择bit设置的搜索空间与层的数目呈指数相关。目前已经提出了不同的方法来解决这个巨大的搜索空间。
　　为每一层选择此混合精度本质上是一个搜索问题，并且已经提出了许多不同的方法。[246]的最新工作提出了一种基于强化学习（RL）的方法来自动确定量化策略，作者使用一个硬件模拟器作为RL agent在硬件加速器中的反馈。[254]的论文将混合精度搜索问题作为神经网络结构搜索（NAS）问题提出，并使用可微分的NAS（DNAS）方法有效地探索了搜索空间。这些基于探索的方法的缺点是它们通常需要大量的计算资源，并且其性能通常对超参数甚至初始化敏感。
　　另一种混合精度方法使用周期函数正则化来训练混合精度模型，通过自动区分不同的层及其在精度方面的重要性，同时学习各自的位宽度。
　　与这些基于探索和正则化的方法不同，HAWQ引入了一种自动化方法，以基于模型的二阶灵敏度找到混合精度配置。从理论上讲，二阶操作符（即Hessian）的迹可用于测量层对量化的敏感度，类似于在Optimal Brain Damage这一开创性工作中裁剪的结果。在HAWQv2中，将此方法扩展到混合精度激活量化，并显示出比基于RL的混合精度方法快100倍以上。最近，在HAWQv3中，引入了一个纯整数，基于硬件的量化，该量化提出了一种快速整数线性编程方法，以针对给定应用找到符合特定约束（例如，模型大小或延迟）的最佳位精度。这项工作还通过直接在T4 GPU上部署模型解决了混合精度量化的硬件效率的常见问题，与INT8量化相比，使用混合精度（INT4/INT8）量化的速度高达50％。
　　Summary (Mixed-precision Quantization)。事实证明，混合精度量化是对不同NN模型低精度量化的有效且高效的方法。在这种方法中，NN的层被分组为是否对量化敏感/不敏感，并且每层都使用较高/较低的位。因此，可以最大程度地减少准确率下降，并且仍然受益于减少的内存占用和以低精度量化提高的速度。最近的工作还表明，这种方法是硬件高效的，因为混合精度仅在操作/层之间使用。

4.3 Hardware Aware Quantization

4.4 Distillation-Assisted Quantization

4.5 Extreme Quantization

4.6 Vector Quantization

5.QUANTIZATION AND HARDWARE PROCESSORS

6.FUTURE DIRECTIONS FOR RESEARCH IN QUANTIZATION