FlashAttention: Fast and Memory-Efficient Exact Attention with IO-Awarenes翻译

摘要

Transformers在长序列处理上是非常缓慢，且耗费内存的，因为自注意力的时间和空间复杂度为序列的二次方。近似注意力的方法试图通过平衡模型质量以降低计算复杂度来解决此问题，但通常无法实现wall-clock的加速。我们认为，失败的原则是缺少一个基于IO的注意力算法，以在GPU层级之间进行读写。我们提出了FlashAttention，这是一种基于IO精确注意力算法，该算法使用tiling(分块)技术来减少GPU高带宽内存（high bandwidth memory，HBM）和GPU的on-chip内存（SRAM）之间的内存读/写数量。我们分析了FlashAttention的IO复杂度，表明与标准注意力相比，它仅需更少的HBM访问量，并且对于各种SRAM尺寸而言都是最优的。我们还将FlashAttention扩展到block-sparse注意力，从而产生了比任何现有的近似注意力方法更快的注意力算法。使用FlashAttention训练Transformers比现有基准更快：与MLPerf 1.1训练速度记录相比，在BERT-large (seq. length 512)上达到15％的端到端wall-clock加速，在GPT-2 (seq. length 1K)上达到3倍加速，在long-range arena (seq. length 1K-4K) 上达到2.4倍加速。FlashAttention的block-sparse FlashAttention可以在Transformers中实现更长的上下文，从而产生更高质量的模型（在GPT-2上获得0.7的困惑收益，在长文档分类上获得6.4点的提升）和全新的功能：第一个在Path-X (seq. length 16K, 61.4% accuracy) 和 Path-256 (seq. length 64K, 63.1% accuracy) 上达到更好性能的Transformers。

1.介绍

　　Transformer模型已成为自然语言处理和图像分类等应用中最广泛使用的网络结构。Transformers逐渐变得更大和更深，但是使用更长的上下文仍然很困难，因为他们的核心，自注意力模块的时间和内存复杂度是序列长度的二次方。一个重要的问题是，提高注意力计算速度及内存效率是否可以帮助Transformer模型解决其运行时长和长序列的内存挑战。
　　许多近似注意力方法旨在减少注意力的计算和内存要求。这些方法的范围包括稀疏近似，低秩近似，以及他们的组合。尽管这些方法将计算需求降低到序列长度的线性或接近线性复杂度，但其中许多方法并未在标准注意力方面表现出wall-clock加速，也没有获得广泛的采用。一个主要原因是它们专注于减少FLOP（可能与wall-clock速度无关），并且倾向于忽略内存访问（IO）的开销。
　　在本文中，我们认为失败的原则是缺少一个基于IO的注意力算法。也就是说，需要仔细考虑不同级别的快慢内存的读写（例如，在较快的GPU on-chip内存SRAM和相对较慢的GPU高带宽内存HBM之间的读写，图1左）。在目前的GPU上，计算速度要快于存储速度，并且在Transformers中的大多数操作都被内存访问所限制。当数据的读写操作需要作为运行时长的一部分考虑时，基于IO的算法对于类似的内存受限的操作至关重要，例如数据库加入，图像处理，数值线性代数等。但是，通用的Python深度学习接口（例如Pytorch和Tensorflow）不允许对内存访问进行细粒度的控制。
　　我们提出了FlashAttention，这是一种新的注意力算法，该算法以更少的内存访问来实现计算精确（而不是近似）的注意力。我们的主要目标是避免对HBM进行注意力矩阵的读写。这需要：（i）计算softmax而无需访问整个输入（ii）不存储用于反向传播的大型中间注意力矩阵。我们采用两种完善的技术来应对这些挑战：（i）我们将注意力计算重构以将输入分为若干块，并在输入块上进行多次计算，从而增量执行softmax（也称为tiling）。（ii）我们存储了来自前向过程中的softmax归一化因子，以在反向过程中在SRAM上快速重新计算，这比读取HBM的中间注意矩阵的标准方法更快。我们在CUDA中实施FlashAttention，以实现对内存访问的细粒度控制，并将所有注意力操作融合到一个GPU核中。即使由于重新计算而引起的FLOPs增加，我们的算法都运行得更快（在GPT-2上达到7.6倍加速，图1右），并且使用比标准注意力更少的内存（与序列长度呈线性），这要归功于对HBM访问量的减少。
　　我们分析了FlashAttention的IO复杂度，与标准注意力的$\Omega (Nd+N^2)$相比，证明它需要$O(N^2{d}^2{M}^{-1})$的HBM访问，其中$d$是注意力头的维度，而$M$是SRAM的大小 。对于$d$和$M$的经典值，与标准注意力相比，FlashAttention的HBM访问次数更少（如图2所示，是标准的9倍）。此外，我们提供了一个下限，表明非精确注意力算法会逐渐提高HBM的访问次数。
　　我们还表明，FlashAttention可以通过克服内存访问开销来实现近似注意力算法。作为该概念的证明，我们实现了block-sparse FlashAttention，这是一种稀疏注意力算法，比FlashAttention快2-4倍，并将序列长度扩展为64K。我们证明，通过与稀疏性比成正比的因素， block-sparse FlashAttention具有比FlashAttention更好的IO复杂度。我们在第5节中讨论了对其他操作的进一步扩展（多GPU上的注意力，kernel regression，block-sparse 矩阵乘法）。我们开源的FlashAttention使其更容易在此原始版本上构建。
　　我们从经验上验证了FlashAttention会加快模型训练的速度，并通过建模更长的上下文来提高模型质量。与先前的注意力实现相比，我们还为FlashAttention和block-sparse FlashAttention的运行时长和内存占用构建了基准。

• Faster Model Training。FlashAttention以更快的wall-clock时间训练Transformer模型。我们训练的BERT-large (seq. length 512)比MLPerf 1.1中的训练速度记录快15％， GPT2 (seq. length 1K)比HuggingFace和Megatron-LM的基线块3倍，比long-range arena (seq. length 1K-4K) 的基线实现快3倍。
• Higher Quality Models。FlashAttention将Transformers扩展到更长的序列，从而提高了它们的质量并实现了新的功能。我们观察到GPT-2上的0.7困惑度的改进，以及长文档分类上建模更长序列带来6.4个点提升。FlashAttention启用了第一个可以在Path-X挑战上实现更好性能的Transformer，仅使用较长的序列长度（16K）。Block-sparse FlashAttention使Transformer可以扩展到更长的序列（64K），从而产生了第一个可以在Path-256挑战上实现更好性能的模型。
• Benchmarking Attention。FlashAttention的速度比传统128到2k的常见序列长度上的标准注意力快3倍，并能扩展到64K。对于512的序列长度，FlashAttention比任何现有的注意力方法都更快且内存更高效，而对于超过1K的序列长度，一些近似注意力方法（例如，Linformer）开始变得更快。另一方面，block-sparse FlashAttention的速度要比我们所知道的所有现有的近似注意力方法都快。

2.Background

我们提供了与深度学习操作相关的硬件（GPU）的性能特征的一些背景。我们还描述了注意力的标准实现。

2.1 Hardware Performance

我们在这里主要专注于GPU。其他硬件加速器上的性能可在[46，48]看到。
　　GPU Memory Hierarchy。GPU内存的层次结构（图1左）包括多种不同尺寸和速度，内存越小速度越快。例如，A100 GPU具有40-80GB的高带宽内存（HBM），其中带宽为1.5-2.0TB/s，每108个串流多处理器中的on-chip SRAM为192KB，带宽估计约为19TB/s。on-chip SRAM比HBM快很多数量级，但内存大小却要小很多。当计算速度比内存读取速度快时，对HBM内存的访问会变成操作的瓶颈。因此，利用更快的SRAM内存变得越来越重要。
　　Execution Model。GPU具有大量的线程来执行操作（称为GPU核）。每个核从HBM加载输入到寄存器，并且SRAM对其进行计算，然后将输出写入HBM。
　　Performance characteristics。基于计算和内存访问间的平衡，可以将操作分为计算受限或内存受限的。这通常是由arithmetic intensity来衡量的，其被定义为内存访问每个字节时算术操作的数量。

1. Compute-bound：操作所花费的时间取决于算术操作的数目，而访问HBM的时间则小得多。典型的示例是具有较大内积维度的矩阵乘法，以及大量通道的卷积。
2. Memory-bound：操作所花费的时间取决于内存访问的次数，而在计算中花费的时间要小得多。示例包括大多数其他操作：elementwise（例如activation，dropout）和reduction（例如，sum, softmax, batch norm, layer norm）。

Kernel fusion。加速memory-bound操作的最常见方法是kernel fusion：如果需要对同一输入应用多个操作，则可以从HBM加载一次输入，而不是为每个操作都加载一次。编译器可以自动融合许多elementwise操作。但是，在模型训练的背景下，中间值仍然需要写入HBM，以节省反向传播，从而降低了kernel fusion的有效性。

2.2 Standard Attention Implementation

　　给定输入序列$\text{Q},\text{K},\text{V}\in {\mathbb{R}}^{N\times d}$，其中$N$是序列长度，$d$是注意力头的维度，我们想去计算注意力输出$\text{O}\in {\mathbb{R}}^{N\times d}$：
$$\text{S}=\text{Q}{\text{K}}^T\in {\mathbb{R}}^{N\times N},\text{P}=softmax(\text{S})\in {\mathbb{R}}^{N\times N},\text{O}=\text{P}\text{V}\in {\mathbb{R}}^{N\times d},$$
其中softmax是逐行操作的。
　　标准注意力实现将矩阵$\text{S}$和$\text{P}$在HBM实现，其占用了$O(N^2)$的内存。通常$N\gg d$（例如，对于GPT2，$N=1024$和$d=64$）。我们在Algorithm 0中描述了标准注意力的实现。由于某些或大多数操作是内存受限的（例如softmax），因此大量的内存访问转化为较慢的wall-clock时间。
　　应用于注意矩阵的其他elementwise操作会加剧此问题，例如应用于$\text{S}$的屏蔽操作，或应用于$\text{P}$的dropout操作。结果，已经有许多尝试融合elementwise操作的尝试，例如屏蔽操作与softmax融合。
　　在第3.2节中，我们将证明标准注意力实现对HBM的访问是序列长度$N$的二次方。我们还比较了标准注意力和我们方法（FlashAttention）的FLOPs数量和HBM访问数量。

3.FlashAttention: Algorithm, Analysis, and Extensions

我们展示了如何使用更少的HBM读/写计算精确注意力，且无需为反向过程存储大型中间矩阵。这产生了一种注意力算法，在wall-clock时间内既有效又更快。我们分析了其IO复杂度，表明我们的方法与标准注意力相比只需要更少的HBM访问。我们进一步表明，通过将其扩展 到block-sparse attention，FlashAttention可以作为有用的原始操作。
　　我们将重点放在前向过程上，以便于说明；附录B包含后向过程的详细信息。

3.1 An Efficient Attention Algorithm With Tiling and Recomputation

　　给定HBM中的输入$\text{Q},\text{K},\text{V}\in {\mathbb{R}}^{N\times d}$，来计算注意力输出$\text{O}\in {\mathbb{R}}^{N\times d}$，并将其写入HBM。我们的目标是减少HBM访问的数量（长度$N$的sub-quadratic）。
　　我们应用两种已有的技术（tiling, recomputation）来克服以sub-quadratic HBM的访问计算精确注意力的技术挑战。我们在算法1中描述了这一点。主要思想是我们将输入$\text{Q},\text{K},\text{V}$分为块，并将它们从较慢的HBM中加载到较快的SRAM中，然后计算相对于这些块的注意力输出。通过到正确的归一化因子将每个块的输出缩放，并对这些块想加，我们将最终获得正确的结果。
　　Tiling。我们通过分块来计算注意力。Softmax连接$\text{K}$的列，因此我们用缩放解耦了大型softmax。对于数值稳定性，向量$x\in {\mathbb{R}}^{\text{B}}$的softmax被计算为：
$$m(x):=\underset{i}{\max }{x}_i,f(x):=[e^{x_1-m(x)}...e^{x_B-m(x)}],l(x):=\sum _{i}f(x{)}_i,softmax(x):=\frac{f(x)}{l(x)}.$$
　　对于向量$x^{(1)},x^{(2)}\in {\mathbb{R}}^{\text{B}}$，我们能够将两向量拼接$x=[x^{(1)}{x}^{(2)}]\in {\mathbb{R}}^{2\text{B}}$后的softmax解耦为：
$$m(x)=m([x^{(1)}{x}^{(2)}])=max(m(x^{(1)}),m(x^{(2)})),f(x)=[e^{m(x^{(1)})-m(x)}f(x^{(1)})e^{m(x^{(2)})-m(x)}f(x^{(2)})],$$
$$l(x)=l([x^{(1)}]x^{(2)})=e^{m(x^{(1)})-m(x)}l(x^{(1)})+e^{m(x^{(2)})-m(x)}l(x^{(2)}),softmax(x)=\frac{f(x)}{l(x)}.$$

因此，如果我们跟踪一些额外的统计数据（$m(x),l(x)$），则可以一次计算一个块的softmax。因此，我们将输入$\text{Q},\text{K},\text{V}$分块（算法1第3行），计算softmax的值以及额外的统计数据（算法1第10行），然后整合结果（算法1第12行）。
　　Recomputation。我们的目标之一是不存储用于反向传播的$O(N^2)$中间值。反向传播通常需要矩阵$\text{S},\text{P}\in {\mathbb{R}}^{N\times N}$来计算相对于$\text{Q},\text{K},\text{V}$的梯度。但是，通过存储输出$\text{O}$和softmax归一化统计量$(m,l)$，我们可以在反向传播过程中基于SRAM中的$\text{Q},\text{K},\text{V}$块重新计算注意力矩阵$\text{S}$和$\text{P}$。这可以看作是选择梯度检查点的一种形式。虽然研究建议梯度检查点要静尽可能减少所需的最大内存量，但我们知道的所有实现都平衡了内存和速度。相比之下，即使有更多的FLOPs，由于HBM访问的减少，我们的重新计算也会加快反向过程的速度（图2）。完整的反向过程说明可在附录B中查看。
　　Implementation details: Kernel fusion。tiling使我们能够在一个CUDA核中实现算法，首先从HBM加载输入，执行所有计算步骤（matrix multiply, softmax, optionally masking and dropout, matrix multiply），然后将结果写回HBM（masking和dropout可参看附录B）。 这避免了反复读写HBM的输入和输出。
　　Theorem 1。Algorithm 1返回$\text{O}=softmax(\text{Q}{\text{K}}^T)\text{V}$，其具有$O(N^{2}d)$的 FLOPs，并且需要除了输入和输出外还需要额外$O(N)$的内存。

3.2 Analysis: IO Complexity of FlashAttention

　　我们分析了 FlashAttentio的IO复杂度，与标准注意力相比，显示出HBM访问的显着降低。我们还提供了一个下界，证明没有精准注意力算法可以在所有SRAM尺寸上渐近地改善HBM访问次数。证明在附录C中。
　　Theorem 2。令$N$为序列长度，$d$为注意力头维度，并且$M$是SRAM的大小，其范围为$d\le M\le Nd$。标准注意力（Algorithm 0）需要$\Theta (Nd+d^2)$次HBM访问，而FlashAttention（Algorithm 1）则需要$\Theta (N^2{d}^2{M}^{-1})$次HBM访问。
　　对于$d$（64-128）和$M$（约100KB）的典型值，$d^2$要比$M$小很多倍，因此FlashAttention所需的HBM访问量要比标准注意力实现少很多倍。这既导致更快的执行和较低的内存占用，我们在第4.3节中验证了这一点。
　　证明的主要思想是，给定SRAM大小$M$，我们可以每次加载大小为$\Theta (M)$的$\text{K},\text{V}$块（算法1第6行）。对于$\text{K}$和$\text{V}$的每个块，我们在$\text{Q}$的所有块上迭代以计算中间值（算法1第8行），从而需要$\Theta (Nd{M}^{-1})$次的$\text{Q}$循环。而每一次循环需要加载$\Theta (Nd)$个元素，这就相当于$\Theta (N^2{d}^2{M}^{-}1)$次HBM访问。同样，我们证明标准注意力的反向过程需要$\Theta (Nd+N^2)$次HBM访问，而FlashAttention的反向过程需要$\Theta (N^2{d}^2{M}^{-}1)$次HBM访问（附录B）。
　　我们证明一个下界：证明没有精准注意力算法可以在所有SRAM尺寸上渐近地改善HBM访问次数。
　　Proposition 3。令$N$为序列长度，$d$为注意力头维度，并且$M$是SRAM的大小，其范围为$d\le M\le Nd$。对于所有范围$[d,Nd]$内的$M$，不存在算法在$o(N^2{d}^2{M}^{-1})$次HBM访问内来计算精确的注意力。
　　该证明依赖于以下事实：对于$M=\Theta (Dd)$，任何算法必须执行$\Omega (N^2{d}^2{M}^{-1})=\Omega (Nd)$次HBM访问。在串流算法文献中，这种类型的下界在$M$子范围上是常见的。我们将证明参数化的复杂度作为未来的工作。
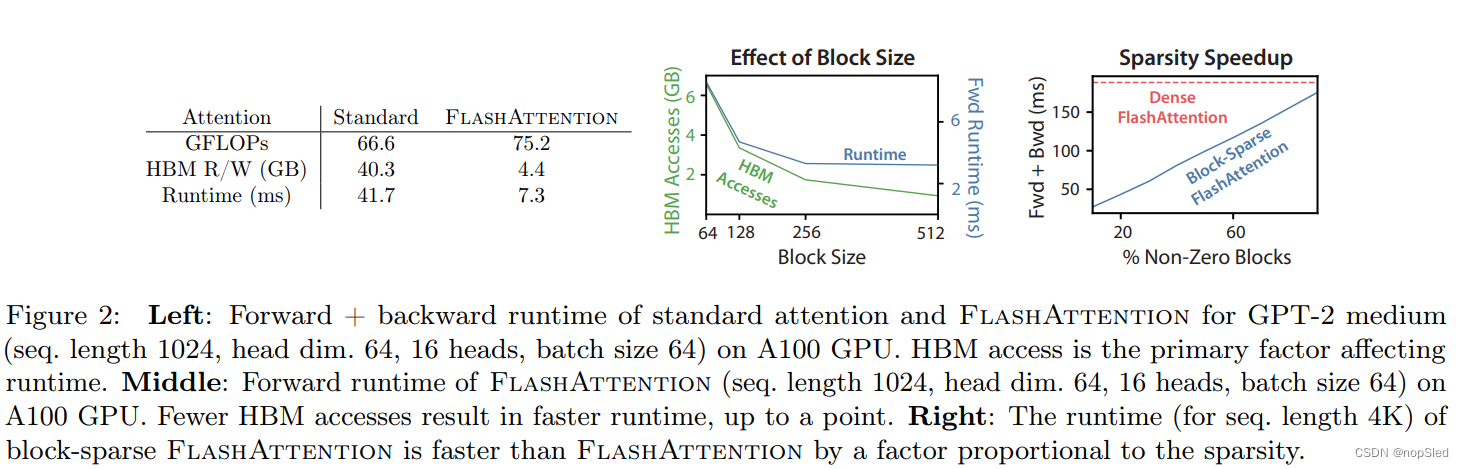
　　我们验证了HBM的访问次数是注意力运行时长的主要决定因素。在Fig. 2 (left)中，我们看到，即使与标准注意力相比，FlashAttention具有更高的FLOP（由于反向过程的重计算），它的HBM访问量也少得多，导致运行时间更快。在Fig. 2 (middle)中，我们改变了FlashAttention的块大小${\text{B}}_c$，这会导致不同的HBM访问量，并测量了前向过程的运行时长。随着块大小的增加，HBM访问的数量减少，运行时长也减少。对于足够大的块大小（超过256），则由其他因素（例如算术操作）变成了运行时长的瓶颈。此外，较大的块大小不会适合小型SRAM。

3.3 Extension: Block-Sparse FlashAttention

我们将FlashAttention扩展到近似注意力：我们提出了 block-sparse FlashAttention，其IO复杂度比FlashAttention小很多，并与稀疏性成正比。
　　给定一个输入$\text{Q},\text{K},\text{V}\in {\mathbb{R}}^{N\times d}$，以及一个mask矩阵 M ∈ { 0 , 1 } N × N \textbf M\in \{0,1\}^{N\times N} M∈{0,1}N×N，我们需要计算：
$$\text{S}=\text{Q}{\text{K}}^T\in {\mathbb{R}}^{N\times N},\text{P}=softmax(\text{S}\odot 1_{\tilde{M}})\in {\mathbb{R}}^{N\times N},\text{O}=\text{P}\text{V}\in {\mathbb{R}}^{N\times d},$$
其中$(\text{S}\odot 1_{\tilde{M}}{)}_{kl}={\text{S}}_{kl}if{\tilde{\text{M}}}_{kl}=1and-\infty if{\tilde{\text{M}}}_{kl}=0$。我们需要$\tilde{\text{M}}$具有一个块形式的mask矩阵：对于块大小${\text{B}}_r,{\text{B}}_c$，对于所有的$k,l$，${\tilde{\text{M}}}_{k,l}={\text{M}}_{ij}$，其中 M ∈ { 0 , 1 } N / B r , N / B c \textbf M\in \{0,1\}^{N/\textbf B_r,N/\textbf B_c} M∈{0,1}N/Br​,N/Bc​，且$i=\lfloor k/{\text{B}}_r\rfloor ,h=\lfloor l/{\text{B}}_c\rfloor$。
　　给定一个预定义的块稀疏mask矩阵 M ∈ { 0 , 1 } N / B r , N / B c \textbf M\in \{0,1\}^{N/\textbf B_r,N/\textbf B_c} M∈{0,1}N/Br​,N/Bc​，我们可以轻松地调整Algorithm 1仅计算注意力矩阵中的非零块。除了我们跳过mask为零的块外，该算法与Algorithm 1相同。我们在附录B中重现了Algorithm 5中的算法描述。
　　我们同样分析了block-sparse FlashAttention的IO复杂度。
　　Proposition 4。令$N$为序列长度，$d$为注意力头维度，并且$M$是SRAM的大小，其范围为$d\le M\le Nd$。Block-sparse FlashAttention (Algorithm 5) 需要$\Theta (Nd+N^2{d}^2/M^{-1}s)$次HBM访问，其中$s$是block-sparsity mask矩阵中非零块的分数。
　　我们看到，应用block-sparsity可以通过稀疏性直接改善IO复杂度。对于较大的序列长度$N$，通常将$s$设置为$N^{-1/2}$或$N^{-1}logN$，从而导致$\Theta (N\sqrt{N})$或$\Theta (NlogN)$的IO复杂度。对于下游实验，我们使用固定的butterfly sparsity
pattern ，该模式已被证明能够近似任意稀疏性。
　　在Fig. 2 (right)中，我们验证了随着稀疏性的增加，block-sparse FlashAttention的运行时长会按比例改善。在LRA基准测试上，block-sparse FlashAttention达到2.8倍的加速，同时性能以标准注意力相当（第4节）。

4.Experiments

A.Related Work

IO-Aware Runtime Optimization。在计算机科学中，优化快速/慢速内存中的读写具有悠久的历史，并且有许多知名的工作。在这篇工作中，我们直接将与分析I/O复杂性的文献联系在一起，但是内存分层结构的概念是基本的，并且以多种形式出现，包括工作集合模型，数据局部性，算术强度的Roof-line模型，可扩展性分析以及标准的计算机架构的教材。我们希望这项工作鼓励社区在深度学习堆栈中的更多部分中采用这些想法。
　　Efficient ML Models with Structured Matrices。矩阵乘法是大多数机器学习模型的核心计算瓶颈。为了降低计算复杂性，已经有许多方法可以学习一组更有效的矩阵。这些矩阵称为structured matrices，该矩阵具有参数量和运行时长的次二次方（对于$n\times n$维度，有$o(n^2)$）。结构化矩阵的最常见示例是稀疏和低秩矩阵，以及信号处理中通常遇到的快速变换（Fourier, Chebyshev, sine/cosine, orthogonal polynomials）。机器学习中提出了几类结构化矩阵：Toeplitz-like[78]， low-displacement rank[49]，quasi-separable[25]。受butterfly矩阵以及他们的积能表达任意结构化矩阵且具有最优运行时长和参数数目的驱动，我们在block-sparse attention中使用butterfly模式。但是，即使结构化矩阵在理论上是高效的，但它们并没有得到广泛的采用，因为很难将其效率转化为wall-clock加速，且密集无约束的矩阵乘具有非常优化的实现，这种现象称为hardware lottery [41] 。butterfly matrices的扩展[17，18]旨在使其更适合硬件。
　　Sparse Training。我们的block-sparse FlashAttention可以看作是能够使稀疏模型训练更高效的一步。由于通过稀疏化权重矩阵来进行推理，稀疏模型在压缩模型方面是成功的。对于模型培训，lottery tickets hypothesis表明，从一个较大的密集网络中得出的一组小型子网络，可以和原始密集网络性能相当。在注意力背景中，block-sparse FlashAttention也可以看作是一个固定的lottery tickets：通过训练，我们将稀疏模式固定为butterfly模式，并观察到在Long-range Arena任务上它的性能几乎和（密集）FlashAttention相当。
　　Efficient Transformer。基于Transformer的模型已成为自然语言处理和计算机视觉中最广泛使用的架构。但是，他们的计算瓶颈之一是它们的时间和内存大小是序列长度的二次方。有许多可以克服这种瓶颈的方法，包括使用哈希的近似，例如Reformer和Smyrf，以及低秩近似，例如Performer。甚至可以将稀疏和低秩近似结合起来，以提高准确性（例如，Longformer，BigBird，Scatterbrain，Long-short transformer ，Combiner）。其他方法包括对序列维度进行压缩，以一次计算一个或多个token。其中一种可以从以前的序列上访问状态，以帮助延长上下文（例如，Transformer-XL和Compressive Transformer）。 我们建议查看综述[81]以了解更多详细信息。
　　有一些其他工作研究开发其他模块而不是注意力模型以支持更长的上下文。HiPPO及其扩展，最著名的是S4，其以多项式偏差映射历史，从而可以通过状态空间模型准确地重建历史记录。它们结合了CNN（有效训练），RNN（有效推理）和连续模型（对采样率变化的鲁棒）的优势。LambdaNetworks[2]，AFT和FLASH是在图像分类和语言建模的背景下取代注意力的其他尝试。

B.Algorithm Details

B.1 Memory-efficient forward pass

B.2 Memory-efficient backward pass

B.3 FlashAttention: Forward Pass

B.4 FlashAttention: Backward Pass

C