进阶图论算法汇总（LCA、强（双）连通分量、欧拉路径与欧拉回路、拓扑排序、01规划）-acwing算法提高课 acm

LCA

向上标记法

时间复杂度 $O(n\ast m)$

如果两个结点不相同，就将较深的结点向上移动，直到移动到相同结点，那么该结点即为公共祖先结点。

代码

//预处理每个结点的深度，以及结点的父结点的编号
void dfs(int u, int father){
    depth[u]=depth[father]+1;
    fa[u]=father;

    for(int i=h[u];~i;i=ne[i]){
        int v=e[i];
        if(v!=father) dfs(v,u);
    }
}
//求u和v的公共祖先
int getlca(int u,int v){
    //只要u和v不同
    while(u!=v){
        //将深度大的结点向上移动
        if(depth[u]<depth[v]) v=fa[v];
        else u=fa[u];
    }
    return u;
}

倍增法

预处理 $O(nlogn)$

• $fa[i][j]$ 表示从节点$i$开始，向上走$2^j$步所走到节点的编号。若已经超出根节点,$fa[i][k]=0$。特别地,$fa[i][0]$就是$i$的根节点。

• $depth[i]$ 表示深度,根节点的深度为1,即$depth[root]=1$。

• 哨兵:如果从$i$开始跳$2^j$步会跳过根节点,那么$fa[i][j]=0$.$depth[0]=0$

• 递推关系：$fa[i][k]=fa[fa[i][k-1]][k-1]$

询问 $O(logn)$

1. 先将两个点跳到同一层
2. 让两个点同时向上跳，直到他们最近公共祖先的下一层

代码

int ne[maxn],e[maxn],h[maxn],idx;
int fa[maxn][21],dep[maxn];
int root;
void bfs(){
    queue<int>q;
    q.push(root);
    dep[root]=1,dep[0]=0;
    // 哨兵depth[0] = 0: 如果从i开始跳2^j步会跳过根节点 
    // fa[fa[j][k-1]][k-1] = 0
    // 那么fa[i][j] = 0 dep[fa[i][j]] = dep[0] = 0
    while(q.size()){
        int t=q.front(); q.pop();
        for(int i=h[t];~i;i=ne[i]){
            int j=e[i];
            if(dep[j]) continue;
            dep[j]=dep[t]+1;
            q.push(j);
            fa[j][0]=t;
            for(int k=1;k<=18;k++){ //注意边界
                fa[j][k]=fa[fa[j][k-1]][k-1];
            }
             /*
            举个例子理解超过根节点是怎么超过的
            因为我们没有对根节点fa[1][0]赋值,那么fa[1][0] = 0;
                 1
                / \
               2   3 
            fa[1][0] = 0;
            fa[2][0] = 1;
            fa[2][1] = fa[fa[2][0]][0] = fa[1][0] = 0;
            */
        }
    }
}

int lca(int x,int y){
    if(dep[x]<dep[y]) swap(x,y);
    for(int k=18;k>=0;k--)
        if(dep[fa[x][k]]>=dep[y])
            x=fa[x][k];
    
    if(x==y) return x;
    for(int k=18;k>=0;k--){
        if(fa[x][k]!=fa[y][k]){
            x=fa[x][k];
            y=fa[y][k];
        }
    }

    return fa[x][0];
}

Tarjan

时间复杂度 $O(n+m)$，离线做法

思路

在深度优先遍历时，将节点分为三大类：

1. 正在搜索的分支
2. 已经遍历过,且回溯过
3. 还未搜索到的点

我们画一个图可以发现第一类点都像一颗颗果实挂在某个点上当我们枚举到一个点的时候另一个点是第1类点那么他们的最近公共祖先就是第1类点挂着的点

所以我们可以去搜索如果在搜索过程中标记点是第几类点回溯的时候枚举有关这个点的询问如果另一个点是第1类点我们就可以得到这组询问的最近公共祖先

如果另一个点不是第一类点就暂时不管因为我们这个点很快就会变成第1类点到时候再拿那个点来完成这组询问的计算，最后我们再把当前点并入父节点，然后当前点变成二类点，最后再统一输出一下就可以完成离线解最近公共祖先

代码

/*
在深度优先遍历时,将所有点分成三大类:
[0] 还未搜索到的点
[1] 正在搜索的分支
[2] 已经遍历过,且回溯过
*/
void tarjan(int u){
    st[u]=1;
    // u这条路上的根节点的左下的点用并查集合并到根节点
    for(int i=h[u];~i;i=ne[i]){
        int j=e[i];
        if(st[j]) continue;
        tarjan(j);
        p[j]=u; //从左下回溯后把左下的点合并到根节点
    }

    // 对于当前点u 搜索所有的询问，查看是否可以得出结果
    for(auto item:ask[u]){
        int y=item.first,id=item.second;
        if(st[y]==2){ //该点已被回溯，也就是经过了并查集的合并
            int anc=find(y);
            ans[id]=dis[u]+dis[y]-dis[anc]*2; //保持原本次序输出
        }
    }
    st[u]=2; //点u已经搜索完且要回溯了 就把st[u]标记为2 
}

有向图的强连通分量 SCC

强连通图：给定一张有向图。若对于图中任意两个结点x，y，既存在从x到y的路径，也存在从y到x的路径，则称该有向图是“强连通图”。

强连通分量(SCC)指的是强连通图的极大连通子图（点最多的）。

说人话，强连通分量中任意两点都存在边，再加入任何别的点，它都不再是连通分量。

或者说，对于一张有向图，强连通分量就是任意两点都有路径(x能到y, y也能到x)，并且包含点最多的图。

有向图的强连通分量有什么用呢？

主要是通过缩点（将强连通分量缩成一个点），把有向图，转换为有向无环图（拓扑图，DAG）。

Tarjan

用途

• 有向图的缩点(有向图->有向无环图)

算法思路

1. 加时间戳，初始化i，j标志；
2. 放入栈中，做好标记；
3. 遍历邻点
   1. 如果没遍历过，tarjan一遍，用low[j]更新最小值low
   2. 如果在栈中，用dfn[j]更新最小值low
4. 找到最高点
   1. scc个数++
   2. do-while循环：
      从栈中取出每个元素；标志为出栈；
      对元素做好属于哪个scc；该scc中点的数量++

模板

// tarjan 算法求强连通分量
// 时间复杂度O(n+ m)
void tarjan(int u){
    // 初始化自己的时间戳
    dfn[u] = low[u] = ++ timestamp;
    //将该点放入栈中
    stk[++ top] = u, in_stk[u] = true;
    // 遍历和u连通的点
    for(int i = h[u]; ~i; i = ne[i]){
        int j = e[i];
        if(!dfn[j]){//如果没有遍历过，此时low[j]一定有值
            tarjan(j);
            // 更新u所能遍历到的时间戳的最小值
            low[u] = min(low[u], low[j]);
        }
        // 如果当前点在栈中
        // 注意栈中存的可能是树中几个不同分支的点,因为有横叉边存在
        // 栈中存的所有点，是还没搜完的点，同时都不是强连通分量的最高点
        // 这里表示当前强连通分量还没有遍历完，即栈中有值
        else if(in_stk[j])
            //更新一下u点所能到的最小的时间戳
            //此时j要么是u的祖先，要么是横叉边的点，时间戳小于u
            low[u] = min(low[u], dfn[j]);
    }
    // 找到该连通分量的最高点
    if(dfn[u] == low[u]){
        int y;
        ++ scc_cnt; // 强连通分量的个数++
        do{// 取出来该连通分量的所有点
            y = stk[top --];
            in_stk[y] = false;
            id[y] = scc_cnt; // 标记点属于哪个连通分量
            size_scc[scc_cnt] ++;
        } while(y != u);
    }
}

例题

AcWing 1174. 受欢迎的牛

#include<bits/stdc++.h>
using namespace std;

const int N = 10010, M = 50010;

int n, m;
int h[N], w[M], e[M], ne[M], idx; // 邻接表一套
// dfn[u] 存的是遍历到u的时间戳
// low[u]存的是从u出发，遍历子树，所能遍历到的最小的时间戳
//timestamp 就是时间戳
int dfn[N], low[N], timestamp;
int stk[N], top; // 栈，和栈顶元素索引
bool in_stk[N]; // 是否在栈中
//id[u]表示u的强连通分量的编号，scc_cnt表示强连通分量的编号
// size_scc[u]表示编号为u强连通分量中点的数量
int id[N], scc_cnt, size_scc[N];
int dout[N];// 记录新图中每个点（也就是原图每个连通分量）的出度

void add(int a, int b){
    e[idx] = b, ne[idx] = h[a], h[a] = idx ++;
}

void tarjan(int u){
    //当前点的时间戳
    dfn[u] = low[u] = ++ timestamp;
    // 加入栈中
    stk[++ top] = u, in_stk[u] = true;
    
    //遍历u点的所有邻点
    for(int i = h[u]; ~i; i = ne[i]){
        int j = e[i];
        if(!dfn[j]){//如果没有遍历过
            tarjan(j); // 遍历它
            low[u] = min(low[u], low[j]);
        }
        // 当前点在栈当中
        else if(in_stk[j]) low[u] = min(low[u], dfn[j]);
    }
    
    if(dfn[u] == low[u]){
        ++ scc_cnt; // 更新强连通分量的编号
        int y;
        do{
            y = stk[ top--]; //不断取出栈内元素
            in_stk[y] = false;
            id[y] = scc_cnt; //y元素所属的连通块编号
            size_scc[scc_cnt] ++; //该连通块内包含的点数
        }while(y != u); // 直到y不等于u
    }
    
}

int main(){
    cin >> n >> m;
    memset(h, -1, sizeof h);
    while(m --){
        int a, b;
        cin >> a >> b;
        add(a, b);
    }
    
    for(int i = 1; i <= n; i ++){
        if(!dfn[i])
            tarjan(i);
    }
    
    // 建有向无环图
    // 统计在新图中所有点的出度
    for(int i = 1; i <= n; i ++){
        for(int j = h[i]; ~j; j = ne[j]){
            int k = e[j];
            int a = id[i]; //a表示i所在连通分量的编号
            int b = id[k]; // b表示k所在连通分量的编号
            //如果点i和点k不在同一个连通块
            // dout存的是出度，因为本题只需要出度
            //在其他题目中，可能是要建边，因为这里是构造有向无环图
            if(a != b) dout[a] ++; // 从a走到b，a的出度++
        }
    }
    
    // 和本题有关的部分：
    // zeros是统计在新图中，出度为0的点的个数
    // sum表示满足条件的点（最受欢迎的奶牛）的个数
    int zeros = 0, sum = 0;
    for(int i = 1; i <= scc_cnt; i ++){
        if(!dout[i]){
            zeros ++;
            sum += size_scc[i];
            if(zeros > 1){
                sum = 0;
                break;
            }
        }
    }
    cout << sum << endl;
}

一些结论

• 缩点后，有$i$个起点、$j$个终点，再添加$max(i,j)$个边，可使其变成强连通。

无向图的双联通分量 DCC

分类

• 边双联通分量 e-DCC
  • 极大的不包含桥的连通块
• 点双联通分量 v-DCC
  • 极大的不包含割点的连通块

缩点后变成树

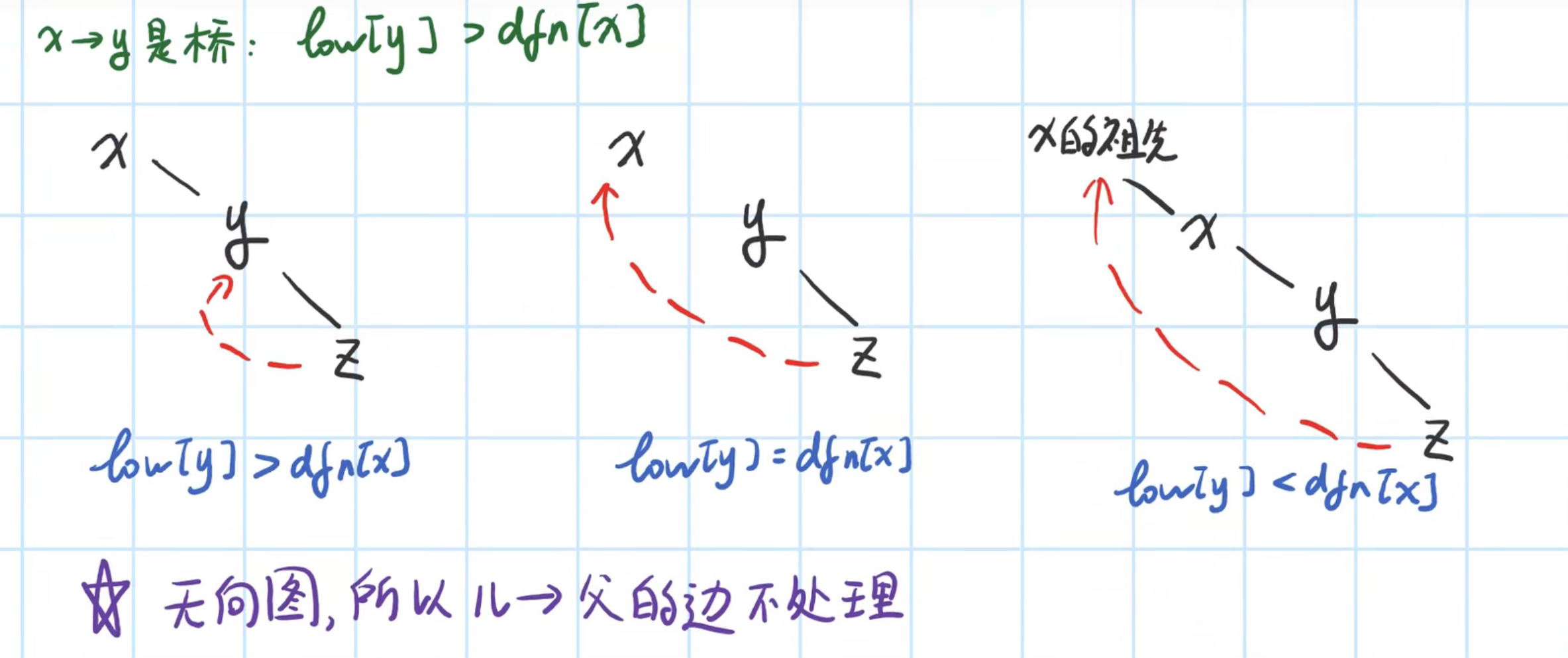
算法思路

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-ToHhZJVi-1647956663987)(https://s2.loli.net/2022/02/09/1JYAesvqpWLIU6y.png)]

代码-边

#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;

const int N = 5010, M = 20010;

int n, m;
int h[N], e[M], ne[M], idx;
int dfn[N], low[N], timestamp;
int stk[N], top;
int id[N], dcc_cnt;
bool is_bridge[M];
int d[N];

void add(int a, int b)
{
    e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}

void tarjan(int u, int from)
{
    dfn[u] = low[u] = ++ timestamp;
    stk[ ++ top] = u;

    for (int i = h[u]; ~i; i = ne[i])
    {
        int j = e[i];
        if (!dfn[j])
        {
            tarjan(j, i);
            low[u] = min(low[u], low[j]);
            if (dfn[u] < low[j])
                is_bridge[i] = is_bridge[i ^ 1] = true;
        }
        else if (i != (from ^ 1))
            low[u] = min(low[u], dfn[j]);
    }

    if (dfn[u] == low[u])
    {
        ++ dcc_cnt;
        int y;
        do {
            y = stk[top -- ];
            id[y] = dcc_cnt;
        } while (y != u);
    }
}

int main()
{
    cin >> n >> m;
    memset(h, -1, sizeof h);
    while (m -- )
    {
        int a, b;
        cin >> a >> b;
        add(a, b), add(b, a);
    }

    tarjan(1, -1);

    for (int i = 0; i < idx; i ++ )
        if (is_bridge[i])
            d[id[e[i]]] ++ ;

    int cnt = 0;
    for (int i = 1; i <= dcc_cnt; i ++ )
        if (d[i] == 1)
            cnt ++ ;

    printf("%d\n", (cnt + 1) / 2);

    return 0;
}

代码-点

#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;

const int N = 10010, M = 30010;

int n, m;
int h[N], e[M], ne[M], idx;
int dfn[N], low[N], timestamp;
int root, ans;

void add(int a, int b)
{
    e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}

void tarjan(int u)
{
    dfn[u] = low[u] = ++ timestamp;

    int cnt = 0;
    for (int i = h[u]; ~i; i = ne[i])
    {
        int j = e[i];
        if (!dfn[j])
        {
            tarjan(j);
            low[u] = min(low[u], low[j]);
            if (low[j] >= dfn[u]) cnt ++ ;
        }
        else low[u] = min(low[u], dfn[j]);
    }

    if (u != root) cnt ++ ;

    ans = max(ans, cnt);
}

int main()
{
    while (scanf("%d%d", &n, &m), n || m)
    {
        memset(dfn, 0, sizeof dfn);
        memset(h, -1, sizeof h);
        idx = timestamp = 0;

        while (m -- )
        {
            int a, b;
            scanf("%d%d", &a, &b);
            add(a, b), add(b, a);
        }

        ans = 0;
        int cnt = 0;
        for (root = 0; root < n; root ++ )
            if (!dfn[root])
            {
                cnt ++ ;
                tarjan(root);
            }

        printf("%d\n", ans + cnt - 1);
    }

    return 0;
}

一些结论

• 缩点后，形成一棵树，树有$cnt$个叶节点，则添加$\lfloor \frac{cnt+1}{2}\rfloor$个边，可使其变成双连通。

欧拉路径与欧拉回路

欧拉通路： 对于图G来说，如果存在一条通路包含G中所有的边，则该通路成为欧拉通路，也称欧拉路径。

欧拉回路： 如果欧拉路径是一条回路（可以从起点回到终点），那么称其为欧拉回路。

欧拉图 ： 含有欧拉回路的图是欧拉图。

判定

• 有向图
  • 欧拉路径： 图中所有奇度点的数量为0或2。
  • 欧拉回路： 图中所有点的度数都是偶数。
• 无向图
  • 欧拉路径： 所有点的入度等于出度 或者 存在一点出度比入度大1(起点)，一点入度比出度大1(终点)，其他点的入度均等于出度。
  • 欧拉回路：所有点的入度等于出度。

思路

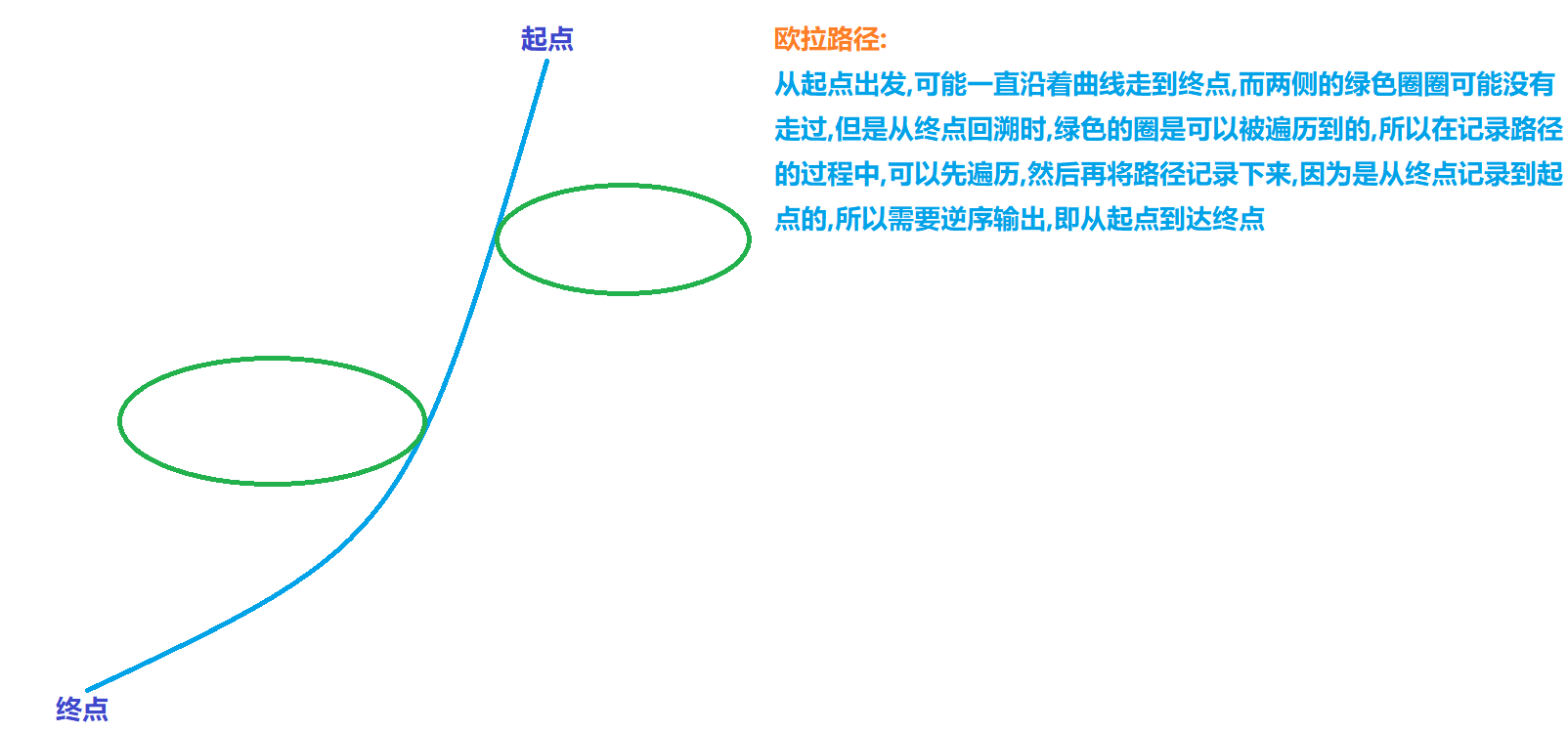
技巧

边的转化

无向图中的边的序号为:$0\sim 2m-1$,而在题目中的编号是$1\sim m$;

所以转化边时:0,1对应1号边,2,3对应2号边,即x号边对应x/2+1

其中偶数是正向边,奇数是反向边,可以用x^1转化正反向边的关系;

如果是奇数: x^1 中,x二进制前面的数不变,最后一位变成0,即 x^1 =x-1;

如果是偶数:x^1 中,x二进制前面的数不变,最后一位变成1,即 x^1=x+1;

搜索优化

代码：判定欧拉回路

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 100100, M = 400100;

int h[N],e[M],ne[M],idx;
int ans[N*2],cnt;
bool used[M];
int din[N],dout[N];
int n,m,ver;

void add(int a,int b){
    e[idx] = b,ne[idx] = h[a],h[a] = idx++;
}

void dfs(int u){
    for(int &i = h[u]; ~i; ){
        if(used[i]){  //如果这条边用过了
            i = ne[i];   //删除这条边
            continue;
        }

        used[i] = true;  //标记这条边已使用
        if(ver == 1) used[i^1] = true;   //如果是无向图，那么这条边的反向边也要标记使用过了

        int t;
        if(ver == 1){
            t = i/2 + 1;
            if(i&1) t = -t;  //(0,1) (2,3) (4,5) 奇数编号是返回的边

        }else t = i+1;

        int j = e[i];
        i = ne[i];
        dfs(j);
        ans[cnt++] = t;
    }
}
int main()
{
    scanf("%d%d%d",&ver,&n,&m);
    memset(h,-1,sizeof h);

    for(int i = 0; i<m; i++){
        int a,b;
        scanf("%d%d",&a,&b);
        add(a,b);
        if(ver == 1) add(b,a);  //无向边
        din[b]++, dout[a]++;   
    }

    if(ver == 1){
        for(int i = 1; i<=n; i++){
            if(din[i]+dout[i] &1){
                //无向图含欧拉回路的充要条件是每个点的度都为偶数
                puts("NO");
                return 0;
            }
        }
    }else{
        for(int i = 1; i<=n; i++){
            if(din[i] != dout[i]){
                //有向图含欧拉回路的充要条件是每个点的入度等于出度
                puts("NO");
                return 0;
            }
        }
    }

    for(int i = 1; i<=n; i++){
        if(~h[i]) {
            dfs(i);
            break;
        }
    }

    if(cnt < m){
        puts("NO");
        return 0;
    }

    puts("YES");
    for(int i = cnt-1; i>=0; --i){
        cout<<ans[i]<<" ";
    }
    return 0;
}

拓扑排序

用途

• 拓扑排序可以判断有向图是否存在环。我们可以对任意有向图执行上述过程，在完成后检查A序列的长度。 若 A 序列的长度小于图中点的数量， 则说明某些节点未被遍历，进而说明图中存在环。
• 求拓扑序

思路

不断选择入度为 0 的点 x，把 x 连向的点的入度 -1 。

代码

void topsort(){
    for(int i=1;i<=n;i++)
        if(!din[i])
            q.push(i);
    
    while(q.size()){
        int t=q.front(); q.pop();
        ans[++cnt]=t;
        for(int i=h[t];~i;i=ne[i]){
            int j=e[i];
            din[j]--;
            if(din[j]==0) q.push(j);
        }
    }
}

01规划

用处

在图论问题中，出现形如：
$$\frac{\sum f(i)}{\sum t(i)}的最大值$$
考虑使用01规划

思路

代码

#include <bits/stdc++.h>
#define endl "\n"
#define debug(x) cout << #x << ": -----> " << x << endl;
using namespace std;

const int maxn=5e5+10;
int e[maxn],ne[maxn],h[maxn],idx,wp[maxn],wseg[maxn];
double dis[maxn];
int cnt[maxn];
bool st[maxn];
int L,P;

void add(int a,int b,int c){
    e[idx]=b,wseg[idx]=c,ne[idx]=h[a],h[a]=idx++;
}

bool spfa(double mid){
    memset(st,0,sizeof st);
    memset(cnt,0,sizeof cnt);
    queue<int> q;
    for(int i=1;i<=L;i++){
        q.push(i);
        st[i]=true;
    }
    while(q.size()){
        int t=q.front(); q.pop(); st[t]=false;
        for(int i=h[t];~i;i=ne[i]){
            int j=e[i];
            // double v=j*mid
            if(dis[j]<dis[t]+wp[t]-mid*wseg[i]){
                dis[j]=dis[t]+wp[t]-mid*wseg[i];
                cnt[j]=cnt[t]+1;

                if(cnt[j]>=L) return true;

                if(!st[j]){
                    st[j]=true;
                    q.push(j);
                }
            }
        }
    }
    return false;
}

int main(){
    ios::sync_with_stdio(false); cin.tie(0); cout.tie(0);
    cin>>L>>P;
    for(int i=1;i<=L;i++) cin>>wp[i];

    memset(h,-1,sizeof h);
    for(int i=1;i<=P;i++){
        int a,b,c; cin>>a>>b>>c;
        add(a,b,c);
    }

    double l=0,r=1e7;
    while(r-l>1e-4){
        double mid=(l+r)/2;
        if(spfa(mid)) l=mid;
        else r=mid;
    }

    cout<<fixed<<setprecision(2)<<l;
    return 0;
}

树的直径

首先从树上任意一点开始搜索，BFS返回与该点距离最远点的编号$a_1$。

BFS搜索以该点$a_1$为起点，返回距离该点最远的点为$a_2$。

树的直径：$a_1-a_2$

直径的长度：$dis[a_2]$

代码

bool st[maxn];int dis[maxn];int bfs(int u){    memset(st,0,sizeof st);    memset(dis,0,sizeof dis);    queue<int> q;    st[u]=true;    q.push(u);    int res=0,max_dis=0;    while(q.size()){        int ver=q.front(); q.pop();        for(int i=h[ver];~i;i=ne[i]){            int j=e[i];            if(st[j]) continue;            st[j]=true;            dis[j]=dis[ver]+w[i];            q.push(j);            if(dis[j]>max_dis){                max_dis=dis[j];                res=j;            }        }    }    return res;}signed main(){    int l=bfs(1);    int r=bfs(l);    int len=dis[r];    return 0;}

树的深度

void dfs(int u,int fa){    size[u]=1;    for(int i=h[u];~i;i=ne[i]){        int j=e[i];        if(j==fa) continue;        dfs(j,u);        size[u]+=size[j];    }}

欧拉路径

欧拉路径: 经过图中每一条边恰好一次的路径

欧拉回路：起点和终点是同一个点的欧拉路径

DFS求欧拉路径。

在DFS的过程中，从一点开始DFS，后续搜索的过程中必然会返回到该点。

有向图欧拉路径

如仅判断，则无需存图。

bool st[];//int din[],dout[];int p[];int ans[];bool sol(){    int n; cin>>n;    for(int i=0;i<26;i++) p[i]=i;    for(int i=1;i<=n;i++){        string s; cin>>s;        int a=s[0]-'a',b=s[s.length()-1]-'a';        din[b]++,dout[a]++;        st[a]=st[b]=1;        p[find(a)]=find(b);    }    //除起点之外，其他点 入度==出度    int start=0,end=0;    for(int i=0;i<26;i++){        if(din[i]!=dout[i]){            if(din[i]==dout[i]+1) end++;            else if(din[i]+1==dout[i]) start++;            else{                return false;            }        }    }    if(!(end==0&&start==0||end==1&&start==1)) return false;    //孤立点判断    int anc=-1;    for(int i=0;i<26;i++){        if(st[i]){            if(anc==-1){                anc=find(i);            }            else if(anc!=find(i)){                return false;            }        }    }    return true;}

无向图欧拉路径

int idx;int d[maxn];int p[maxn];int find(int x){    if(x!=p[x]) p[x]=find(p[x]);    return p[x];}bool join(int a,int b){ //记录有效合并的次数    a=find(a),b=find(b);    if(a==b) return false;    p[a]=b;    return true;}int main(){    for(int i=0;i<=maxn;i++) p[i]=i;    int cnt=0;    string s1,s2;    while(cin>>s1>>s2){        int a=get(s1),b=get(s2);        d[a]++,d[b]++;//度++        if(join(a,b)) cnt++;    }    if(cnt<idx-1){//有效合并次数小于节点数-1，则有剩余点        cout<<"Impossible"<<endl;        return 0;    }    cnt=0;//记录奇数边的数目    for(int i=1;i<=idx;i++){        if(d[i]&1){            cnt++;            if(cnt>2){                cout<<"Impossible"<<endl;                return 0;            }        }    }    cout<<"Possible"<<endl;    return 0;}

并查集找最小环

二分图

染色法

int color[];bool dfs(int u,int c){    color[u]=c;    for(int i=h[u];~i;i=ne[i]){        int j=e[i];        if(color[j]){            if(color[j]==c) return false;        }        else if(!dfs(j,3-c,mid)) return false;    }    return true;}

匈牙利算法

有向图

#include <bits/stdc++.h>using namespace std;int m, n1, n2;const int maxn = 1e5 + 10, N = 510;int e[maxn], ne[maxn], h[N], idx;bool st[N];int match[N];void add(int a, int b);bool find(int x){    for(int i = h[x]; i != -1; i = ne[i]){        int j = e[i];        if(st[j]) continue;        st[j] = true;        if(match[j] == 0 || find(match[j])){            match[j] = x;            return true;        }    }    return false;}int main(){    cin >> n1 >> n2 >> m;    memset(h, -1, sizeof h);    for(int i = 0; i < m; i ++){        int u, v; cin >> u >> v;        add(u, v);    }    int cnt = 0;    for(int i = 1; i <= n1; i ++){        memset(st, false, sizeof st);        if(find(i)) cnt ++;    }    cout << cnt;    return 0;}

方格图是二分图

bool find(int x,int y){    for(int i=0;i<8;i++){        int xx=x+dx[i],yy=y+dy[i];        if(xx>=1&&xx<=n&&yy>=1&&yy<=m&&!g[xx][yy]&&!st[xx][yy]){            st[xx][yy]=1;            auto t=match[xx][yy];            if(t.first==-1||find(t.first,t.second)){                match[xx][yy]={x,y};                return true;            }        }    }    return false;}

最大匹配数：最大匹配的匹配边的数目

最小点覆盖数：选取最少的点，使任意一条边至少有一个端点被选择

最大独立数（集）：选取最多的点，使任意所选两点均不相连

最小路径覆盖数：对于一个 DAG（有向无环图），选取最少条路径，使得每个顶点属于且仅属于一条路径。路径长可以为 0（即单个点）。

定理1：最大匹配数 = 最小点覆盖数（这是 Konig 定理）

定理2：最大匹配数 = 最大独立集

定理3：最小路径覆盖数 = 顶点数 - 最大匹配数

最大匹配

二分图中，最大匹配的边的数量。

• 0要素：节点能分成独立的两个集合，每个集合内部有0条边
• 1要素：每个节点只能与一条匹配边相连

最小点覆盖

选取最少的点，使任意一条边至少有一个端点被选择。等于$cnt$

• 2要素：每条边有两个端点，二者至少选择一个。

最小路径点覆盖

给定一张有向无环图，要求用尽量少的不相交的简单路径，覆盖有向无环图的所有定点（也就是每个顶点恰好被覆盖一次）。等于$n-cnt$

最小路径重复点覆盖

给定一张有向无环图，从中选出最多的点，使得任意两点之间互不相通。等于$n-最小路径重复点覆盖$

树型DP

树的直径（树的最长路径）

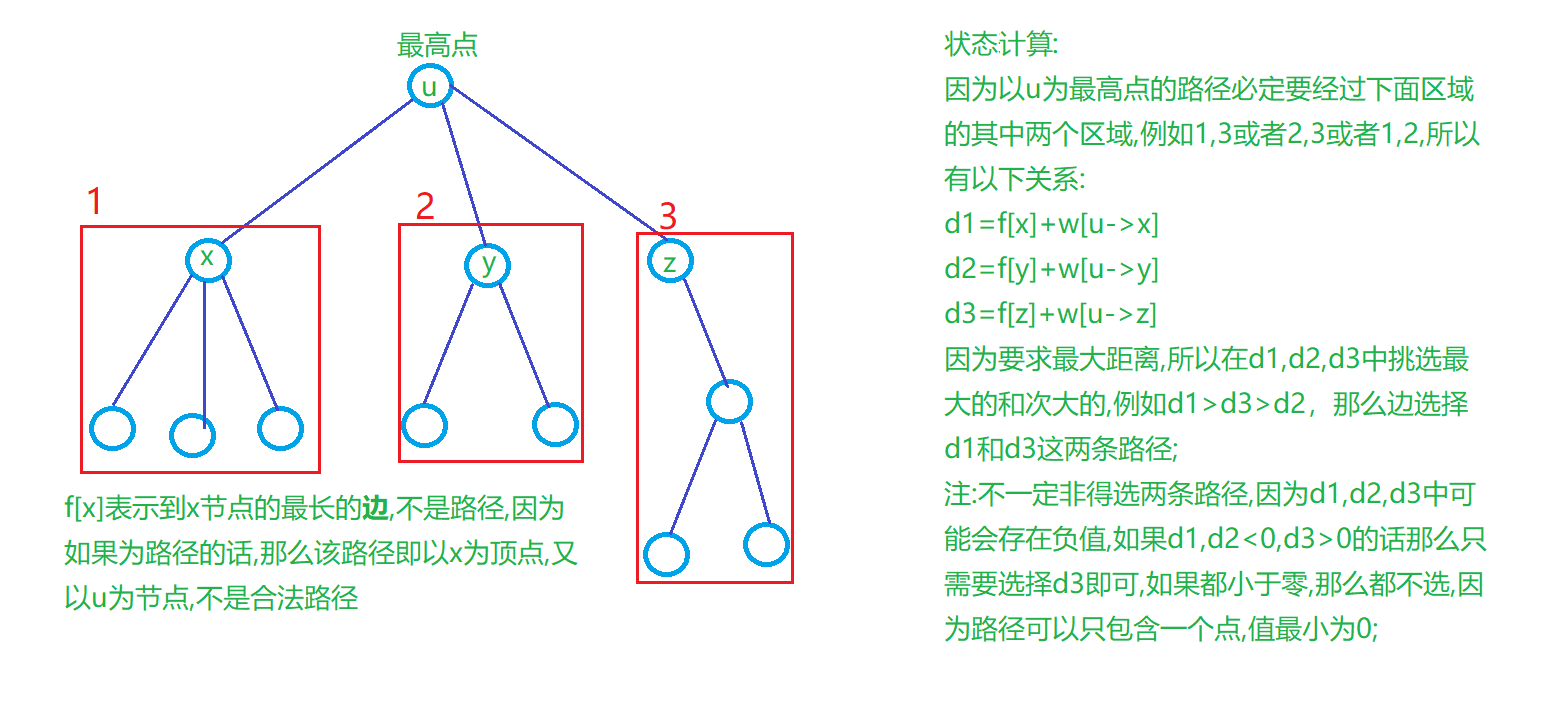
int dfs(int u,int fa){    int dist=0;    int d1=0,d2=0;    for(int i=h[u];~i;i=ne[i]){        int j=e[i];        if(j==fa) continue;        int d=dfs(j,u)+w[i];        dist=max(dist,d);        if(d>=d1) d2=d1,d1=d;        else if(d>d2) d2=d;    }    ans=max(ans,d1+d2);    return dist;}

树的中心

树的最大连通块

Floyd

传递闭包

void floyd() //通过floyd来逐渐更新每两个点的连通情况{    memcpy(d, g, sizeof d);    for(int k = 0; k < n; k ++)       for(int i = 0; i < n; i ++)           for(int j = 0; j < n; j ++)            d[i][j] |= d[i][k] & d[k][j];            //if(!d[i][j]) d[i][j] = d[i][k] & d[k][j];              }

最小环

最小生成树