本文介绍了如何使用混沌理论和混沌2.0工具箱在MATLAB上进行混沌序列的识别和分析。通过二维相图展示混沌奇异吸引子进行定性识别，再用饱和关联维数法进行定量分析，揭示混沌序列的特性。此外，还提及了基于最大Lyapunov指数的混沌时间序列预测方法，并提供了相关MATLAB代码资源。
本文是基于混沌理论，利用混沌2.0工具箱，在MATLAB上进行计算，感谢原作者的努力奉献，参考文献另附。
以X变量的时间序列为研究对象，进行时空演变分析，通过定性与定量进行识别。
- 定性分析以二维相图法，绘制出混沌奇异吸引子，进行特异性识别。
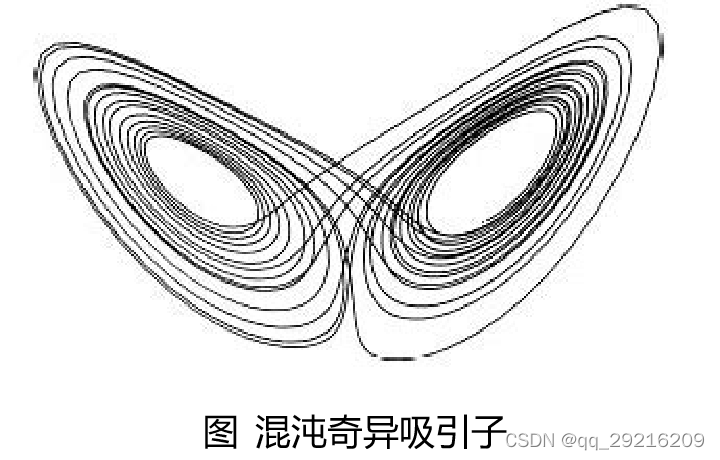
结果如上图，此混沌序列为单吸引子，可见相轨迹均存在着一个以单个吸引子为中心的吸引域，各相点的运动不断回复、折叠，不断地靠近和远离吸引域，这表明它们均存在着混沌特性。
- 定量分析采用饱和关联维数法进行定量识别
绘制不同嵌入维数条件下的lnr0-lnC(r)关系图，从图中可以直观地看到，若lnr0与lnC(r)的曲线中包含一部分直线，那么这条直线的斜率就称之为关联维数dm，如果时间序列中存在奇异吸引子，那么随着嵌入维数m的增加，关联维数dm也会增加，当关联维数增加到一定值以后，得到的饱和值D即时间序列的饱和关联维数。
饱和关联维数dm越大，混沌特性就越强；饱和关联维数越小，混沌特性就越弱。
以上是混沌序列的识别阶段
混沌理论也可以进行时间序列的预测（如基于最大Lyapunov指数的预测方法）
感兴趣的可以用代码包试一试
混沌计算MATLAB代码
https://download.csdn.net/download/qq_29216209/79087380
扫一扫
2万+
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
