说明
在IEEE标准中,浮点数在内存中的表示是将特定长度的连续字节的所有二进制位按特定长度划分为符号域,指数域和尾数域三个连续域。
float
float类型在内存中占用的位数为: 1+8+23=32bits
double
1+11+52=64bits
第一位s代表符号为,1代表负数,0代表正数。
第二个域是指数域,对于单精度float类型,指数域有8位,可以表示 0-255个指数值。指数值规定了小数点的位置,小数点的移动代表了所表示数值的大小。但是,指数可以为正数,也可以为负数。为了处理负指数的情况,实际的指数值按要求需要加上一个偏差(Bias)值作为保存在指数域中的值,单精度数的偏差 值为 -127,而双精度double类型的偏差值为 -1023。比如,单精度指数域中的64 则表示实际的指数值 -63。 偏差的引入使得对于单精度数,实际可以表达的指数值的范围就变成-127 到 128 之间(包含两端)。我们不久还将看到,实际的指数值-127(保存为 全 0)以及 +128(保存为全1)保留用作特殊值的处理。这样,实际可以表达的有效指数范围就在 -126 和 +127 之间。
第三个域为尾数域,其中单精度数为 23 位长,双精度数为 52 位长。比如一个单精度尾数域中的值为: 00001001000101010101000, 第二个域中的指数值则规定了小数点在尾数串中的位置,默认情况下小数点位于尾数串首位之前。
比如指数值为 -1,则该float数即为:.000001001000101010101000,如果为+1,则该float 数值为:0.0001001000101010101000。我们知道引入浮点数的目的在于用尽可能少的位数表示既高精度又大范围的实数,其中的范围大小是由指数域位长确定的,而尾数域的长度则确定了所能表示实数的精度,所以double比float数的精度更高,范围更大,相应的也就占用更多的内存。 刚才我们介绍的对尾数域中的值的解释并不能实现这个精度最大化的目标,因为在尾数串第一个”1”之前还有4个”0”,这4个”0”实际上是多余的,因为我们把小数点向前移动时,前端的"0"是自动添加的,所以可以把这4个“0”删除,然后尾数域末端多出4个位来表示更高精度的数值。也就是说尾数的第一位一定是"1",那么既然第一位一定是"1",那么我们也就没有必要把它存储在尾数域中,而是直接默认尾数为1.xxxx…xxx的形式。尾数的首位从小数点后开始。那么上面的例子所表示的尾数就是:
1.00001001000101010101000。 用23位表示了24位的信息 (小数点不占位置).
表示
一个规格化的32位浮点数x的真值为:
x=(−1)^s × (1.M) × 2^E−127
一个规格化的64位浮点数x的真值为:
x=(−1)^s × (1.M) × 2^E−1023
下面举一个32位单精度浮点数-3.75表示的例子帮助理解:
(1) 首先转化为2进制表示
−3.75=−(2+1+1/2+1/4)=−1.111×2^1
(2) 整理符号位并进行规格化表示
−1.111×21=(−1)(1)×(1+0.1110 0000 0000 0000 0000 000)×2^1
(3) 进行阶码的移码处理
(−1)^(1)×(1+0.1110 0000 0000 0000 0000 000)×2^1
=(−1)^(1)×(1+0.1110 0000 0000 0000 0000 000)×2^128−127
于是,符号位S=1,尾数M为1110 0000 0000 0000 0000 000阶码E为128_10=1000 0000_2,则最终的32位单精度浮点数为1 1110 0000 0000 0000 0000 000 1000 0000
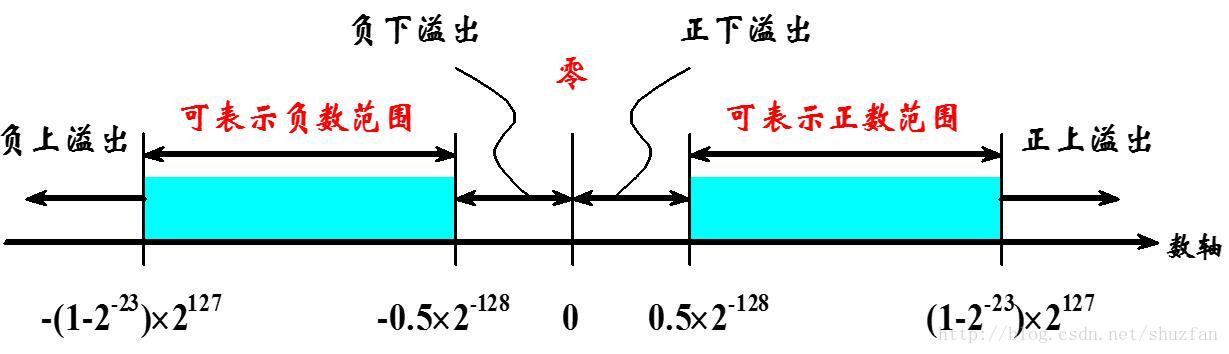
浮点数表示范围与精度
通过上面的规格化表示,我们可以很容易确定浮点数的表示范围:
一般提到浮点数的精度(有效位数)的时候,总是会出现 float的有效位为6~7位, double的有效位为15~16位 。
既然有表示范围,那肯定也有不能表示的数值:
下面以float为例,解释一下有效位数是怎样来的。
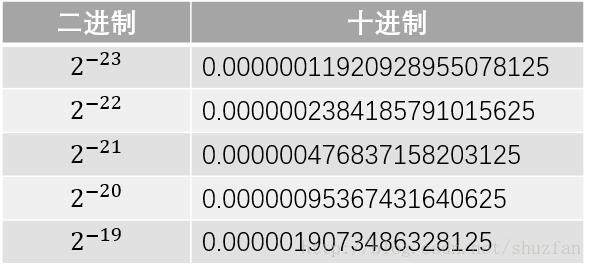
有效位数只和规格化浮点数的尾数部分有关,而尾数部分的位数是23位,因此我们首先列出下表
由上面的表格可以看出:
2−23 和 2−22 之间是存在间隔的,即0.0000001和0.0000002之间的小数我们是没有办法描述的,因此23位尾数最多只能描述到小数点后第7位;此外,我们通过四舍五入可以很容易发现0.0000003=0.0000004=2−23+2−22, 这表明第7位有效数字只是部分准确。而第6位及之前的都是可以准确描述的,因此我们说float的有效位为6~7位。
例子
参考资料:

























 6万+
6万+











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








