目录
一.浮点数的表示
1.浮点数的作用和基本原理
定点数在字节数固定的情况下,能表示的数字是很有限的,但我们不能无限制地增加数据的长度(2bit-->4bit-->8bit)。在位数不变的情况下增加数据表示范围,就是浮点数的作用。
浮点数的结构:
浮点数分为阶码和尾数两个部分,以科学计数法为例,11为阶码,表示10的11次方,+3.026是尾数。

如下图所示,阶码由阶符和数值部分组成。阶符为正表示需要将小数点后移,阶符为负表示需要将小数点左移。数值部分表示需要移动多少位。阶码常用补码或移码表示的定点整数。
尾数由数符和尾数的数值部分组成,数符表示数值的正负,数值部分表示数值的大小,尾数的数值部分长度越短,科学计数法能表示的数字精度越低。尾数常用原码或补码表示的定点小数。

补充:
长度相同,格式相同的两种浮点数,前者基数大,后者基数小,其他规定均相同,则它们可表示的精度和范围:基数大的浮点数能表示的范围更大,精度更低,基数小的浮点数反之。
原因:
拿2^n和4^n,为例,4^n=
,阶码每变化1位,需要移动的位数为2位,而2^n,阶码每变化一位,只需要移动1位。所以基数越大,阶码每变化一位,尾数小数点需移动的位数越多,能表示的数的绝对值越大。
基数越大,相邻两个浮点数之间的间隔就越大,精度越低。
所以,阶码E反映浮点数的表示范围及小数点的实际位置;尾数M的数值部分的位数n反映浮点数的精度。尾数给出一个小数,阶码指明了小数点要向前/向后移动几位。
浮点数的表示:
之前学习的定点数,小数的小数点默认隐含在符号位后,整数的小数点默认隐含在数值最后。由于小数点的位置固定不变,所以称为定点,而现在学习的浮点数,小数点的位置是会浮动的。具体的位置与阶码有关。二进制浮点数的真值:
以十进制作类比:
E表示阶码;M表示尾数;r表示阶码的底数(默认阶码的底数为2,也可以取4,取8),10进制中阶码的底数为10,二进制中阶码的底数是2。当阶码为1时,尾数*2^1,就表示将其小数点后移一位,也可以说让尾数算术左移一位。
![]()
使用8bit的空间刚好能存储a这个浮点数:

对于浮点数b:![]()
浮点数b阶码占3位,尾数部分占6位,如果依旧用8bit的存储空间存储,则尾数最后1位会被抛弃。如果把最后1个"1"抛弃了,那么这个浮点数的精度就降低了。
![]()
所以,如何在存储空间不变的情况下,尽可能保留浮点数的精度,这就需要对浮点数进行规格化。
2.浮点数的规格化
以科学计数法为例,我们规定在科学计数法中,只能使用4个数字表示尾数部分,那么一个浮点数的表示方式很多,区别就在于每个浮点数的精度不同。
![]()
其实,科学计数法会规定尾数的最高位必须为有效值,如果最高位是无效值,则会丧失精度。
现在把这种思想推移到二进制的浮点数表示。在上面的例子中,b=0,10;0.01001,尾数的第1个"0"表示符号位,必须保留;而小数点后的第1位为"0",表示这是一个无效值,所以将尾数部分算术左移一位,或者说让小数点向右移动1位,并且将阶码减1。

上面的操作也称为"左规",即通过算术左移的方法,直到尾数最高数值位是有效值,使得浮点数规格化。相对的,也有"右规"。拿10进制举例,数字302.6*10^9,经过规格化后,变为3.026*10^11,即尾数右移两位,阶码加2。
总结:
规格化浮点数:规定尾数的最高数值位必须是一个有效值。
左规:当浮点数运算的结果为非规格化时要进行规格化处理,将尾数算数左移一位,阶码减1。右规:当浮点数运算的结果尾数出现溢出(双符号位为01或10)时,将尾数算数右移一位,阶码加1。
补充:
若浮点数的基数是4,尾数用原码表示,则规格化小数需要小数点后2位不全为0。
例如,1.011011,小数点前面为符号位,小数点后为01,不全为0。
举个例子:
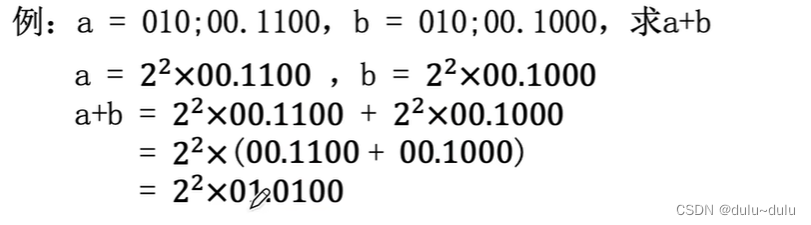
在上面例子中,尾数为01.0100,双符号位为01,发生溢出需要进行"右规",将尾数右移1位,使得这个位置的数字和双符号位的第1个符号位保持一致,再将阶码+1。

经过"右规"后,尾数为00.1010,其最高数值位为有效值,说明这是一个规格化的浮点数。
可以看到,若采用"双符号位",当发生溢出时,更高的符号位是正确的符号位,可以通过"右规"将浮点数进行恢复。正是因为采用"双符号位"可以挽救某些溢出的情况,所以采用"双符号位"判断是否溢出是现实中最长被应用的。
规格化浮点数的特点:
浮点数的尾数通常会使用原码或补码表示,当采用不同方式表示尾数,"数值最高位到底为多少才算有效值"是有区别的:
1.用原码表示的尾数进行规格化:
正数为0.1xx...x的形式,其最大值表示为0.11...1;最小值表示为0.10...0。即保证数值位最高位是1。尾数的表示范围为
负数为1.1xx...x的形式,其最大值表示为1.10...0;最小值表示为1.11...1。尾数的表示范围为
可以发现,规格化的原码尾数,最高数值位一定是1。
2.用补码表示的尾数进行规格化:
正数为0.1xx...x的形式,其最大值表示为0.11...1;最小值表示为0.10...0。尾数的表示范围为
负数为1.0xx...x的形式,其最大值表示为1.01...1:最小值表示为1.00...0。尾数的表示范围为
这里的负数可以用-1/32和-1进行理解,小数点后面1越多,绝对值越小,加上负号后,绝对值越小的数反而越大。也可以记,真值越大,补码尾数越大,真值越小,补码尾数越小。
我们可以发现一个规律:
若浮点数用补码表示,数符与尾数小数点后第1位数字相异为规格化数。
举个例子:
![]()
尾数为1.1110100,由于使用补码表示,尾数应为1.0xx....x才是规格化的浮点数,所以将补码算数左移进行“左规”:
注:补码负数算数左移,低位补0;补码负数算数右移,高位补1。
将1.1110100,算数左移3位,得到1.0100000,每左移一次,阶码减1,左移3位,阶码减3(0.110=6 ,6-3=3=0.011)。最后得到规格化浮点数为:0.011;1.01000000
3.浮点数的表示范围
虽然浮点数的表示范围比同长度的定点数大得多,但是也会出现溢出的情况:如果超出了正数所能表示的最大范围,称为“正上溢”,超出负数所能表示的最大范围,称为"负上溢"。如果遇到这两种情况,通常会抛出系统异常,表示运算结果溢出。
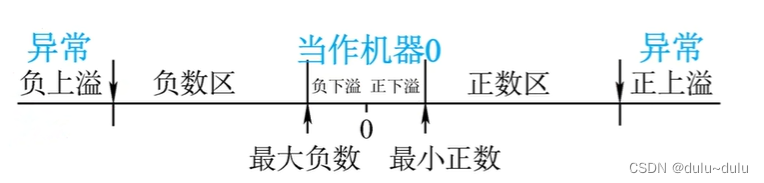
对于规格化之后的尾数,所能表示的最小的数为0.1,记1/2。如果此时阶码为3位,并且用补码表示,3位的补码整数所能表示的最小的数为-4(),所以对于阶码为3的浮点数,其能表示的最小正数为1.00;0.1=0.00001,如果想要表示的数小于0.00001,那么就会发生"正下溢","负下溢"的原理相同。当出现这两种情况,我们通常会将这个数当作机器数0处理。

二.IEEE 754标准
上节说到阶码通常可以用补码,移码表示,尾数通常用补码,原码表示。只有确定一个标准,即阶码和尾数各自用什么码,取多少位,各计算机之间才能通过这一标准进行浮点数的交换。所以出现了IEEE 754标准。
在IEEE754中,阶码是用移码表示的,移码就是在补码的基础上将符号位取反。
注意:移码只能用于表示整数,由于浮点数的阶码部分也是用整数表示的,所以移码可以用来表示阶码。
移码=真值+偏置量(偏置值一般取,此时移码=补码符号位取反),此处8位移码的偏置值=128D=1000 0000B,即
,对于真值-127而言,其移码表示为:
真值-127=-1111111B,移码= -1111111+1000 0000=0000 0001
所以-127的移码为0000 0001。
以下转换同理:
![]()
在IEEE 754中,其偏移量为127D=0111 1111B,即:

01111111+(-1000 0000),在上面的例子中,偏置值比-128的绝对值小,那么这个加法操作怎么做呢?
由于移码是8bit,所以所有的加减运算在背后都会默认进行,在
这个条件下进行加减法时,可以在原有的基础上再加上2^8(100000000),加上这个值后,减法得到的值是不变的。可以打个比方来理解,钟表上有12个小时,求早上7点到下午5点之间有几个小时,5是被减,7是减数,5加周期12才能减7。
加上2^8后就可以计算了,得101111111+(-1000 0000)=1111 1111,所以在偏置值为127的情况下,-128所对应的移码是1111 1111。如下图所示,当偏置值为时,将得到的移码看作无符号数,从无符号数1~无符号数254,随着无符号数的逐步递增,移码的真值也是逐步递增的。
还要记住8位移码能表示的范围是-128~127,在偏置值为127的情况下,-128的移码为1111 1111,-127的移码为0000 0000。IEEE 754标准中,全1和全0都有特殊的用途,所以8位阶码真值范围其实是-126~127。
![]()
以同样的方法计算,可得其他真值的移码如下:
![]()
IEEE 754标准中规定的浮点数格式如下,对于以下浮点数的数符,阶符,尾数数值的位数一定要记住,考试的时候不会给出:
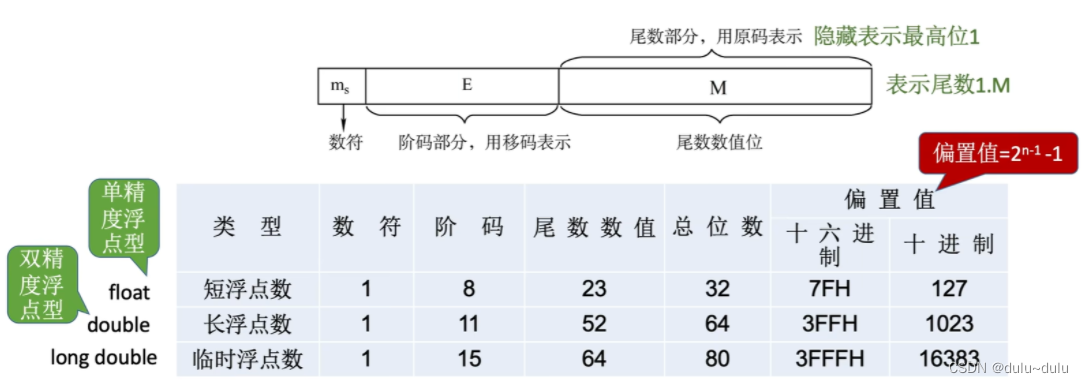
对于短浮点数:
其数符"1"表示这个浮点数是一个负数,蓝色的这8位表示阶码,阶码是用移码表示的,所以移码=000 0001 1,移码=真值+偏置值,所以真值=移码-偏置值,对于短浮点数而言,就是-127
因此短浮点数的真值:
(-1)^s用于确定正负性,1.M表示1.尾数,对于短浮点数而言就是"1"+"后面的23位",最后*
E-127就是“移码-偏置值”
对于长浮点数:
1为数符,000 0001 1100表示阶码,后面的52位表示尾数数值,前面隐含"1."
在计算的时候可以把移码部分和偏置值部分看作无符号数进行相减操作,不一定要用两个二进制数相减。例如上面的例子,移码=000 0001 1100=28,28-1023=-995,-995就是阶码真值。
看下面的例题:
1.

① 首先确定单精度浮点数包括1位数符,8位移码,23位尾数。
② 将10进制数转化为规格化的二进制数。
③ 从规格化二进制数中可以看到以下信息,单精度浮点型偏移量为127D,阶码用移码表示,所以需要将阶码真值转换为移码,移码=阶码真值+127=-1+127=126=0111 1110(凑足8位)
④ 按数符,移码,尾数的顺序写出单精度浮点数:
2.

① 将16进制数转换为与之对应的二进制数:
② 从2进制数中可以得到信息:
③ 单精度浮点数的偏移量是127D,所以阶码真值=移码-偏移量=129-127=
④ 所以浮点数的真值:
IEEE 754 精度浮点型能表示的最小绝对值、最大绝对值是多少?

最小绝对值: 尾数全为0(隐含最高位1),阶码真值最小-126,对应移码机器数0000 0001(-126+127=1=0000 0001),此时整体的真值为:

最大绝对值:尾数全为1,阶码真值最大127,对应移码机器数 1111 1110(127+127=254=1111 1110),此时整体的真值为:

1.111...11=1+1/2+1/4....,是一个以1/2为公比的n=24的等比数列:
用类似的方法计算双精度浮点数的最小绝对值和最大绝对值,得到:

若要表示的数绝对值还要更小,怎么办?
这就需要用到阶码"全1"和"全0"的两个状态:对于单精度浮点数而言,阶码总共占8bit,如果将其看作无符号数,那么他所能表示的范围就是0~255,0对应的就是"全0"的二进制,255对应的"全1"是全1的二进制,![]() ,这里的
,这里的,是将移码解读为无符号数得到的,当我们将其分别减偏移量127,就能得到真值的表示范围(-126~127)
① 当阶码E为全0,尾数M不全为0时,表示非规格化小数:
如果我们想存储单精度浮点数0.001*2^-126,那么我们可以使数符位为0,阶码部分全为0,尾数部分为001后面跟20个0(尾数部分总共23位,最高位隐含0)。
所以使用阶码全为0这个特殊值,那么就可以用单精度浮点数表示比最小绝对值还要小的数。
虽然在偏置值为127时,移码的全0对应的真值是-127,但在这里将阶码真值固定为-126,记住就好。
② 当阶码E全为0,尾数M全为0时,表示真值
,具体是+0还是负0,看数符即可。
③ 当阶码E全为1,尾数M全为0时,表示无穷大
,是正是负同样看数值部分,但我们对两个浮点数进行加法时,如果发生了"正上溢"或"负上溢",机器通常会把结果记录为+
,-
④ 当阶码E全为1,尾数M不全为0时,表示非数值"NAN"(Not a Number),如:0/0、
等非法运算的结果就是 NaN。
三.浮点数的加减运算
1.加减运算
浮点数的加减会经过以下几个步骤,先拿10进制的运算举例:
① 对阶 ② 尾数加减 ③ 规格化 ④ 舍入 ⑤ 判溢出
① 对阶:小阶向大阶对齐。为什么要这样处理,原因是计算机内部的尾数是定点小数,如果让大阶向小阶对齐,例如将9.85211*10^12---->985.211*10^10,那么小数点前面就会有很多有效位,这种转换对于计算机而言很难实现,而用小阶向大阶对齐,例如:
9.96007*10^10--->0.0996007*10^12,那么计算机需要做的只是算术右移。所以使用小阶向大阶对齐是为了方便计算机对尾数进行处理。
![]()
② 尾数相加:
![]()
③ 规格化:保证尾数的第1个数值位为有效位。
![]()
④ 舍入:
由于计算机中尾数的比特位长度有限,例如单精度浮点数尾数的bit位长度为23,双精度浮点数尾数的bit位长度为52。将两个浮点数相加时,新得到的浮点数可能长度过长,所以需要进行"舍入"。
![]()
所以可以用不同的舍入规则。
⑤ 判溢出:
对于计算机而言,阶码的位数是固定不变的,如果结果的阶码部分超出了浮点数能表示的范围,那么就说明发生了溢出。
用10进制数类比就是:
将这个步骤迁移到二进制,思路也是相通的:

首先用补码表示阶码和尾数。
将这两个数用二进制表示:
再分别转变为补码:
尾数-0.101,阶码2^-101:
对于2^-101,-101的补码为1011,双符号补码为11011
对于尾数-0.101,补码为1.011,尾数的数符需要取两位,所以双符号补码为11.011,由于尾数取9位,所以需要进行拓展,得11.011000000。
对于Y同理:
① 对阶
需要小阶向大阶对齐,计算机是怎么判断谁的结束更小的呢?只需要进行相减的操作,也就是[X]补-[Y]补=[X]补+[-Y]补,[Y]补-->[-Y]补=00100。11111(补码)中的前2位为双符号位,即
11,111(补码)--->11,001(原码)=-1。
由于X的阶数更小,比Y的阶数小1位,所以需要让X的尾数向右移一位(注意:尾数是负数补码,右移补1,正数补码,右移补0),尾数每向右移一位,X的阶码+1。
阶码为11100,即11,100,2^-100=2^-4
尾数为11.1011(补码)--->11.0101(原码)-->-0.0101
注意:这一步进行了右规操作,所以可能需要舍入。
② 尾数加减
由于双符号位数值不同,说明发生溢出:(01负溢出,10正溢出)
为什么呢?结合之前计算的X,将X-Y,可以得到尾数的值大于1了,由于定点小数没办法表示大于1的数,所以溢出了。
③ 规格化:之前讲过,可以通过"右规"的方式,挽救溢出:算术右移,高位补1/0,具体看符号位是什么,末尾的1位会被抛弃。别忘了尾数右移,阶码+1。最后得到:
手算的话,相当于进行了下面一步:阶码由-4变为-3
④ 舍入:刚刚抛弃了最后1位0,对精度没有任何影响,所以不需要进行舍入。
⑤ 判溢出:没有溢出,真值为
•若某浮点数需要舍入,通常可以使用以下两种方法:
1.“0”舍“1”入法:类似于十进制数运算中的“四舍五入”法,即在尾数右移时,被移去的最高数值位为0,则舍去;被移去的最高数值位为1,则在尾数的末位加1。注意:这样做可能会使尾数又溢出,此时需再做一次右规。
例如下图,规格化步骤中,进行"右规"的时候,末尾被舍去一个1,所以在“新的末尾”加1,01+1=10。如果舍弃的末尾为0,直接舍弃即可,不用进行其他操作。

2.恒置“1”法:尾数右移时,不论丢掉的最高数值位是“1”还是“0”。都使右移后的尾数末位恒置“1”。这种方法同样有使尾数变大和变小的两种可能。
例如下图,不论最后末位舍弃的是什么值,只要将其末位置为1即可。

进行规格化和舍入时,阶码的值会发生改变,如果阶码的值超出上限,就说明发生了某种上溢,具体是正上溢还是负上溢,得看尾数的数符是正还是负。而阶码的值低于下限,就会发生x下溢,发生下溢,会当作机器0处理,并不会当作一种错误,而上溢则会判定为一种异常。
![]()
补充:除了右规(对阶和规格化阶段都出现了右规,都有可能需要舍入)会出现舍入的问题,下面这种情况也需要进行舍入。
有的计算机可能会把浮点数的尾数部分单独拆出去计算,例如,对于float型变量,就是将24bit的尾数(1为隐含的最高位,23位为显式表示的尾数),用32bit的变量保存,这样尾数右移,就不会导致精度丢失,因为可以用多余的bit位存放。经过规格化后,还需要进行舍入,就是将32bit重新截断为24bit,再拼回float浮点数中。
•定点运算判溢出和浮点运算判溢出的区别:
在定点运算中,当运算结果超出数的表示范围时,就发生溢出;
在浮点运算中,运算结果超出尾数表示范围却不一定溢出,可能仅产生误差。只有规格化后阶码超出所能表示的范围时,才发生溢出。
并且浮点数运算是否溢出,取决于阶码是否上溢,因为阶码下溢可以通过非规格化数来表示,这样即使出现了比最小规格化数还小的数,程序也能进行。
注意:只有进行了右规操作,阶码+1才有可能发生溢出,对于"对阶"操作,虽然进行了"右规"操作,但是他是小阶向大阶对齐,所以绝对不会发生溢出。
补充:非规格化数,隐藏位为0,且单精度和双精度浮点数的指数分别为-126和-1022。
2.强制类型转换
虽然现在计算机都是64位机器,但是在考试中,考察强制类型转换,还是会按照32位机器各个变量的长度进行考察。

从bit位长度小的类型到bit位长度大的类型的强制类型转换都是无损的转换:数据的精度不会丢失,表示范围也不会缩小。

long-->double:
long型有32位bit位,而double型尾数为52位,再加上隐含的最高位1,实际尾数有53位,53位可以表示32位的数能表示的任何精度,所以由long-->double的强制类型转换不会丢失精度,是无损转换,但是如果题目所叙述的long型变量为64位,那么long-->double就会产生精度的损失。
int-->float:
对于int:int表示整数,他有1个符号位和31个有效数值位,所以表示的范围:~
,有效数字32位。

1位隐含的最高位1+23位显式的尾数=24。所以int型转float型肯定会有精度损失,考虑上float型的8位阶码,他所能表示的数的范围肯定比int型更大,所以int型转float型会有精度损失,但是不会出现溢出,转换为double型则能保留精度。反过来float型或double型转int型,既可能发生溢出,也可能产生精度损失。

例如,float型变量可以表示小数0.000111,将其转化为int时,会将小数点后的数全部截断,只保留整数。
总结:













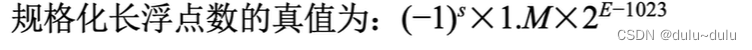


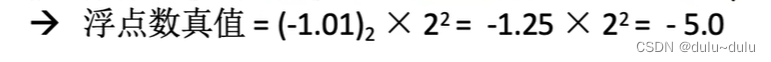





















 14万+
14万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








