第十二届蓝桥杯软件类 C/C++ A组 个人解答（基本完结）

已于 2023-02-03 16:15:13 修改
阅读量3.2k 收藏 52
点赞数 11
分类专栏： C++ 蓝桥杯 文章标签： 算法 c++ 动态规划 数据结构
于 2021-04-19 23:20:44 首次发布
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/qq_29353083/article/details/115863767
版权

目录

A：卡片

题目
在这里插入图片描述
答案：3181

#include <iostream>

using namespace std;

const int N=100;

int n;
int st[N];

int split(int n)
{
    while(n)
    {
        if(--st[n%10]<0) return false;
        n/=10;
    }
    return true;
}

int main()
{
    n=2021;
    for(int i=0;i<10;i++) st[i]=n;

    int i=1;
    while(split(i)) i++;

    cout<<i-1<<endl;

    return 0;
}

B：直线

题目
在这里插入图片描述
题解

  • 常规思路用斜率，但这里斜率相同的可能也是不同的直线，由此我们可以存一下该斜率在 y 轴上的截距，就能唯一判断了
  • 特殊处理 x 1 − x 2 = 0 x1-x2=0 x1−x2=0 的点（斜率为无穷）：直接加上竖线条数即可
  • 也可以先弄出所有直线，排个序方便去重一些，这里就不写了

答案： 40257

#include <iostream>
#include <cmath>

using namespace std;

const int N=1000010;
const double eps=1e-6;

int n,m;
double st[N],d[N];
int cnt;

bool check(double k,double t)
{
    for(int i=0;i<cnt;i++)
    {
        if(abs(st[i]-k)<eps&&abs(d[i]-t)<eps) return false;
    }
    d[cnt]=t;
    st[cnt++]=k;
    return true;
}

int main()
{
    //n=20,m=21;
    //n=3,m=4; //35
    //n=2,m=3; //11
    cin>>n;
    m=n+1;

    int res=0;
    for(int x1=0;x1<n;x1++)
        for(int y1=0;y1<m;y1++)
            for(int x2=0;x2<n;x2++)
                for(int y2=0;y2<m;y2++)
                {
                    if(x1==x2) continue;
                    double dx=x1-x2,dy=y1-y2;
                    double k=dy/dx;
                    if(check(k,y1-k*x1)) res++;
                }
    cout<<res+n<<endl;
    return 0;
}

C：货物摆放

在这里插入图片描述
答案：2430

算法1： 枚举约数法，因为乘积等于 n 只可能是 n 的约数，因此我们可以先预处理出所有的约数，最后 n 3 n^3 n3 枚举即可（只有128个约数）

#include <iostream>
#include <vector>

using namespace std;

typedef long long LL;

LL n;

int main()
{
    n=2021041820210418;
    vector<LL> a;

    for(LL i=1;i*i<=n;i++)
    {
        if(n%i==0)
        {
            a.push_back(i);
            a.push_back(n/i);
        }
    }

    int res=0;
    for(auto i:a)
        for(auto j:a)
            for(auto k:a)
                if(i*j*k==n) res++;

    cout<<res<<endl;

    return 0;
}

算法2： 直接暴力法（也就4s而已）

#include <iostream>

using namespace std;

typedef long long LL;

LL n;

int main()
{
    n=2021041820210418;

    int res=0;
    for(LL i=1;i*i*i<=n;i++)
        if(n%i==0)
            for(LL j=i;i*j*j<=n;j++) //j=i开始，保持递增
                if(n/i%j==0)
                {
                    LL k=n/i/j;
                    if(i==j&&i==k) res++;
                    else if(i==j||i==k||j==k) res+=3;
                    else res+=6;
                }

    cout<<res<<endl;

    return 0;
}

算法3： 筛质因子+手算排列组合比较快，也可以 dfs，但是要处理一下重复

筛质因子代码就不展示了
质因子及个数如下：
5882353 1
2857 1
131 1
2 1
17 1
3 3

D：路径

在这里插入图片描述
题解
知识点：最短路，dijkstra

  • 最短路问题，涉及到求最小公倍数 l c m ( a , b ) = a ∗ b / g c d ( a , b ) lcm(a,b)=a*b/gcd(a,b) lcm(a,b)=a∗b/gcd(a,b)
  • 听一些大佬说dp也可以，但是不清楚正确性，即是否一定从前往后走。
  • 由于本题数据范围很小加上是填空题，直接最暴力的 O ( n 2 ) O(n^2) O(n2) 迪杰即可。如果边过多或者 n 2 n^2 n2 超时可以考虑堆优化迪杰

答案：10266837

#include <iostream>
#include <cstring>

using namespace std;

const int N=2050;

int g[N][N],n;
bool st[N];
int dis[N];

int gcd(int a,int b)
{
    return b?gcd(b,a%b):a;
}

void djs()
{
    memset(dis,0x3f,sizeof dis);
    dis[1]=0;
    for(int k=0;k<n;k++)
    {
        int u=0;
        for(int i=1;i<=n;i++)
        {
            if(!st[i]&&dis[i]<dis[u]) u=i;
        }
        st[u]=true;
        if(u==2021) break;
        for(int i=1;i<=n;i++) dis[i]=min(dis[i],dis[u]+g[u][i]);
    }
}

int main()
{
    n=2021;
    for(int i=1;i<N;i++)
        for(int j=i;j<N;j++)
        {
            if(j-i>21) g[i][j]=g[j][i]=0x3f3f3f3f;
            else g[i][j]=g[j][i]=i*j/gcd(i,j);
        }

    djs();

    cout<<dis[n]<<endl;

    return 0;
}

E：回路计数

在这里插入图片描述
题解

  • 直接爆搜时间复杂度是阶乘级别的，即 O ( n ! ) O(n!) O(n!)，大概只能搜到15就不行了，原因在于每个点搜索顺序可以不一样，近似看成 n 的全排列就是阶乘级别了。
  • 仔细分析题目会发现每个点的状态我们都要处理到位，且要经过每个点，20是非常nice的一个数字，会想到什么：状态压缩，我们不妨用 ( 1 < < 21 ) − 1 (1<<21)-1 (1<<21)−1内的每个数字来表示所有状态，但是会发现如果只这样是不好处理的，因此再加入一维。
  • 状态表示： d p [ s t a t e ] [ j ] dp[state][j] dp[state][j] 表示当前经过了的点状态为 s t a t e state state 且最后一次经过的点为 j j j 的方案数。
  • 状态转移： d p [ s t a t e ] [ j ] = ∑ i = 0 20 d p [ s t a t e − 2 i ] [ k ] dp[state][j]= \sum_{i=0}^{20}dp[state-2^i][k] dp[state][j]=∑i=020​dp[state−2i][k]
    转移条件： s t a t e state state 的第 j j j 位是 1 并且 s t a t e state state 的第 k k k 位也是 1， j ! = k j!=k j!=k， g c d ( i + 1 , k + 1 ) = = 1 gcd(i+1,k+1)==1 gcd(i+1,k+1)==1。
  • 结果表示： r e s = ∑ i = 0 20 d p [ ( 1 < < 21 ) − 1 ] [ i ] res=\sum_{i=0}^{20}dp[(1<<21)-1][i] res=∑i=020​dp[(1<<21)−1][i]。有的小伙伴可能会问原因： d p [ ( 1 < < 21 ) − 1 ] [ i ] dp[(1<<21)-1][i] dp[(1<<21)−1][i]表示的是经过了所有点且最后在第 i i i 个位置上的方案数，现在并没有回到源点，也就是说最后的所有结尾点为 i i i 的方案中就是最后倒数第2个点，再往前走一步就是终点（原点）了，而最后的状态是由所有倒数第2的状态转移过来，所以将所有 d p [ ( 1 < < 21 ) − 1 ] [ i ] dp[(1<<21)-1][i] dp[(1<<21)−1][i]加起来就是最终回到原点的方案数，也就是哈密顿回路的方案数。

答案：881012367360

#include <bits/stdc++.h>
#define rep(i, l, r) for (int i = l; i <= r; i++)

using namespace std;

const int INF=0x3f3f3f3f,MOD=1000000007,P=131,N=22,M=400010;

int n=21;
long long dp[1<<21][21];
bool g[N][N];

int gcd(int a,int b)
{
    return b?gcd(b,a%b):a;
}

int main()
{
    rep(i,1,n)
        rep(j,i+1,n)
            if(gcd(i,j)==1) g[i][j]=g[j][i]=true;

    dp[1][0]=1;
    rep(i,2,1<<n)
        rep(j,0,20)
            if(i>>j&1)
                rep(k,0,20)
                    if(j!=k&&g[j+1][k+1]&&(i>>k&1))
                        dp[i][j]+=dp[i-(1<<j)][k];

    long long res=0;
    rep(i,0,20) res+=dp[(1<<21)-1][i];

    cout<<res<<endl;

    return 0;
}

F：砝码称重

在这里插入图片描述
在这里插入图片描述
题解
dp 可以做，枚举每一个砝码，再枚举所有已经存在的重量，加减当前重量a[i]即可，复杂度 O ( n m ) O(nm) O(nm)
状态方程：t[j]=t[j-a[i]]=true,t[j+a[i]]=true; 用前面轮的结果标记这一轮。
众所周知：一维肯定快点（滚动数组）
一维：

#include <iostream>
#include <cstring>

using namespace std;

const int N=110,M=200010,B=M/2;

int a[N],n;
bool f[M],t[M];

int main()
{
    cin>>n;
    int m=0;
    for(int i=1;i<=n;i++) cin>>a[i],m+=a[i];
    
    f[B]=1;
    for(int i=1;i<=n;i++)
    {
        for(int j=-m;j<=m;j++)
            if(f[j+B]) 
            {
                t[j+B]=true;
                t[j+a[i]+B]=t[j-a[i]+B]=true;
            }
        memcpy(f,t,sizeof t);
    }
    
    int res=0;
    for(int i=1;i<=m;i++) res+=f[i+B];
    cout<<res<<endl;
    
    return 0;
}

二维：

#include <iostream>

using namespace std;

const int N=110,M=200010,B=M/2;

bool f[N][M];
int a[N],n;

int main()
{
    cin>>n;
    int m=0;
    for(int i=1;i<=n;i++) cin>>a[i],m+=a[i];

    f[0][B]=1;
    for(int i=1;i<=n;i++)
    {
        for(int j=-m;j<=m;j++)
        {
            if(f[i-1][j+B]) f[i][j+B]=true; //不选
            if(f[i-1][j+B])
                f[i][j+a[i]+B]=f[i][j-a[i]+B]=true;
        }
    }

    int res=0;
    for(int i=1;i<=m;i++) res+=f[n][i+B];
    cout<<res<<endl;

    return 0;
}

G：异或数列

在这里插入图片描述
在这里插入图片描述
题解
知识点：博弈论
首先这类题咱们自己可以比划比划，可以找到一些性质

  • 如果所有数的异或和为 0，那么所有位的值都为偶数，每个数不管怎么选，双方的数最终都会相等，必然是平局
  • 不是平局，必然异或和有一个1，我们找到最高位的1，统计数列中这位为1的数量 c n t 1 cnt1 cnt1，它必定是奇数。如果如果Alice(先手)想赢，必然要使最高位掌握在自己手中，这里还有一个点就是这一位为0的元素数量 c n t 0 cnt0 cnt0，如果打不赢的时候，使用这一位为0的数可以使得攻防反转，最终我们要统计的就是 c n t 1 + c n t 0 cnt1+cnt0 cnt1+cnt0的数量，如果是奇数，则Alice必胜，反之Bob必胜
  • 值得注意的最后一点就是如果该异或值的最高位只有一位1，那么选了这个1后无论后面怎么选都是选了这个1的最大，因此如果 c n t 1 = 0 cnt1=0 cnt1=0，则 Alice 必胜，这个情况要先判。
#include <bits/stdc++.h>
#define x first
#define y second
#define all(x) x.begin(),x.end()
#define rep(i, l, r) for (int i = l; i <= r; i++)
#define nep(i, r, l) for (int i = r; i >= l; i--)
using namespace std;
typedef pair<int,int> PII;
typedef pair<pair<int,int>,int> PIII;
typedef long long LL;
typedef unsigned long long ULL;
const int INF=0x3f3f3f3f,MOD=1000000007,P=131,N=200010,M=200010;

int n;
int w[N];

int main()
{
    int T; cin>>T;
    while(T--)
    {
        scanf("%d",&n);

        int res=0;
        rep(i,1,n)
        {
            scanf("%d",&w[i]);
            res^=w[i];
        }
        if(res==0) puts("0");
        else
        {
            int k=30,cnt1=0,cnt0=0;
            while(!(res>>k&1)) k--;
            rep(i,1,n)
            {
                if(w[i]>>k&1) cnt1++;
                else cnt0++;
            }

            if(cnt1==1) puts("1");
            else if(n&1) puts("1");
            else puts("-1");
        }
    }

	return 0;
}

H：左孩子右兄弟

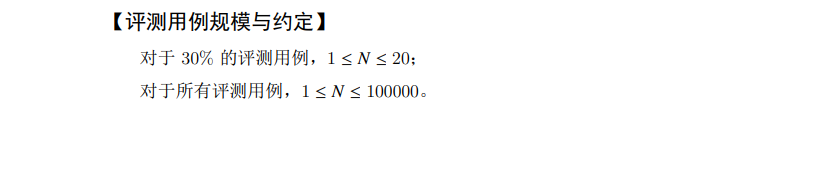
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
题解
知识点：树的遍历，树形DP
这题是给定一棵树，问怎么转可以使得树的深度最大

  • 首先孩子可以任意选，那么对于任意一个树上的结点，我们找到它的所有的子树中最深的一个孩子，然后统计它的孩子数量，把最深的这个孩子结点依次接到它所有孩子后面就可以了。例如：有三个子树，深度分别是 2，3，4，那么我们答案就是 4+1(接在2孩子上)+1(再接在3孩子上) = 6
#include <bits/stdc++.h>
#define x first
#define y second
#define all(x) x.begin(),x.end()
#define rep(i, l, r) for (int i = l; i <= r; i++)
#define nep(i, r, l) for (int i = r; i >= l; i--)
using namespace std;
typedef pair<int,int> PII;
typedef pair<pair<int,int>,int> PIII;
typedef long long LL;
typedef unsigned long long ULL;
const int INF=0x3f3f3f3f,MOD=1000000007,P=131,N=100010,M=200010;

int n;
int h[N],e[M],ne[M],idx;

void add(int a,int b)
{
    e[idx]=b,ne[idx]=h[a],h[a]=idx++;
}

int dfs(int u)
{
    int cnt=0,maxv=0;
    for(int i=h[u];~i;i=ne[i])
    {
        int j=e[i];
        cnt++;
        maxv=max(maxv,dfs(j));
    }

    return maxv+cnt;
}

int main()
{
    memset(h,-1,sizeof h);
    cin>>n;
    rep(i,2,n)
    {
        int x; scanf("%d",&x);
        add(x,i);
    }

    cout<<dfs(1)<<endl;

	return 0;
}

I：括号序列

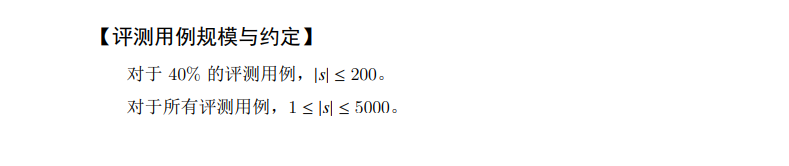
在这里插入图片描述
在这里插入图片描述
题解
这题才发现是个原题，可惜当时没写出来

  • 分别计算插左右括号的方案数
  • 计算另一种括号数的时候直接翻转再翻转符号就行了
  • 最后计算总方案数，其实就是插空法，分别插左右括号，最后相乘即可

DP分析：
状态表示： f [ i ] [ j ] f[i][j] f[i][j]：只考虑前i个括号并且左括号比右括号多 j j j 的方案数
状态转移：
当 s [ i ] = s[i]= s[i]=‘(’ ， f [ i ] [ j ] = f [ i − 1 ] [ j − 1 ] f[i][j]=f[i-1][j-1] f[i][j]=f[i−1][j−1];
反之 f [ i ] [ j ] = f [ i − 1 ] [ j + 1 ] + f [ i ] [ j − 1 ] f[i][j]=f[i-1][j+1]+f[i][j-1] f[i][j]=f[i−1][j+1]+f[i][j−1];（推导过程与完全背包类似）

  • 这里有个小问题就是有可能最终的答案刚好取模后 =0 造成返回值错误，但是这种情况十分罕见，可以忽略不计，也可以在官网通过，如果要避免这种情况可以参考代码2，通过计算最少需要添加的括号数 c n t cnt cnt，然后再计算出答案是需要返回几
#include <iostream>
#include <algorithm>
#include <cstring>

using namespace std;

typedef long long LL;

const int N=5010,MOD=1e9+7;

LL f[N][N];
int n;
char s[N];

LL get()
{
    memset(f,0,sizeof f);
    f[0][0]=1;
    for(int i=1;i<=n;i++)
    {
        if(s[i]=='(')
        {
            for(int j=1;j<=n;j++)
                f[i][j]=f[i-1][j-1];
        }
        else
        {
            f[i][0]=(f[i-1][1]+f[i-1][0])%MOD;
            for(int j=1;j<=n;j++)
                f[i][j]=(f[i-1][j+1]+f[i][j-1])%MOD;
        }
    }
    for(int i=0;i<=n;i++)
        if(f[n][i]) return f[n][i];
    return -1;
}

int main()
{
    scanf("%s",s+1);
    n=strlen(s+1);

    LL a=get();

    reverse(s+1,s+n+1);
    for(int i=1;i<=n;i++)
        if(s[i]=='(') s[i]=')';
        else s[i]='(';

    LL b=get();

    cout<<a*b%MOD<<endl;

    return 0;
}

代码2：

#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int INF=0x3f3f3f3f,MOD=1000000007,P=131,N=5010,M=2*N;

char s[N]; 
int n;
LL f[N][N];

LL calc()
{
	int cnt=0, k=0, l=0, r=0;
	for(int i=1;i<=n;i++)
	{
		if(s[i]==')') 
		{
			r++, k++;
			if(k>0) k=0,cnt++;
		}
		else l++,k--;
	}
	
	memset(f,0,sizeof f);
	f[0][0]=1;
	for(int i=1;i<=n;i++)
	{
		if(s[i]=='(') 
		{
			for(int j=1;j<=n;j++)
				f[i][j]=f[i-1][j-1];
		}
		else
		{
			f[i][0]=(f[i-1][1]+f[i-1][0])%MOD;
			for(int j=1;j<=n;j++)
				f[i][j]=(f[i-1][j+1]+f[i][j-1])%MOD;
		}
	}
	
	return f[n][cnt+l-r]; //直接返回答案
}

int main()
{
	scanf("%s",s+1);
	n=strlen(s+1);
	
	LL l=calc();
	reverse(s+1,s+n+1);
	for(int i=1;i<=n;i++) 
		if(s[i]==')') s[i]='(';
		else s[i]=')';
		
	LL r=calc();
	cout<<l*r%MOD<<endl;
	
	return 0;
}

J：分果果（题目）

在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

后续待官网题更新后再更新…心态爆炸

妍来那样美好
关注
  • 11
    点赞
  • 踩
  • 52
    收藏
    觉得还不错? 一键收藏
  • 5
    评论
专栏目录
第12届蓝桥杯大赛软件赛C++B组，省赛和国赛试题
12-19
无积分
（蓝桥真题）分果果（动态规划）
AC__dream的博客
03-09 2246
（蓝桥真题）分果果（动态规划）
蓝桥杯-回路计数
laosong_的博客
03-22 167
回路计数，蓝桥杯填空题
十三届蓝桥杯c/c++B组试题
06-30
十三届蓝桥杯c/c++B组试题试题 C: 卡牌试题 A: 2022试题 B: 钟表试题 D: 最大数字试题 E: 出差试题 F: 费用报销试题 G: 故障试题 H: 机房试题 I: 齿轮试题 I: 齿轮他一共有 n 块砖，他发现第 i 砖的重量为 wi，价值为 vi。他突然想从这些砖中选一些出来从下到上堆成一座塔，并且对于塔中的每一块砖来说，它上面所有砖的重量和不能超过它自身的价值。他想知道这样堆成的塔的总价值（即塔中所有砖块的价值和）最大是多少。他一共有 n 个齿轮，第 i 个齿轮的半径为 ri，他需要把这 n 个齿轮按一定顺序从左到右组装起来，这样最左边的齿轮转起来之后，可以传递到最右边的齿轮，并且这些齿轮能够起到提升或者降低转速 (角速度) 的作用他发现机房里一共有 n 台电脑，编号为 1 到 n，电脑和电脑之间有网线连 接，一共有 n − 1 根网线将 n 台电脑连接起来使得任意两台电脑都直接或者间 接地相连。 小明发现每台电脑转发、发送或者接受信息需要的时间取决于这台电脑和 多少台电脑直接相连, 而信息在网线中的传播时间可以忽略。比如如果某台电脑 用网线直接连接了另外 d 台
中班绘本教案《小老鼠分果果》.docx
01-07
中班绘本教案《小老鼠分果果》
2021年第十二届蓝桥杯决赛 C++大学A组 真题.zip
06-05
2021年第十二届蓝桥杯决赛C++大学A组 试题（2021.6.5） 比赛时间：2021.6.5
2021年第十二届蓝桥杯省赛A组题解（C/C++）
热门推荐
薛崇祥的博客
12-11 2万+
2021年第十二届蓝桥杯省赛A组C/C++语言组题解
2021年第十二届蓝桥杯大赛软件赛决赛C/C++大学A组 个人部分题解
nefu_ljw的博客
06-05 5763
这次国赛，基本上大题都是暴力写的，填空题只写了前两个，老混子选手了 不一定是正确题解，欢迎大家讨论交流解法，批评指正~ 文章目录 A题 纯质数（5分） B题 完全日期（5分） C题 最小权值（10分） D题 覆盖（10分） E题 123（15分） F题 异或变换（15分） G题 冰山（20分） H题 翻转括号序列（20分） I题 异或三角（25分） J题 积木（25分）
第十二届蓝桥杯 括号序列 dp
weixin_51182010的博客
04-05 419
不是特别理解，譬如（）时答案是1但是过评测机是没问题的。 可能给出的数据都是至少需要添加一个。 代码是照猫画虎写了一份，似懂非懂。 首先（）等价，不可能让你加一个（）这种匹配的，所以答案是两者乘积 处理一个，另一个倒转再相同处理即可 先处理加（的情况 dp[i][j]表示第i个字符（比)多j个的添加方法数 转移方程： 当前为（：f[i][j]=f[i-1][j-1]这时我们不加（因为加在哪都一样所以我们统一加载）左侧 当前为）：f[i][j]=(f[i-1][j+1]+f[i][j-1])%mod f[.
2023蓝桥杯大学A组C++国赛游记+个人题解
cqbzcsq的博客
06-10 1932
总之就是非常菜，简单题背不到公式，板题背不到板子，题目都写不完，太菜了。
12届蓝桥杯省赛c++b组 J题 括号序列
qq_51972900的博客
05-05 2万+
这次要讲的前几个星期刚比完的蓝桥杯c++b组的J题：括号序列。本次比赛我也参加了，但是这道题我是dfs求解的，所以都只是拿了少部分的分，我比赛时的代码就不展示了，因为时间复杂度很高，所以我就直接讲解正解应该怎么写了。 先上题目： 给定一个括号序列，要求尽可能少地添加若干括号使得括号序列变得合法，当添加完成后，会产生不同的添加结果，请问有多少种本质不同的添加结果。 两个结果是本质不同的是指存在某个位置一个结果是左括号，而另一个是右括号。 例如，对于括号序列 ((()，只需要添加两个括号就能让其合法，有以下几种
2021年第十二届蓝桥杯省赛大学A组题解C/C++代码
12-14
2021年第十二届蓝桥杯省赛大学A组题解C/C++代码
第十三届蓝桥杯大赛软件赛决赛_JG java 研究生组
06-20
第十三届蓝桥杯大赛软件赛决赛_JG java 研究生组
2022年第十三届蓝桥杯大赛软件赛C/C++ 大学 B 组省赛、省赛第二场、决赛
06-21
2022年第十三届蓝桥杯大赛软件赛C/C++ 大学 B 组省赛、省赛第二场、决赛
2019年蓝桥杯省赛第十届蓝桥杯真题C/C++(A组)
12-18
2019年4月1日蓝桥杯省赛第十届蓝桥杯真题C/C++(A组)!
第十二届蓝桥杯青少年组省赛C++.docx
04-14
第十二届蓝桥杯青少年组省赛C++真题，不包含答案，
第十五届蓝桥杯大赛软件赛省赛第二场 C/C++ 大学 A组
最新发布
04-22
第十五届蓝桥杯大赛软件赛省赛第二场 C/C++ 大学 a 组
第十五届蓝桥杯大赛软件赛省赛第二场C/C++ 大学A B C组试题
04-22
第十五届蓝桥杯大赛软件赛省赛第二场C/C++ 大学A B C组试题 对于编程题目，要求选手给出的解答完全符合 GNU C/C++ 标准，不能使 用诸如绘图、Win32API、中断调用、硬件操作或与操作系统相关的 API。 代码中允许使用 ...
第十二届蓝桥杯省赛 C/C++大学B组 试题J：括号序列
qq_44309679的博客
07-18 288
第十二届蓝桥杯省赛 C/C++大学B组 试题J：括号序列
2021第十三届蓝桥杯校内模拟赛c/c++ b组
09-08
2021第十三届蓝桥杯校内模拟赛C/C++B组题目需要参赛者使用C/C++语言完成一系列编程题目。这些题目涵盖了计算机科学与技术的各个方面，包括数据结构、算法、操作系统、数据库等等。 在比赛中，参赛者需要根据每道...

“相关推荐”对你有帮助么？

  • 非常没帮助
  • 没帮助
  • 一般
  • 有帮助
  • 非常有帮助
提交
评论 5
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值