5_栈

栈

Stack 概念

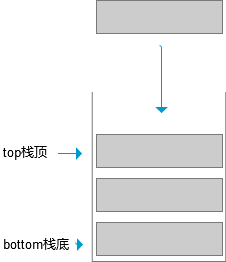
• 定义：栈是限定仅在表尾进行插入和删除操作的线性表
• 栈顶：允许插入和删除的一端
• 栈底：另外一端
• 特性：后进后出

• 图形：

  

进栈出栈的问题

• 有 1，2，3，4，5，五个整型数字，依次进栈，问出栈的次序有几种可能？34125 是合法的出栈顺序吗？

  • 第一个问题，C(2n, n)/(n+1)

    • 递归，折现法，卡特兰数：n个元素进栈，共有多少种出栈顺序？（转）

  • 第二个问题

    • 第一种解法：根据两个规则来判断

      • 规则一：最小的数，左边的数比右边的数小（由进栈数等于出栈数这个条件可以证明）

        • _ _ _ 1 _ 左边三个空位的数比右边一个空位的数小，即不可以出现类似于 _ 3 _ 1 2 这种情况
        • 判断完最小的数，再找第二小的数，做上面步骤的判断（即递归） _ 2 _ 1 5 ，2 左边空位的数比右边空位的数小，即只能是 3 2 4

      • 规则二：最大的数，后面是逆序排列的

        • _ _ 5 _ _ 即 5 右边只能是 4 3

    • 第二种解法：模拟进栈法（34215）

      • 依 1，2，3 顺序进栈，直到栈顶数与第一个数值相等，再出栈一次（3），并记录最大出栈数 maxFlag（3）
      • 若下一个数值 c（4） 大于 maxFlage（3），做与上一步类似的操作，即进栈、出栈一次（4）、记录 maxFlage
      • 若下一个数值 c（2） 小于 maxFlage（4），直接出栈一次（2），并判断出栈的值与 c 是否相等

      • 代码实现

        public boolean judge(String str){
            char maxFlag = '1';
            SqStack<Character> stack = new SqStack<>(9+26);
            char[] chars = str.toCharArray();
            stack.push('1');
            for (char c : chars){
                checkChar(c);
                if(c > maxFlag){
                    for(char i = ++maxFlag; i <= c; i++){
                        if(i > '9' && i < 'a')
                            i = 'a';
                        stack.push(i);
                    }
                    maxFlag = c;
                }
                char temp = stack.pop();
                if(temp != c)
                    throw new IllegalArgumentException("错误字符：" + c);
            }
            return true;
        }
        

• github源码链接

栈的顺序存储结构

• 用数组存储数据，将下标为 0 的一端作为栈底，另一端作为栈顶。因为栈顶插入删除频繁

• 定义 int top 作为栈顶，初始值为 -1

  • 代码实现

    public class SqStack<E> {
        private static final int MAXSIZE = 20;
        private int top = -1;
        private E data[];
    }
    

• 入栈操作

  • 将元素赋值给 data[top+1]，并 top++

  • 代码实现

    public boolean push(E element){
        if(this.top == MAXSIZE-1)
            throw new IndexOutOfBoundsException("栈已经达到最大存储空间："+MAXSIZE);
        this.data[++this.top] = element;
        return true;
    }
    

• 出栈操作

  • 将 data[top] 元素取出来并赋给 tempElement，清除 data[top]，top–

  • 代码实现

    public E pop(){
        if(this.top == -1)
            throw new IndexOutOfBoundsException("栈为空，不能再进行出栈操作");
        E topElement = this.data[this.top];
        this.data[this.top] = null;
        top--;
        return topElement;
    }
    

• 两栈共享空间

  • 图形

    

  • 说白了就是一个数组两个栈一起用，以达到合理利用空间的目的
    
    • 栈1 以下标 0 为栈底，栈2 以最后一个位置为栈底
    • 入栈时，向中间靠拢
    • 栈1，top1 == -1 为空栈；栈2，top2 == MAXSIZE 为空栈
    • top1 + 1 == top2 是为栈满
  • 这一部分没写代码
• github源码链接

栈的链式存储结构

• 用链表存储数据，将最后一个节点做为栈顶，第一个节点做为栈底。（反过来也一样）

• 图形，虚线为入栈操作：

  

• 由于将最后一个节点做为栈顶，pop 操作时需要获取前一个节点，故定义双向链表

  • 代码实现

    public class LinkStack<E> {
        private Node<E> top;
        private Node<E> firstNode;
        private int count=0;
    
        class Node<E> {
            private E data;
            private Node next;
            private Node pre;
        }
    }
    

• 入栈操作

  • 将元素给到 newNode，top 下个节点指向 newNode，最后 top 移动到下一个节点

  • 代码实现

    public int push(E element){
        if(this.firstNode == null){
            this.firstNode = new Node(element);
            this.top = this.firstNode;
            return ++count;
        }
        Node newNode = new Node(element, top);
        top.next = newNode;
        top = top.next;
        return ++count;
    }
    

• 出栈操作

  • 将 top 赋给 tempNode，获取 tempNode 的值给 element，top 移动到 tempNode 上一个节点（即原来 top 节点的上一个），清除 top.next，返回 element

  • 代码实现

    public E pop(){
        if(this.firstNode == null)
            throw new IndexOutOfBoundsException("栈已经没有元素，不能执行出栈操作");
        if(this.firstNode == this.top){
            E element = firstNode.data;
            firstNode = null;
            top = null;
            this.count--;
            return element;
        }
        Node<E> tempNode = top;
        E element = tempNode.data;
        top = tempNode.pre;
        top.next = null;
        this.count--;
        return element;
    }
    

• github源码链接