一、基本信息
标题:Distinctive Image Features from Scale-Invariant Keypoints
时间:2004
出版源:International Journal of Computer Vision
论文领域:计算机视觉.特征提取
引用格式:Lowe, D.G. Distinctive Image Features from Scale-Invariant Keypoints. International Journal of Computer Vision 60, 91–110 (2004).
链接:https://doi.org/10.1023/B:VISI.0000029664.99615.94
二、研究背景
Harris角探测器对图像尺度的变化非常敏感。因此,对于不同尺度的图像匹配,Harris的角反射器并不能提供很好的基础。
还没有一个方法实现了完全的仿射不变性
三、创新点
尺度不变性

高斯金字塔
图像的尺度空间表示
L
(
x
,
y
,
σ
)
=
G
(
x
,
y
,
σ
)
∗
I
(
x
,
y
)
L(x, y, \sigma)=G(x, y, \sigma)^{*} I(x, y)
L(x,y,σ)=G(x,y,σ)∗I(x,y)
G ( x , y , σ ) = 1 2 π σ 2 e − ( x 2 + y 2 ) / 2 σ 2 G(x, y, \sigma)=\frac{1}{2 \pi \sigma^{2}} e^{-\left(x^{2}+y^{2}\right) / 2 \sigma^{2}} G(x,y,σ)=2πσ21e−(x2+y2)/2σ2
G ( x , y , σ ) = 1 2 π σ 2 e − ( x − m / 2 ) 2 + ( y − n / 2 ) 2 2 σ 2 G(x, y, \sigma)=\frac{1}{2 \pi \sigma^{2}} e^{-\frac{(x-m / 2)^{2}+(y-n / 2)^{2}}{2 \sigma^{2}}} G(x,y,σ)=2πσ21e−2σ2(x−m/2)2+(y−n/2)2
m,n表示高斯模板的维度(由 ( 6 σ + 1 ) × ( 6 σ + 1 ) (6 \sigma+1) \times(6 \sigma+1) (6σ+1)×(6σ+1)确定)。(x, y)代表图像的像素位置。是尺度空间因子,值越小表示图像被平滑的越少,相应的尺度也就越小。大尺度对应于图像的概貌特征,小尺度对应于图像的细节特征。

为了让尺度体现其连续性,高斯金字塔在简单降采样的基础上加上了高斯滤波。将图像金字塔每层的一张图像使用不同参数做高斯模糊,使得金字塔的每层含有多张高斯模糊图像,将金字塔每层多张图像合称为一组(Octave),金字塔每层只有一组图像,组数和金字塔层数相等,每组含有多张(也叫层Interval)图像。另外,降采样时,高斯金字塔上一组图像的初始图像(底层图像)是由前一组图像的倒数第三张图像隔点采样得到的。
高斯差分金字塔
2002年Mikolajczyk在详细的实验比较中发现尺度归一化的高斯拉普拉斯函数 σ 2 ∇ 2 G \sigma^{2} \nabla^{2} G σ2∇2G的极大值和极小值同其它的特征提取函数,例如:梯度,Hessian或Harris角特征比较,能够产生最稳定的图像特征。
D ( x , y , σ ) = [ G ( x , y , k σ ) − G ( x , y , σ ) ] ∗ I ( x , y ) = L ( x , y , k σ ) − L ( x , y , σ ) \begin{aligned} D(x, y, \sigma) &=[G(x, y, k \sigma)-G(x, y, \sigma)] * I(x, y) \\ &=L(x, y, k \sigma)-L(x, y, \sigma) \end{aligned} D(x,y,σ)=[G(x,y,kσ)−G(x,y,σ)]∗I(x,y)=L(x,y,kσ)−L(x,y,σ)
而Lindeberg早在1994年就发现高斯差分函数(Difference of Gaussian ,简称DOG算子)与尺度归一化的高斯拉普拉斯函数 σ 2 ∇ 2 G \sigma^{2} \nabla^{2} G σ2∇2G非常近似。
在实际计算时,使用高斯金字塔每组中相邻上下两层图像相减,得到高斯差分图像,进行极值检测。高斯差分算子更高效。
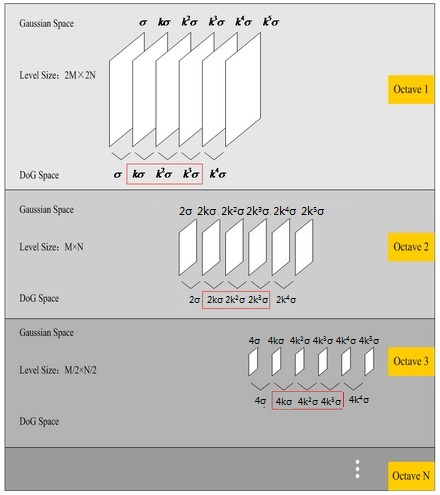
空间极值点检测(关键点的初步探查)

中间的检测点和它同尺度的8个相邻点和上下相邻尺度对应的9×2+8个点共26个点比较,以确保在尺度空间和二维图像空间都检测到极值点。
关键点的精确定位
候选特征点x, 其偏移量定义为
Δ
x
,
\Delta x,
Δx, 其对比度为
D
(
x
)
D(x)
D(x) 的绝对值
∣
D
(
x
)
∣
,
|D(x)|,
∣D(x)∣, 对
D
(
x
)
D(x)
D(x) 应用泰勒展开式
D
(
x
)
=
D
+
∂
D
T
∂
x
Δ
x
+
1
2
Δ
x
T
∂
2
D
∂
x
2
Δ
x
D(x)=D+\frac{\partial D^{T}}{\partial x} \Delta x+\frac{1}{2} \Delta x^{T} \frac{\partial^{2} D}{\partial x^{2}} \Delta x
D(x)=D+∂x∂DTΔx+21ΔxT∂x2∂2DΔx
由于x是D(x)的极值点, 所以对上式求导并令其为0, 得到
Δ
x
=
−
∂
2
D
−
1
∂
x
2
∂
D
(
x
)
∂
x
\Delta x=-\frac{\partial^{2} D^{-1}}{\partial x^{2}} \frac{\partial D(x)}{\partial x}
Δx=−∂x2∂2D−1∂x∂D(x)
然后再把求得的
Δ
x
\Delta x
Δx 代入到D(x)的泰勒展开式中
D
(
x
^
)
=
D
+
1
2
∂
D
T
∂
x
x
^
D(\hat{x})=D+\frac{1}{2} \frac{\partial D^{T}}{\partial x} \hat{x}
D(x^)=D+21∂x∂DTx^
若|
D
(
x
^
)
∣
≥
T
,
D(\hat{x}) | \geq T,
D(x^)∣≥T, 则该特征点保留, 否则易除掉。对于本文中的实验来说,
T
=
0.03
T=0.03
T=0.03
消除边缘响应
在边缘梯度的方向上主曲率值比较大, 而沿着边绿方向则主曲率值较小。候选特征点的DoG函数D(x)的主曲率与2 * 2Hessian矩阵H的特征值成正2
H
=
[
D
x
x
D
y
x
D
x
y
D
y
y
]
H=\left[\begin{array}{ll} D_{x x} & D_{y x} \\ D_{x y} & D_{y y} \end{array}\right]
H=[DxxDxyDyxDyy]
其中,
D
x
x
,
D
x
y
,
D
y
y
D_{x x}, D_{x y}, D_{y y}
Dxx,Dxy,Dyy 是候选点邻域对应位置的差分求得的。 为了避免求具体的值, 可以使用H特征值得比例。设
α
=
λ
m
a
x
\alpha=\lambda_{m a x}
α=λmax 为H的最大特征值,
β
=
λ
m
i
n
\beta=\lambda_{m i n}
β=λmin 为旧最小特征值,则
Tr
(
H
)
=
D
x
x
+
D
y
y
=
α
+
β
Det
(
H
)
=
D
x
x
+
D
y
y
−
D
x
y
2
=
α
⋅
β
\begin{array}{c} \operatorname{Tr}(H)=D_{x x}+D_{y y}=\alpha+\beta \\ \operatorname{Det}(H)=D_{x x}+D_{y y}-D_{x y}^{2}=\alpha \cdot \beta \end{array}
Tr(H)=Dxx+Dyy=α+βDet(H)=Dxx+Dyy−Dxy2=α⋅β
其中,Tr
(
H
)
(H)
(H) 为矩阵H的迹,
Det
(
H
)
\operatorname{Det}(H)
Det(H) 为矩阵H的行列式。 设
γ
=
α
β
\gamma=\frac{\alpha}{\beta}
γ=βα 表示最大特征值和最小特征值的比值, 则
Tr
(
H
)
2
Det
(
H
)
=
(
α
+
β
)
2
α
β
=
(
γ
β
+
β
)
2
γ
β
2
=
(
γ
+
1
)
2
γ
\frac{\operatorname{Tr}(H)^{2}}{\operatorname{Det}(H)}=\frac{(\alpha+\beta)^{2}}{\alpha \beta}=\frac{(\gamma \beta+\beta)^{2}}{\gamma \beta^{2}}=\frac{(\gamma+1)^{2}}{\gamma}
Det(H)Tr(H)2=αβ(α+β)2=γβ2(γβ+β)2=γ(γ+1)2
上式的结果与两个特征值的比例有关, 和具体的大小无关, 当两个特征值想等时其值最小,并且随着
γ
\gamma
γ的增大而增大。因此为了检测主曲率是否在某个阅值
T
γ
T_{\gamma}
Tγ 下, 只需检通,
Tr
(
H
)
2
Det
(
H
)
>
(
T
γ
+
1
)
2
T
γ
\frac{\operatorname{Tr}(H)^{2}}{\operatorname{Det}(H)}>\frac{\left(T_{\gamma}+1\right)^{2}}{T_{\gamma}}
Det(H)Tr(H)2>Tγ(Tγ+1)2
如果上式成立, 则易除该特征点, 否则保留。(本论文中取
T
γ
=
10
)
\left.T_{\gamma}=10\right)
Tγ=10)
旋转不变性
找到了特征点,也就可以得到该特征点的尺度σ,也就可以得到特征点所在的尺度图像
L
(
x
,
y
)
=
G
(
x
,
y
,
σ
)
∗
I
(
x
,
y
)
L(x, y)=G(x, y, \sigma) * I(x, y)
L(x,y)=G(x,y,σ)∗I(x,y)
每个点L(x,y)的梯度的模m(x,y)以及方向θ(x,y)可通过下面公司求得
m
(
x
,
y
)
=
[
L
(
x
+
1
,
y
)
−
L
(
x
−
1
,
y
)
]
2
+
[
L
(
x
,
y
+
1
)
−
L
(
x
,
y
−
1
)
]
2
m(x, y)=\sqrt{[L(x+1, y)-L(x-1, y)]^{2}+[L(x, y+1)-L(x, y-1)]^{2}}
m(x,y)=[L(x+1,y)−L(x−1,y)]2+[L(x,y+1)−L(x,y−1)]2
θ
(
x
,
y
)
=
arctan
L
(
x
,
y
+
1
)
−
L
(
x
,
y
−
1
)
L
(
x
+
1
,
y
)
−
L
(
x
−
1
,
y
)
\theta(x, y)=\arctan \frac{L(x, y+1)-L(x, y-1)}{L(x+1, y)-L(x-1, y)}
θ(x,y)=arctanL(x+1,y)−L(x−1,y)L(x,y+1)−L(x,y−1)
得到特征点的主方向后,对于每个特征点可以得到三个信息 ( x , y , σ , θ ) (x,y,σ,θ) (x,y,σ,θ),即位置、尺度和方向。由此可以确定一个SIFT特征区域,一个SIFT特征区域由三个值表示,中心表示特征点位置,半径表示关键点的尺度,箭头表示主方向。具有多个方向的关键点可以被复制成多份,然后将方向值分别赋给复制后的特征点,一个特征点就产生了多个坐标、尺度相等,但是方向不同的特征点
关键点描述
中央为当前关键点的位置,每个小格代表为关键点邻域所在尺度空间的一个像素,求取每个像素的梯度幅值与梯度方向,箭头方向代表该像素的梯度方向,长度代表梯度幅值,然后利用高斯窗口对其进行加权运算。

为了增强匹配的稳健性,Lowe建议对每个关键点使用4×4共16个种子点来描述,这样一个关键点就可以产生128维的SIFT特征向量。

四、实验结果

五、结论与思考
作者结论
本文中所述的SIFT关键点对图像旋转具有不变性,对大尺度的仿射变形具有鲁棒性。从典型图像中可以提取大量的关键点,从而使在混杂背景下提取小目标具有更好的鲁棒性。可以从整个尺度范围提取关键点意味着小的局部特征可以与小而高度遮挡的目标进行匹配,而大的关键点则在图像噪音和模糊时具有了更好的表现。
本文还提出了一种用关键点进行目标识别的方法。这种方法使用了近似的近邻查找,用来识别与目标姿态一致的聚类的Hough变换和最小二乘法进行最后的决策和核查。另一个可能的应用是三维重建、运动跟踪和分割、机器人定位、图像全景集合(assembly)、对极(epipolar)配准和其他需要进行图像间匹配位置识别的视角匹配。
总结
DoG尺度空间的极值检测。 首先是构造DoG尺度空间,在SIFT中使用不同参数的高斯模糊来表示不同的尺度空间。而构造尺度空间是为了检测在不同尺度下都存在的特征点,特征点的检测比较常用的方法是Δ2G(高斯拉普拉斯LoG),但是LoG的运算量是比较大的,Marr和Hidreth曾指出,可以使用DoG(差分高斯)来近似计算LoG,所以在DoG的尺度空间下检测极值点。
删除不稳定的极值点 主要删除两类:低对比度的极值点以及不稳定的边缘响应点。
确定特征点的主方向 以特征点的为中心、以3×1.5σ为半径的领域内计算各个像素点的梯度的幅角和幅值,然后使用直方图对梯度的幅角进行统计。直方图的横轴是梯度的方向,纵轴为梯度方向对应梯度幅值的累加值,直方图中最高峰所对应的方向即为特征点的方向。
生成特征点的描述子 首先将坐标轴旋转为特征点的方向,以特征点为中心的16×16的窗口的像素的梯度幅值和方向,将窗口内的像素分成16块,每块是其像素内8个方向的直方图统计,共可形成128维的特征向量。
思考
特征点128维是表示一个DoG极值点?那么实际上一个特征点有n*s个128维组成。
SIFI算子最后的匹配,使用RANSAC算法与本文提出的Hough变换和最小二乘相比,效果怎么样?
























 314
314

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








