LLVM SSA 介绍

最近做研究碰到了一个难题，需要对程序变量按生命期进行重命名。考虑到 SSA 中一个变量在不同的程序分支中赋值时会进行重命名，因此打算以此作为参考，看看能否采取同样的方法达到目的。由于之前看到的文档中都说 LLVM IR 是 SSA 形式的，然而在用 Clang 打印生成 LLVM IR 后发现它并不是 SSA 形式，百思不得其解。本篇文章是查阅资料后对此问题的解答，顺便介绍了 LLVM SSA 的相关知识。

SSA 介绍

1 概念

首先看一下维基对静态单一赋值（SSA）形式的定义：

In compiler design, static single assignment form (often abbreviated as SSA form or simply SSA) is a property of an intermediate representation (IR), which requires that each variable is assigned exactly once, and every variable is defined before it is used.

– From Wikipedia

从上面的描述可以看出，SSA 形式的 IR 主要特征是每个变量只赋值一次。相比而言，非 SSA 形式的 IR 里一个变量可以赋值多次。为了得到 SSA 形式的 IR，起初的 IR 中的变量会被分割成不同的版本（version），每个定义（definition：静态分析术语，可以理解为赋值）对应着一个版本。在教科书中，通常会在旧的变量名后加上下标构成新的变量名，这也就是各个版本的名字。显然，在 SSA 形式中，UD 链（Use-Define Chain）是十分明确的。也就是说，变量的每一个使用（use：静态分析术语，可以理解为变量的读取）点只有唯一一个定义可以到达。

注释：关于 UD 链的详细解释，可以参考维基给出的说明 Use-define chain 。在这里我们只需要知道，编译器在做常量传播、公共子表达式删除等优化之前，必须获取程序的 UD 链和 DU 链。显然，UD 链越简洁，越方便做编译优化。

2 为什么要使用 SSA ？

SSA 通过简化程序中变量的特性，可以同时达到两种目的：第一，可以简化很多编译优化方法的过程；第二，对很多编译优化方法来说，可以获得更好的优化结果。下面给出一个例子：

 y := 1
 y := 2
 x := y

显然，我们一眼就可以看出，上述代码第一行的赋值行为是多余的，第三行使用的 y 值来自于第二行中的赋值。对于采用非 SSA 形式 IR 的编译器来说，它需要做数据流分析（具体来说是到达-定义分析）来确定选取哪一行的 y 值。但是对于 SSA 形式来说，就不存在这个问题了。如下所示：

 y1 := 1
 y2 := 2
 x1 := y2

显然，我们不需要做数据流分析就可以知道第三行中使用的 y 来自于第二行的定义，这个例子很好地说明了 SSA 的优势。除此之外，还有许多其他的优化算法在采用 SSA 形式之后优化效果得到了极大提高。甚至，有部分优化算法只能在 SSA 上做。

3 如何生成 SSA ？

把程序转换为 SSA 形式，最简单的方法就是将每个被赋值的变量用一个新的变量（版本）来取代，同时将每次使用的变量替换为这个变量到达该程序点的“版本”。以下面左边的流图为例，右边的流图则是按照这个方法生成的 SSA：

    

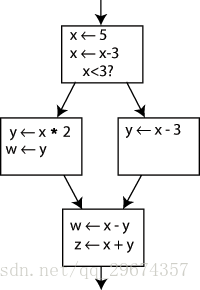
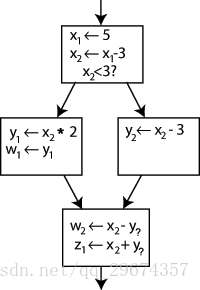
图一 原程序流图          图二 SSA 形式的程序

眼尖的人可以发现，右边的图其实也不是最后的 SSA 形式，它最下面的基本块里 y 的使用尚未确定。由于该基本块的多个前驱基本块里都对 y 进行了定义，这里我们并不知道程序最终会从哪个前驱基本块到达该基本块。那么，我们如何知道 y 该取哪个版本？这时候 Φ(Phi) 函数便出场了。

我们在最后一个基本块的起始处添加了一条新的语句（Φ），它给出了 y 的一个新的定义 y3，根据程序的运行路径选择对应的版本。最后得出的 SSA 如下图所示：

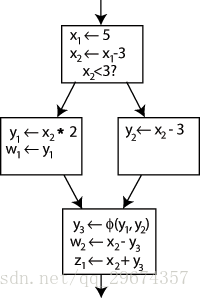
图三 最终的 SSA

要注意的是，Φ 函数并不是一条实际的指令，现在的 target 指令集大多都不支持这样的指令，因此需要编译器做特殊处理。编译器后端在碰到 Φ 函数时，会进行相关处理得到正确的汇编代码，这个过程叫做 resolution。知乎有一个帖子专门介绍了 Phi 的处理方式，可以戳这里：Phi Node 是如何实现它的功能的？

4 如何插入 Φ 函数 ？

根据上面的了解，我们可以知道实现 SSA 的一个关键点是 Φ 函数。自然而然的，我们需要回答下述问题：给出任意一个控制流图，在哪里插入 Φ 函数？哪些变量需要 Φ 函数来进行选择？这些问题很难，但是迄今已经有了一个高效的解决方案。该方法的计算涉及到我们下面要介绍的一个概念：支配边界。

4.1 求解支配边界

在介绍支配边界之前，简单回顾一下支配点（dominator）的概念，这个概念在另一篇博客上有介绍（控制流分析之循环）。在控制流图中，我们称结点 A 严格支配（strictly dominate）结点 B 当且仅当结点 A 与 B 并非同一结点，并且到达结点 B 的所有路径都包含结点 A。简单说，在到达结点 B 的时候，结点 A 中的代码都跑了一遍。要注意的是，概念严格支配和概念支配的区别在于俩结点是否同一节点。如果结点 A 与结点 B 可以是同一结点，那么称结点 A 支配（dominate）结点 B。换句话说，一个结点一定支配它本身。

现在可以提出支配边界（dominance frontiers）的概念了：如果结点 A 并不严格支配结点 B，而是支配结点 B 的立即前驱，那么结点 B 就在结点 A 的支配边界中。要特别注意以下情况，即当结点 A 不严格支配结点 B 且结点 A 就是结点 B 的立即前驱时，由于所有结点都支配它本身，于是结点 A 也支配它本身，这种情况下结点 B 也在结点 A 的支配边界里。从结点 A 的角度来看，可以把支配边界理解为结点 A 的支配关系终止的地方，也就是会有其他控制流出现的地方。

显然，通过支配边界可以准确获取到 Φ 函数应当出现的地方。如果结点 A 定义了某个变量，那么这个变量会到达被结点 A 支配的每一个结点。我们只有抛开这些结点，考虑支配边界，才会发现有其他的控制流可能对同样的变量进行了定义。下面介绍一个计算支配边界的主流算法，它是由 Cooper 等人在论文《A Simple, Fast Dominance Algorithm》中提出：

1 for each node b
2   if the number of immediate predecessors of b ≥ 2
3     for each p in immediate predecessors of b
4       runner := p
5       while runner ≠ idom(b)
6         add b to runner’s dominance frontier set
7         runner := idom(runner)

注意 1：上述算法中出现的 idom(b) 即立即支配（immediate dominate）结点 b 的结点。顾名思义，结点 b 的立即支配结点是指在支配树（dominator tree）中结点 b 的父亲，也就是离结点 b 最近的支配结点。对于非 entry 结点来说，这样的结点有且只有一个。

注意 2：对于只有一个立即前驱的结点来说，这个前驱也一定是它的立即支配结点。因此，上述算法第五行的循环条件恒不成立，没有必要考虑这种情况。

4.2 Φ 函数插入算法

在求出了支配边界后，后面的工作就简单很多了。接着，我们需要利用上一节求出的支配边界，求解需要使用 Φ 函数的基本块。下面给出一个插入算法的例子，该算法在所有支配边界的结点中插入了 Φ 函数：

// has-phi(