日撸 Java 三百行（特殊训练：关键路径）

日撸 Java 三百行（特殊训练：关键路径）

注意：这里是JAVA自学与了解的同步笔记与记录，如有问题欢迎指正说明

---

前言

今天是额外的练习日，所以我们直接跳过括号匹配来完成图中的关键路径这一章。
本章因为难度问题，我们直接略去相关的引入与介绍，直接开始关于理解代码与数据结构构造的过程，目的在于记录自己理解关键路径之余同时也保证被人能很好看懂。

一、关于AOE网 (Activity On Edge Network): 一个活动在边的有向无环图

在引入关键路径的概念之前，我们必须先了解AOE这种有向无环图的数据结构，在AOE网中，正如其名字——用边表示活动(Activity)的网络，每个边都拥有自己的权值（有权值的图叫做网），而这个权值代表的就是 一个活动(Activity)的持续时间，比如像：手洗袜子要5min，写完作业要1h等这样的“ 活动 ”。

而AOE中的每个 结点代表的是一个事件(Event) ，那么什么算事件呢，事件具有一种瞬时性，其不同于活动的持续性，事件往往是即可发生即可结束，比如我把衣服放到洗衣机里面洗，洗衣机花了30min来卷洗，这个是一个持续30min的活动(Activity)。然后30min到了，洗衣机发出洗好的提示音，你意识到洗衣完成了，这个瞬间就是一个事件(Event)——衣服洗好了。

事件可以是抽象的，时间含义可以比较模糊。比如我考上研了，或者我成年了，我中奖了，我要开始写作业了等这样的抽象的，时间感不持续的事件。从活动的角度来看，一个事件就像一个分水岭，它预示这个事件之前的活动的结束与之后活动的开始。

AOE的一些简单的性质与概念

AOE网具有下列这样的两个性质：

1. 只有在某顶点所代表的的事件发生，从该顶点出发的各有向边所代表的活动才能开始。
   

2. 只有在进入某顶点的各有向入边所代表的活动都已经结束，此结点所代表的的事件才能顺利发生。
   

综上可以发现，一个事件要想发生，必要要依靠最长的那个活动，因为最长的活动完成了，最短的活动也一定完成了，届时，所有活动都是呈现完成的状态。反之不然。

然后，我们来根据这个图来引入一些概念：
1). AOE网中仅有一个入度为0的顶点，称为开始顶点(源点)，它表示整个工程的开始。
2). AOE网中仅有一个出度为0的顶点，称为结束顶点(汇点)，它表示整个工程的结束。

而我们的AOE构造的工程规划中，我们最关心的问题无外乎有两个：
第一、完成整个工程最少要多久？
第二、哪些活动是影响我们工程进度的关键？

这些问题都可以总结为我们的关键路径问题，关键路径，我们定义：
从源点到汇点的所有路径中，具有最大路径长度的路径称之为关键路径。关键路径上的所有活动称之为关键活动

但是我们不是要求完成工程所需要最少的事件吗，为何我们选择最长的路径呢？
这其实涉及木桶效应，如我们刚才所说，只有在事件的入边活动全部都完成了，这个事件才能开始，而且入边活动全部宣告完成要取决于时间消耗最久的那个，例如早上8:30给6个人发布了任务，要求在全部人完成后才开集体会议，那么集体会议召开的时间肯定不取决于最快完成这个任务的人，而且取决于最慢完成这个任务的人。

于是，求工程完成的最少时间，就变为求关键路径的问题，或者更细致一点，求最长路径的问题。

二、一些关键的用于度量的数据结构

要求解关键路径的前提是需要对我们的问题进行抽象化，进行相应的问题建模。于是得到一下四个关键的度量：

1.关于事件结点的：最早发生时间

我们定义ve(v_j)表示事件v_j发生的最早时间。还是用我们刚刚图的部分来说明：

像这个图的一部分v₁因为是活动的最开始结点，因此，ve(v₁) = 0。即活动能在当前立马开始，无需等待。
我们假设事件单位是小时，v₂需要等待a₁历时的3h完成后才能开始，然后活动v₁从0时刻就开始了，因此ve(v₂) = 0 + 3 = 3。
ve(v₃)同理 = 0 + 2 = 2。
那么v₄要怎么考虑呢，很简单，通过我们刚刚说到的AOE网的第二性质：

只有在进入某顶点的各有向入边所代表的活动都已经结束，此结点所代表的的事件才能顺利发生

那么我们看看这些边什么时候完成，a₃的完成要经历0 + 3 + 2 = 5；a₅的完成要经历0 + 2+ 4 = 6。
所以v₄的两个入边分别在5h与6h后完成，若取某个时间点能让大家同时完成了，那么一定是6h而不是5h。

因此，你一定发现了，我们取的是权值最大的那个边，因此我们可以得到结点k的ve(v_k)转移方程：

ve(v_k) = Max{ ve(v_j) + Weight(v_j, v_k) }

这里的v_j是v_k的任意一个前驱节点，Weight(v_j, v_k)表示结点j与k之间的权值。
例如，就我们的图来说，活动a₅ = Weight(v₃, v₄) = 4

2.关于事件结点的：最迟发生时间

我们定义vl(v_j)表示事件v_j的最迟发生时间。还是用我们刚刚图的部分来说明：

我们结合生活时间想想，我们讨论一个事件的最迟什么发生，时向未来考虑还是向过去考虑？
假如我5月要复试，我现在准备专业课面试必须留1个月背概念，那么要最起码在4月初就要开始准备，不然就来不及了。
现在是上午，我晚上8:30有个会议，那么我最迟下午就要开始准备不然就来不及了。
可见最迟的时间度量我们是“ Based on future ”，而从过去出发。

所以我们进行假设，作为汇点的v₆，假设规定需要在27h完成v₆，那么现在v₄的最迟时间vl(v₄) = 27 - 2 = 25。同理：vl(v₅) = 27 - 1 = 26 。
那么v₃呢？它有v₄和v₆两个出边，v₄到v₃的最迟时间是25 - 4 =21，v₆到v₃的最迟时间是27 - 3 = 24。解释就是，若完成v₃后，v₄要留有足够去完成的话，v₃必须在21h时或之前做完；若完成v₃后，v₆要留有足够去完成的话，v₃必须在24h时或之前做完。

那么是你，你会在什么时候做完以保证v₄与v₆时间够用呢？
答案显而易见，选21h。21h要早于24h，选择21h时不仅v₄能卡住deadline完成，v₆也还有3h富裕的时间，但是若选择21h~24h的一个时间点，虽然v₆不会紧张，但是v₄已经延期了。大于24h更不可能了，两个都延期了。

可见这也是木桶原理，我们要保护最小的那个，那个是底线。可得结点k的vl(v_k)转移方程：

vl(v_k) = Min{ vk(v_j) - Weight(v_k, v_j) }

这里的v_j是v_k的任意一个后继节点，Weight(v_k, v_j)表示结点k与j之间的权值。
例如，就我们的图来说，活动a₆ = Weight(v₃, v₆) = 3

3.关于活动边的：最早开始时间

上述我们算出了任何一个事件（“点”）的最早开始时间与最迟开始时间度量，现在我们的视角从“ 点 ” 挪到“ 边 ”上来，也就是从事件的讨论转变为活动的讨论。

有了之前的讨论，我们假设每个点的ve(k)与vl(k)都是确定的了，这样关于边的讨论就变得容易多了。

我们定义e(a_j)表示活动a_j的最早发生时间。

活动a₄最早什么时候发生？
通过AOE的第一性质：

只有在某顶点所代表的的事件发生，从该顶点出发的各有向边所代表的活动才能开始。

可得，看a₄活动最早什么时候发生，必须看 最早什么时候v₂事件发生。
最早什么时候v₂事件发生…？这个问题为什么这么熟悉？这不是ve(v₂)的定义吗！
所以可以得到一个关键的结论：

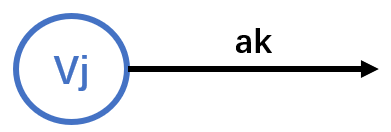
e(a_k) = ve(v_j)

这里活动点v_j是事件a_k的前驱节点：

4.关于活动边的：最迟开始时间

我们定义l(a_j)表示活动a_j的最迟发生时间。

活动a₄最迟什么时候发生？

与事件最迟发生的分析一致，我们还是尽可能向后看。我们已经知晓v₅的最迟发生事件vl(v₅)，而a₄是此事件唯一的前置边，或者说是触发这个事件发生的唯一活动，那么很自然，a₄的最迟发生时间应该vl(v₅) - a₄。
但是活动是独立，他不是顶点，他没有若干出边干扰他的取值，因此，活动本身与事件入边多少或出表多少没有任何关系，比如这里假如v₆最迟24h就要执行，那么a₈最迟只能从(24h - 1h = 25h)开始，a₇只能从(24h - 2h = 22h)开始

所以可以得到一个关键的结论：

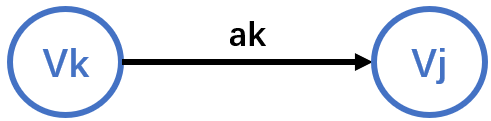
l(a_k) = vl(v_j) - Weight(v_k,v_j)

这里活动点v_k是事件a_k的前驱节点，活动点v_j是事件a_k的后继节点：

5.时间余量与关键活动的逻辑定义

通过上述定义，观察一个活动是否充裕我们就有了一个完美的定义，假如有一个活动a_k，现在l(a_k)=7h，e(a_k)=2h，我们能得到这个活动a_k什么信息呢？

活动a_k收到之前活动的影响，2h开始活动是它能开始活动的最早时间，但是它一定要2h如期开始干活吗？其实不然，它可以3h开始，4.5h开始，5.2h开始，它可以先玩几个小时，并不那么着急的。但是等到7h如果还没开始做，时间就有点来不及了，因为这个活动最迟必须要从7h开始。

所以这个活动余量就是：

timeMargin = l(a_k) - e(a_k)

发生刚刚上述这样情况的主要原因就是：a_k活动并不是关键活动，其延期并不影响全局活动的最终完成时间。

可以举个不恰当的例子，一群人沿着多条会不断相遇的轴线进行的马拉松比赛，当大家跑到一定会相遇的轴线交叉点时必须停下来等待所有其他人会和，会和完毕后再重新出发（全部人相遇完毕后立马出发）。这样刚好可以给某些人休息。

这场比赛 全部人完赛 的最少时间就是我们AOE工程需要完成的最小时间。

这时我们可以理解关键路径就是一个主轴（每次集体相遇后，接下来的路选择最长的那段），沿这条主轴跑的人永远是最累的人，因为他总是马不停蹄的地跑，到了轴线交叉点后大家一定早就都到了。

于是可见，要是在这条主轴上跑步的人决定了大家等待的时间，如果他在中途跑的时候休息了，那么大家一定会比预期多等他一段时间，那么总的“ 最短时间内大家一起跑完的目标 ”就延期了。

当然这个例子可能在一些细节上有瑕疵，总而言之想告诉大家的就是：
而关键活动的时间余量必须是0
从而引出关键路径的逻辑定义：
若存在一条从源点到汇点的活动序列<a₁,a₂,a₃,a₄, … ,a_n>，若有∀a_i满足l(a_i) - e(a_i)那么我们就定义这条路径为关键路径，其中，∀a_i都是关键活动。

三、代码构建

我们的代码构造过程主要是求解ve(v_k)与vl(v_k)的过程，e(a_k)与l(a_k)的求解是可选的，因为理论上可以仅仅通过结点的ve(v_k)与vl(v_k)来获取每个结点（事件）的时间余量，而可不必要于根据e(a_k)与l(a_k)求出每个边（活动）的时间余量。
这样的话，我们的最短路径就是点集而非边集。

1.求解ve(vk)与vl(vk)——解DAG

而ve(v_k)与vl(v_k)的求解是个典型的有向无环图固定起点的权值最优路径问题（解DAG）,是一个典型的动态规划问题，但是好在我们的状态转换方程在刚刚已经得到了：

公式一：ve(v_k) = Max{ ve(v_j) + Weight(v_j, v_k) }
这里的v_j是v_k的任意一个前驱节点，Weight(v_j, v_k)表示结点j与k之间的权值。

公式二：vl(v_k) = Min{ vk(v_j) - Weight(v_k, v_j) }
这里的v_j是v_k的任意一个后继节点，Weight(v_k, v_j)表示结点k与j之间的权值。

· 分析特殊值：
对于源点，默认的有ve(v_start) = 0，因为最早当前就可以开始事件。
同时，满足时间余量为0的不仅仅是活动，事件本身也满足这个原则，于是有关键路径上任何事件ve(v_i) - vl(v_i) = 0。又因为汇点一定在关键路径上，所以我们规定ve(v_end) = vl(v_end)。

· 解法思路：
这样一来我们发现了两轮动态规划过程，第一轮是利用ve(v_start) = 0从源点开始向汇点动态规划，利用公式一进行转移，最后求出ve(v_end)。第二轮，通过定义得到vl(v_end)，然后从汇点向源点动态规划，利用公式二进行转移。

· 关于选点：
点集选点不能选中间点，必须保证每次规划点的入度为0，因此我们必须利用拓扑排序遍历有关思路，通过入度为0的特性来找寻需要转移的结点（有向无环图动态规划的顺序符合拓扑排序顺序）。每次拓扑选点后，完成规划点到选择点的权值转移，之后删除选择点的入度，确保下次遍历能选中入度为0的新规划点。

· 第一轮转移
这里我们跳过一些非重点的数据结构声明过程，直接看下我们关系的核心代码。

		int[] tempEarliestTimeArray = new int[numNodes];
		for (int i = 0; i < numNodes; i++) {
			// This node cannot be removed.
			if (tempInDegrees[i] > 0) {
				continue;
			} // Of if

			System.out.println("Removing " + i);

			for (int j = 0; j < numNodes; j++) {
				if (weightMatrix.getValue(i, j) != -1) {
					tempValue = tempEarliestTimeArray[i] + weightMatrix.getValue(i, j);
					if (tempEarliestTimeArray[j] < tempValue) {
						tempEarliestTimeArray[j] = tempValue;
					} // Of if
					tempInDegrees[j]--;
				} // Of if
			} // Of for j
		} // Of for i

数组tempEarliestTimeArray是我们定义ve(v_k)的代码变量表现。
tempInDegrees统计的是每个结点的入度，定义tempInDegrees[i] = k 说明i号结点入度为k。
weightMatrix.getValue(i, j)，是自定义图对象中用于计算结点v_i与v_j之间的权值的方法。
最外层的for循环构造了一个进行拓扑排序的结构，每次的能顺利进入第二层循环的规划点都是能保证入度为0的结点。
其中：

		tempValue = tempEarliestTimeArray[i] + weightMatrix.getValue(i, j);
		if (tempEarliestTimeArray[j] < tempValue) {
			tempEarliestTimeArray[j] = tempValue;
		} // Of if

是转移方程的:

公式一：ve(v_k) = Max{ ve(v_j) + Weight(v_j, v_k) }
这里的v_j是v_k的任意一个前驱节点，Weight(v_j, v_k)表示结点j与k之间的权值。

代码表现，用max函数简写为：
tempValue = max(tempEarliestTimeArray[i] + weightMatrix.getValue(i, j), tempEarliestTimeArray[j])

注意：
因为要保证每次转移都有效果，我们需要考虑tempEarliestTimeArray数组的初始值问题，因为我们数组的值最小时0，也就是源点的值，但是之后的每个点因为受到了转移，初始值不可能是0，至少都要大于0，所以只要保证我们比较时的“tempEarliestTimeArray[j]”是0就好了，因为weightMatrix.getValue(i, j)永远是大于0的。

· 第二轮转移
完成第一轮转移后，第二轮转移就简单得多了，因为他们是对称的关系。但是要额外注意的一点是，因为我们是逆向规划，所以使用的是逆拓扑排序，因此不再使用入度数组进行统计，而是出度数组。

		for (int i = numNodes - 1; i >= 0; i--) {
			// This node cannot be removed.
			if (tempOutDegrees[i] > 0) {
				continue;
			} // Of if

			System.out.println("Removing " + i);

			for (int j = 0; j < numNodes; j++) {
				if (weightMatrix.getValue(j, i) != -1) {
					tempValue = tempLatestTimeArray[i] - weightMatrix.getValue(j, i);
					if (tempLatestTimeArray[j] > tempValue) {
						tempLatestTimeArray[j] = tempValue;
					} // Of if
					tempOutDegrees[j]--;
					System.out.println("The out-degree of " + j + " decreases by 1.");
				} // Of if
			} // Of for j
		} // Of for i

tempOutDegrees为出度数组。
其中

		tempValue = tempLatestTimeArray[i] - weightMatrix.getValue(j, i);
		if (tempLatestTimeArray[j] > tempValue) {
				tempLatestTimeArray[j] = tempValue;
		} // Of if

是转移方程:

公式二：vl(v_k) = Min{ vk(v_j) - Weight(v_k, v_j) } }
这里的v_j是v_k的任意一个后继节点，Weight(v_k, v_j)表示结点k与j之间的权值。

的代码表现，用min函数简写为：
tempValue = min(tempLatestTimeArray[i] - weightMatrix.getValue(j, i), tempLatestTimeArray[j])
注意：
因为要保证每次转移都有效果，我们仍然需要考虑tempLatestTimeArray数组的初始值问题，因为我们数组的值最大就是汇点的值endValue，但是之后的每个点因为受到了转移，值不可能大于等于endValue。因此，只要保证tempEarliestTimeArray数组值都为endValue，即可保证每次min计算时都有效，因为weightMatrix.getValue(i, j)永远是大于0的，tempLatestTimeArray[i] - weightMatrix.getValue(j, i)永远小于tempLatestTimeArray[i] - weightMatrix.getValue(j, i)。

2.通过时间余量得到最短路径

后续的操作就迎刃而解了，这里我们通过resultCriticalArray数组记录下符合时间余量（即tempEarliestTimeArray[i] == tempLatestTimeArray[i]）的结点下标，之后通过打印操作输出每个符合的结点。

		boolean[] resultCriticalArray = new boolean[numNodes];
		for (int i = 0; i < numNodes; i++) {
			if (tempEarliestTimeArray[i] == tempLatestTimeArray[i]) {
				resultCriticalArray[i] = true;
			} // Of if
		} // Of for i

		System.out.println("Critical array: " + Arrays.toString(resultCriticalArray));
		System.out.print("Critical nodes: ");
		for (int i = 0; i < numNodes; i++) {
			if (resultCriticalArray[i]) {
				System.out.print(" " + i);
			} // Of if
		} // Of for i
		System.out.println();

四、模拟与代码展示

/**
	 *********************
	 * The entrance of the program.
	 * 
	 * @param args
	 *            Not used now.
	 *********************
	 */
	public static void main(String args[]) {
		// A directed net without loop is required.
		// Node cannot reach itself. It is indicated by -1.
		int[][] tempMatrix3 = { { -1, 3, 2, -1, -1, -1 }, { -1, -1, -1, 2, 3, -1 },
				{ -1, -1, -1, 4, -1, 3 }, { -1, -1, -1, -1, -1, 2 }, { -1, -1, -1, -1, -1, 1 },
				{ -1, -1, -1, -1, -1, -1 } };
				
		Net tempNet3 = new Net(tempMatrix3);
		System.out.println("-------critical path");
		tempNet3.criticalPath();
	}// Of main

代码运行结果如下：

总结：

关键路径中涉及许多规划性的思想，这些思想是解决工程性计算机问题的关键思想。例如，当前结点的状态信息（最早，最迟发生时间等）的判断需要考虑多个前驱的因素，而这个结点本身又是后续若干结点的前驱信息，如此转移迭代构成了经典的动态规划问题。

然后针对图论本身来说，DAG图本身的结构决定了其需要涉及一些拓扑序列的入度与出度的判断思想，所以可以认为，关键路径是涉及图论中拓扑结构的多维动态规划问题中的典型问题。

往往来说DAG本身的转移特征非常明显，所以这种动态规划的设计也相对简单，可以像本文这样利用for循环枚举每个相邻结点进行转移，当然也使用记忆化搜索完成。

值得一提，除了这些能够看得见的特征，解决关键路径中使用的数组预先标记的策略也是一个很值得学习的方案：对于一个数组信息，若单次判断获取信息比较麻烦时，便可以把我们的需求分解为多个目标，就每个分解目标着手，分别通过构建for循环，用局部动态规划思想记录到标记数组A中。然后通过多次循环，逐个完成我们的每个分解目标于标记数组B、C、D…中。
最后，通过最后一个循环整合全部标记数组来辅助我们完成最终的信息获取，前人栽树后人乘凉，往往这最后的信息处理将会变得无比简单。

这有一个类似的使用这种思想的题目(来自leetcode)，读者们要是有兴趣不妨看下。

所以说，一个复杂而经典的算法不要仅看其耀眼的地方，认真品味之后，再看其细节，可以说浑身都是宝。