【三十五周】文献阅读：AlphaPose: 实时全身区域多人姿态估计与跟踪

摘要

AlphaPose作为首个实现全身多人实时姿态估计与追踪的系统，突破了传统方法在精度与效率上的双重局限。针对全身姿态估计中存在的尺度差异大、关键点定位精度不足等问题，研究团队提出对称积分关键点回归方法，通过改进传统热力图回归的梯度对称性，有效解决了手部、面部等精细部位定位的量化误差问题。系统采用参数化姿态非极大值抑制消除冗余检测框，引入姿态感知身份嵌入实现估计与追踪的联合优化。在训练策略上，通过部件引导提案生成器模拟真实检测框分布，结合多领域知识蒸馏整合跨数据集训练信息。实验表明，该系统在COCO-WholeBody、Halpe-FullBody等数据集上AP值提升超过5%，推理速度达到30FPS（使用YOLOv3检测器），较OpenPose等现有方法具有显著优势。该工作不仅发布了首个包含136个关键点的全身数据集，还开源了完整的系统框架，为行为分析、人机交互等应用提供了新基准。

Abstract

AlphaPose, as the first system to achieve real-time whole-body multi-person pose estimation and tracking, has broken through the dual limitations of accuracy and efficiency in traditional methods. To address issues such as large scale variations and insufficient keypoint localization accuracy in whole-body pose estimation, the research team proposed the Symmetric Integral Keypoint Regression (SIKR) method. By improving the gradient symmetry of traditional heatmap regression, SIKR effectively resolves the quantization error problem in locating fine-grained parts such as hands and faces. The system employs Parametric Pose Non-Maximum Suppression (P-NMS) to eliminate redundant detection boxes and introduces pose-aware identity embedding to jointly optimize estimation and tracking. In terms of training strategy, the system uses a Part-Guided Proposal Generator (PGPG) to simulate real detection box distributions and integrates cross-dataset training information through multi-domain knowledge distillation. Experiments show that the system achieves an AP improvement of over 5% on datasets such as COCO-WholeBody and Halpe-FullBody, with an inference speed of 30 FPS (using YOLOv3 detector), significantly outperforming existing methods like OpenPose. This work not only releases the first whole-body dataset containing 136 keypoints but also open-sources the complete system framework, providing a new benchmark for applications such as behavior analysis and human-computer interaction.

AlphaPose: 实时全身区域多人姿态估计与跟踪

---

Title: AlphaPose: Whole-Body Regional Multi-Person Pose Estimation and Tracking in Real-Time
Author: Hao-Shu Fang; Jiefeng Li; Hongyang Tang; Chao Xu; Haoyi Zhu; Yuliang Xiu
Source: IEEE Transactions on Pattern Analysis and Machine Intelligence
Link: https://ieeexplore.ieee.org/abstract/document/9954214/authors#authors

---

研究背景

人体姿态估计作为计算机视觉基础任务，在动作识别、影视制作等领域具有重要价值。传统方法聚焦于躯干关键点检测，但实际应用中需要同时捕捉面部表情、手势变化等全身信息。

现有方案存在三大瓶颈：其一，热力图方法受限于分辨率导致手部等小尺度部位定位误差显著；其二，多阶段处理框架（检测+姿态估计）存在误差累积，检测失败直接导致姿态丢失；其三，现有数据集缺乏全身标注，跨数据集训练面临域适应挑战。

早期工作如OpenPose采用级联网络分别处理身体、手部和面部，但计算冗余严重。HRNet等热力图方法在躯干检测表现优异，却难以应对手指关节等微动作。ZoomNet通过ROIAlign放大特征虽提升精度，但特征重采样带来额外计算负担。同时，现有追踪方法多依赖时序连续性，在快速运动场景易出现身份跳变。这些局限促使研究者寻求端到端的解决方案，在保证精度的同时实现实时处理。

方法论

本研究采用了基于 HRNet 的高分辨率特征提取网络作为基础架构，结合了 PGA (姿势引导注意力)模块和 MSIM (多尺度信息融合)模块。HRNet 能够有效捕捉不同尺度的空间信息，而 PGA 则专注于增强目标人物区域的关注度，减少背景干扰。MSIM 模块负责将来自不同层次的信息进行融合，从而提高了最终的姿态估计和跟踪效果。此外，作者还进行了详尽的消融实验，验证了各个组件的有效性。

AlphaPose 采用改进的Top-Down框架，首先检测人体边界框，然后独立估计每个框内的姿势。对于自顶向下的方法而言，尽管它们的性能在常见的基准测试中领先，但这种方法有几个显著的缺点。第一是如果目标检测器失效，那么就无法进行正确的姿态估计，第二是当前研究者为了准确性而采用准确度比较高的人体检测器，这使得两阶段处理在姿态估计中变慢。 为了解决自顶向下框架的这些缺点，研究者提出了一种新的方法，以使其在实践中高效和可靠。为了减轻漏检测问题，他们降低了检测置信度和NMS阈值，以提供更多的候选检测。在此基础上，还提出了一种新的姿态距离度量方法来比较姿态的相似性，并通过参数化姿态NMS消除冗余框中的冗余姿态。采用数据驱动的方法对姿态距离参数进行优化。研究者表明，采用这种策略的基于YOLOV3SPP检测器的自顶向下框架可以实现与最先进的检测器相当的性能，同时实现更高的效率。此外，为了提高自顶向下框架在推理过程中的速度，研究者在AlphaPose中设计了一个多级并发流水线，使框架能够实时运行。

对于自然环境下的全身姿态估计还面临几个额外的问题。无论是采取自顶向下还是自底向上的方法，目前最常用的关键点表示都是heatmap。但由于计算资源的限制，heatmap尺寸通常是输入图像的四分之一。然而，对于同时定位身体、面部和手的关键点，这种表示是不合适的，因为它无法处理不同身体部位的大规模变化。正如上图所示，由于heatmap表示是离散的，heatmap上的两个相邻网格都可能错失正确位置。这对body姿态估计来说不是问题，因为正确的区域通常很大。然而，对于手和面部的精细关键点，很容易错失正确位置。

整体框架

上图表示AlphaPose的工作流程：首先利用现成目标检测模型比如YOLOv3进行人体检测，获取一系列包含人体位置信息的边界框，这些边界框以四维坐标$(x,y,w,h)$的形式表示。接下来，依据这些边界框对原始图像进行裁剪和尺寸调整，确保每个被裁剪出的人体图像都能以统一大小输入到姿态估计网络中。随后，裁剪好的图像将通过名为FastPose的高效姿态估计网络进行分析得到全身热图和Re-ID特征，并采用一种称为对称积分关键点回归的方法从生成的热图中精确提取人体的关键点位置。为了去除重复的姿态估计结果，系统运用了姿态非极大值抑制技术来筛选并合并相近的姿态，减少误报。为进一步提升姿态识别精度，AlphaPose引入了一个姿势引导注意力模块（PGA），该模块能够根据预测的人体姿态优化re-ID特征提取过程，使得提取出的特征更加专注于人体本身而非背景干扰。最后，通过多阶段身份匹配算法，结合人体姿态、优化后的re-ID特征以及初始检测框的信息，系统能够为每个人分配一个唯一的跟踪标识，从而在复杂的多人场景中实现精准的个体跟踪。经过这一系列步骤，AlphaPose可以准确输出各个个体的关键点位置及其姿态信息，完成对复杂场景下多人姿态的有效估计与跟踪。

模块组成

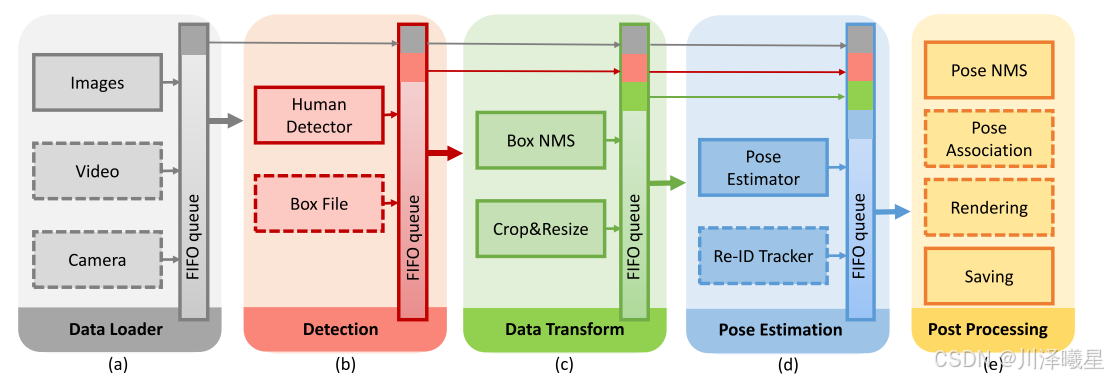
AlphaPose的系统架构分为五个模块，即（a）数据加载模块，可以将图像、视频或相机流作为输入；（B）检测模块，提供人的建议；（c）数据变换模块，处理检测结果并为后续模块裁剪每个人；（d）姿态估计模块，为每个人生成关键点；（e）后处理模块，用于处理并保存姿态结果。

骨干网络

AlphaPose中的骨干网络名为FastPose，旨在实现高精度和高效率的姿态估计。其核心结构基于ResNet（如ResNet-50或ResNet-101），用于从输入的裁剪图像中提取特征。为了进一步提升特征的分辨率，FastPose引入了三个Dense Upsampling Convolution (DUC)模块。DUC模块首先对特征图（维度为 h×w×c）进行二维卷积操作，然后通过PixelShuffle操作将特征图重塑为更高分辨率的
2h×2w×c 。最后，经过一个1×1 卷积层生成关键点热图（heatmaps）。这种设计通过DUC模块实现了高效的特征上采样，同时保留了丰富的空间信息，从而在姿态估计任务中实现了高精度和高效率的平衡。

@SPPE.register_module
class FastPose(nn.Module):  # 定义FastPose类，继承自nn.Module

    def __init__(self, norm_layer=nn.BatchNorm2d, **cfg):  # 初始化函数，接收norm_layer和配置参数
        super(FastPose, self).__init__()  # 调用父类构造函数
        self._preset_cfg = cfg['PRESET']  # 获取预设配置
        if 'CONV_DIM' in cfg.keys():  # 如果配置中有CONV_DIM键
            self.conv_dim = cfg['CONV_DIM']  # 设置卷积维度
        else:
            self.conv_dim = 128  # 默认卷积维度为128
        if 'DCN' in cfg.keys():  # 如果配置中有DCN键
            stage_with_dcn = cfg['STAGE_WITH_DCN']  # 获取各阶段是否使用DCN的信息
            dcn = cfg['DCN']  # 获取DCN配置
            self.preact = SEResnet(f"resnet{cfg['NUM_LAYERS']}", dcn=dcn, stage_with_dcn=stage_with_dcn)  # 创建SEResnet实例
        else:
            self.preact = SEResnet(f"resnet{cfg['NUM_LAYERS']}")  # 不使用DCN创建SEResnet实例

        # Imagenet预训练模型加载
        import torchvision.models as tm   # noqa: F401,F403  # 导入torchvision中的模型模块
        assert cfg['NUM_LAYERS'] in [18, 34, 50, 101, 152]  # 确保NUM_LAYERS在支持的范围内
        x = eval(f"tm.resnet{cfg['NUM_LAYERS']}(pretrained=True)")  # 加载对应层数的预训练ResNet模型

        model_state = self.preact.state_dict()  # 获取当前模型的状态字典
        state = {k: v for k, v in x.state_dict().items()  # 从预训练模型中选择匹配的参数
                 if k in self.preact.state_dict() and v.size() == self.preact.state_dict()[k].size()}
        model_state.update(state)  # 更新当前模型的状态字典
        self.preact.load_state_dict(model_state)  # 将更新后的状态字典加载到模型中

        self.suffle1 = nn.PixelShuffle(2)  # 定义PixelShuffle层，用于上采样
        self.duc1 = DUC(512, 1024, upscale_factor=2, norm_layer=norm_layer)  # 定义第一个DUC层
        if self.conv_dim == 256:  # 根据卷积维度设置第二个DUC层
            self.duc2 = DUC(256, 1024, upscale_factor=2, norm_layer=norm_layer)
        else:
            self.duc2 = DUC(256, 512, upscale_factor=2, norm_layer=norm_layer)
        self.conv_out = nn.Conv2d(self.conv_dim, self._preset_cfg['NUM_JOINTS'], kernel_size=3, stride=1, padding=1)  # 输出层

    def forward(self, x):  # 定义前向传播过程
        out = self.preact(x)  # 通过主干网络
        out = self.suffle1(out)  # 上采样
        out = self.duc1(out)  # 第一个DUC层
        out = self.duc2(out)  # 第二个DUC层

        out = self.conv_out(out)  # 最终输出层
        return out  # 返回最终输出

    def _initialize(self):  # 初始化权重方法
        for m in self.conv_out.modules():  # 遍历输出层的所有模块
            if isinstance(m, nn.Conv2d):  # 如果是卷积层
                # 使用正态分布初始化权重
                nn.init.normal_(m.weight, std=0.001)
                nn.init.constant_(m.bias, 0)  # 初始化偏置为0

对称积分关键点回归

热图是人体姿态估计领域中关节定位的主要表示。热图的读出位置是离散的数字，因为热图仅描述了在每个空间网格中出现关节的可能性，这导致不可避免的量化误差。此前研究者认为基于soft-argmax的积分回归更适合全身关键点定位。但在本文中作者提出了一种新的关键点回归方法，具有更高的精度，并且表现出良好的性能。

soft-argmax操作，也称为积分回归，是可微分的，它将基于热图的方法转换为基于回归的方法，并允许端到端训练。积分回归运算定义为：
$$\hat{\mu }=\sum x\cdot p_x$$
其中 $x$ 是每个像素的坐标，$p_x$ 表示归一化后热图上的像素概率。在训练过程中，损失函数用于最小化预测关节位置 $\hat{\mu }$ 和真实位置 $\mu$ 之间的 ${\ell }_1$ 范数：${\mathcal{L}}_{reg}=\Vert \mu -\hat{\mu }{\Vert }_1$。每个像素的梯度可以表示为：
$$\frac{\partial {\mathcal{L}}_{reg}}{\partial p_x}=x\cdot \text{sgn}(\hat{\mu }-\mu ).$$

在这个公式中可以看出梯度幅度是不对称的。梯度的绝对值由像素的绝对位置（即 $x$）决定，而不是相对于真实值的相对位置。这意味着在给定相同的距离误差时，关键点位于不同位置时梯度会有所不同。这种不对称性破坏了 CNN 网络的平移不变性，从而导致性能下降。

因此，研究者们需要找到一种幅度对称的梯度函数，如下所示，这个函数是真实梯度的近似：

$${\delta }_{ASG}=A_{grad}\cdot \text{sgn}(x-\hat{\mu })\cdot \text{sgn}(\hat{\mu }-\mu )$$

其中 $A_{grad}$ 表示梯度的幅度。我们手动将其设置为热图大小的 1/8，并在下一段中给出推导。使用我们的对称梯度，梯度分布集中在预测的关节位置 $\hat{\mu }$ 处。在学习过程中，这种对称的梯度分布可以更好地利用热图的优势，并以更直接的方式逼近真实位置。例如，假设预测位置 $\hat{\mu }$ 高于真实位置 $\mu$。一方面，网络倾向于抑制 $\hat{\mu }$ 右侧的热图值，因为它们具有正梯度；另一方面，由于负梯度的影响，$\hat{\mu }$ 左侧的热图值会被激活。

$A_{grad}$ 的推导

在这里，我们进行 Lipschitz 分析以推导 $A_{grad}$ 的值，并展示 ASG 可以为训练提供更稳定的梯度。回忆一下，$f$ 表示我们想要最小化的目标函数。我们说 $f$ 是 $L$-平滑的，如果：

$$\Vert {\nabla }_{\theta }f(\theta +\Delta \theta )-{\nabla }_{\theta }f(\theta )\Vert \le L\Vert \Delta \theta \Vert ,$$

其中 $\theta$ 是网络参数，$\nabla$ 表示梯度。目标函数可写成：

$${\nabla }_{\theta }f={\nabla }_{\theta }\mathcal{L}(\mu ,h(z))={\nabla }_z\mathcal{L}(\mu ,h(z)){\nabla }_{\theta }z,$$

其中 $z$ 表示网络预测的 logits，$\hat{\mu }=h(z)$ 表示归一化和 soft-argmax 函数的组合。这里，我们假设网络的梯度是平滑的，只分析组合函数，即：

$$\Vert {\nabla }_z\mathcal{L}(\mu ,h(z+\Delta z))-{\nabla }_z\mathcal{L}(\mu ,h(z))\Vert .$$

在传统的积分回归中，我们有：

$${\nabla }_z\mathcal{L}(\mu ,h(z))=(x-\hat{\mu })\cdot p_x.$$

在这种情况下，$\Vert {\nabla }_z\mathcal{L}(\mu ,h(z+\Delta z))-{\nabla }_z\mathcal{L}(\mu ,h(z))\Vert$等价于：

$$\Vert (x-\hat{\mu }-\Delta \hat{\mu })(p_x+\Delta p_x)-(x-\hat{\mu })\cdot p_x\Vert .$$

注意 $x$ 可以是热图上的任意位置。设热图大小为 $W$，则在整个数据集上 $\Vert x-\hat{\mu }\Vert \le W$。因此，我们推导出积分回归的 Lipschitz 常数：

$$\begin{array}{rl}& \Vert {\nabla }_z\mathcal{L}(\mu ,h(z+\Delta z))-{\nabla }_z\mathcal{L}(\mu ,h(z))\Vert \\ & \le \Vert W(p_x+\Delta p_x)-W{p}_x\Vert =W\Vert \Delta p_x\Vert \\ & =W\cdot L_s\cdot \Vert \Delta z\Vert ,\end{array}$$

其中 $L_s$ 是归一化函数的 Lipschitz 常数 。这表明传统的积分回归将一个因子 $W$ 乘到归一化的 Lipschitz 常数上。

同样，我们可以推导出提出的幅度对称函数的 Lipschitz 常数。首先，logits 的梯度是：

$$\begin{array}{rl}|{\nabla }_z\mathcal{L}(\mu ,h(z))|& =|A_{grad}\cdot p_x\cdot (1+\sum _{x_i<\hat{\mu }}{p}_{x_i}-\sum _{x_i>\hat{\mu }}{p}_{x_i})|\\ & \le 2\cdot A_{grad}\cdot p_x.\end{array}$$

我们设置 $A_{grad}=W/8$，使得梯度的平均范数与积分回归相同。具体来说，

$$E_x[(x-\hat{\mu })p_x]=E_x[|x-\hat{\mu }|]p_x=\frac{W}{4}\cdot p_x.$$

提出的幅度对称函数的 Lipschitz 常数推导如下：

$$\begin{array}{rl}& \Vert {\nabla }_z\mathcal{L}(\mu ,h(z+\Delta z))-{\nabla }_z\mathcal{L}(\mu ,h(z))\Vert \\ & \le \Vert 2A_{grad}(p_x+\Delta p_x)-2A_{grad}{p}_x\Vert =\frac{W}{4}\Vert \Delta p_x\Vert \\ & =\frac{W}{4}\cdot L_s\cdot \Vert \Delta z\Vert .\end{array}$$

姿态引导注意机制

re-ID特征可以用于从大量人体中中识别同一个体。在自上而下框架中，可以从对象检测器产生的每个边界框中提取re-ID特征。然而，re-ID特征的质量会受到边界框内背景的影响，特别是在存在其他人身体的情况下。为了解决这个问题，作者考虑使用预测的人体姿态来构建一个区域，在该区域中人体集中。因此，提出了姿势引导注意力（PGA），以迫使提取的特征集中在感兴趣的主体人体上，并忽略背景的影响。

姿态估计器生成 $k$ 个热图，其中 $k$ 表示每个人的关键点数量。然后 PGA 模块将这些热图转换为注意力图 $(m_A)$，通过简单的卷积层实现。请注意，$m_A$ 与再识别特征图 $(m_{id})$ 具有相同的大小。因此，我们可以获得加权的再识别特征图 $(m_{wid})$：

$$m_{wid}=m_{i}d\odot m_A+m_{i}d$$

其中 $\odot$表示 Hadamard 乘积。

最后，身份嵌入$(em{b}_{id})$ 是一个128维向量，由全连接层编码。

创新性

1. 对称积分关键点回归
   突破传统热力图的离散定位局限，设计双阶段归一化机制：首先通过Sigmoid生成置信热力图保留尺寸不变性，再经全局归一化得到概率分布。改进的梯度计算方式使反向传播时梯度幅值对称于预测点，较传统积分回归的线性梯度更符合CNN平移不变特性。数学推导证明该方法将Lipschitz常数降低至原方法的1/4，提升优化稳定性。实验显示该设计使手部关键点AP提升3.2%。

2. 多模态联合优化
   参数化P-NMS构建姿态相似度度量函数，融合关键点匹配度与空间相似度，通过数据驱动优化阈值参数。PGPG模块分析检测框偏移分布，生成符合真实场景的增强样本，缓解检测-估计域差异。多领域知识蒸馏整合300W（面部）、FreiHand（手部）等专项数据集，在特征空间实现跨域对齐。

3. 姿态感知追踪框架
   在姿态估计网络并行接入Re-ID分支，通过姿态引导注意力抑制背景干扰。多阶段身份匹配（MSIM）融合检测框IOU、归一化姿态距离与外观特征，构建分层关联策略。联合训练时采用损失平衡机制，在PoseTrack等视频数据上交替优化姿态与身份损失。

实验结果

在Halpe-FullBody测试集上，FastPose50-dcn-si模型以48.4% AP全面超越OpenPose（28.1%）和ZoomNet（42.7%），手部检测AP提升62%。

COCO-WholeBody对比显示，该方法在384×288输入下全身AP达57.7%，较HRNet提升14.5个百分点。

追踪方面，联合训练模型在PoseTrack2018验证集取得74.7% mAP，处理速度达8.7FPS，较FlowTrack快2.9倍。效率测试表明，系统在20人场景下仍保持25FPS，满足实时交互需求。

关键消融实验验证：双阶段热图归一化使手部AP提升6%，PGPG数据增强带来1.3%整体增益。

姿态注意力使Re-ID特征区分度提升17%。误差分析显示，92%的失败案例源于严重遮挡，仅3.7%由定位误差导致。

局限性

尽管取得显著进展，系统仍存在以下局限：

​检测依赖：Top-Down框架本质受限于检测器性能，在密集人群场景（如超过50人）可能出现漏检。
​标注成本：136关键点标注耗时达传统方法的4倍，Halpe数据集规模仅为COCO的20%。
​动态适应：当前模型对运动模糊处理不足，视频测试集上追踪中断率较图像高11%。
​3D扩展：缺乏深度信息导致无法区分空间重叠的相似姿态。

针对第一个局限性，可以尝试使用更强大的检测器减少漏检现象，或者采取动态检测策略，在密集区域增加检测框生成密度，稀疏区域减少检测框数量，平衡精度与效率。

而第二个局限性可以采用数据增强来增加可训练的数据集，或者是引入对比学习策略，利用未标注数据增强特征表示。

第三个局限性可以引入时序卷积网络（TCN）或Transformer，捕捉帧间运动模式，平滑关键点轨迹。

最后一个局限性可以结合3D人体姿势估计方法，比如结合SimpleBaseline3D或VideoPose3D，将2D关键点升维至3D空间，解决深度模糊性。

总结

AlphaPose 是一个实时多人全身姿态估计与跟踪系统，旨在通过一系列创新技术解决传统姿态估计中的挑战。论文提出了对称积分关键点回归（SIKR）以实现精确的关键点定位，参数化姿态非极大值抑制（P-NMS）用于消除冗余检测，以及姿态感知身份嵌入以联合进行姿态估计与跟踪。此外，论文还引入了部分引导的提议生成器（PGPG）和多领域知识蒸馏来提升模型的泛化能力。实验表明，AlphaPose 在多个数据集上（如 COCO-WholeBody、PoseTrack 等）在速度和精度上均优于现有方法，并发布了开源代码和数据集以促进相关研究。