算法设计与分析基础 第十章谜题

习题10.1

8.我们是不是能应用单纯形法来解决背包问题（参见6.6节的例2）？如果你认为能，请指出这是不是一个解决该问题的好算法；如果你认为不能，请说明原因。

解答：可以通过单纯形法解决背包问题的连续版本，因为它是一般线性规划问题的一个特例（见6.6节中的例2）。 然而，它不是解决这个问题的好方法，因为它可以通过基于贪婪法的更简单的算法更有效地解决。由于对问题变量施加的完整性（0-1）约束，单纯形法无法解决0-1版本的背包问题。

 

10.如果线性规划问题

是主问题，它的对偶问题是

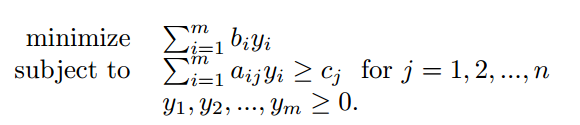
a. 用矩阵的符号来表示主问题和对偶问题。、

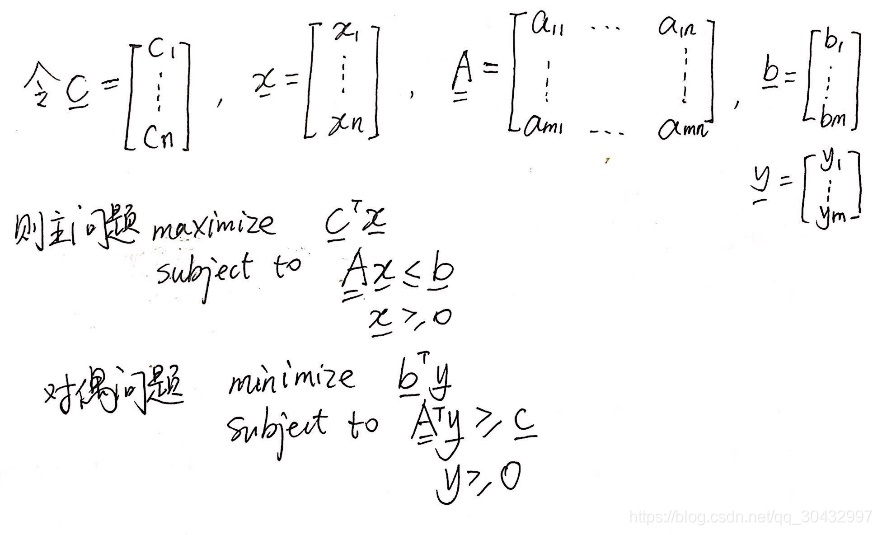
b.求下列线性规划问题的对偶问题。

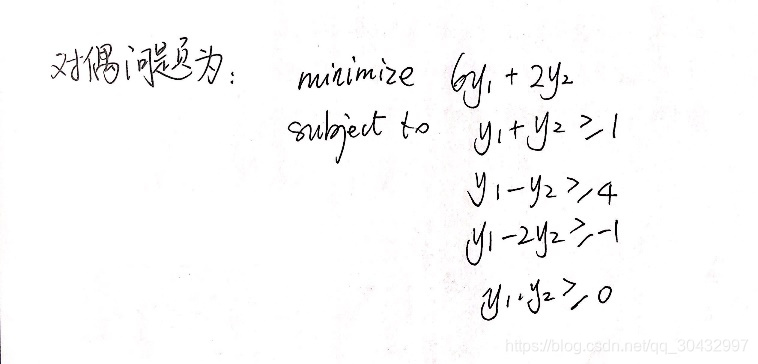
c.解上述主问题和对偶问题，并比较它们的目标函数的最优值。

 

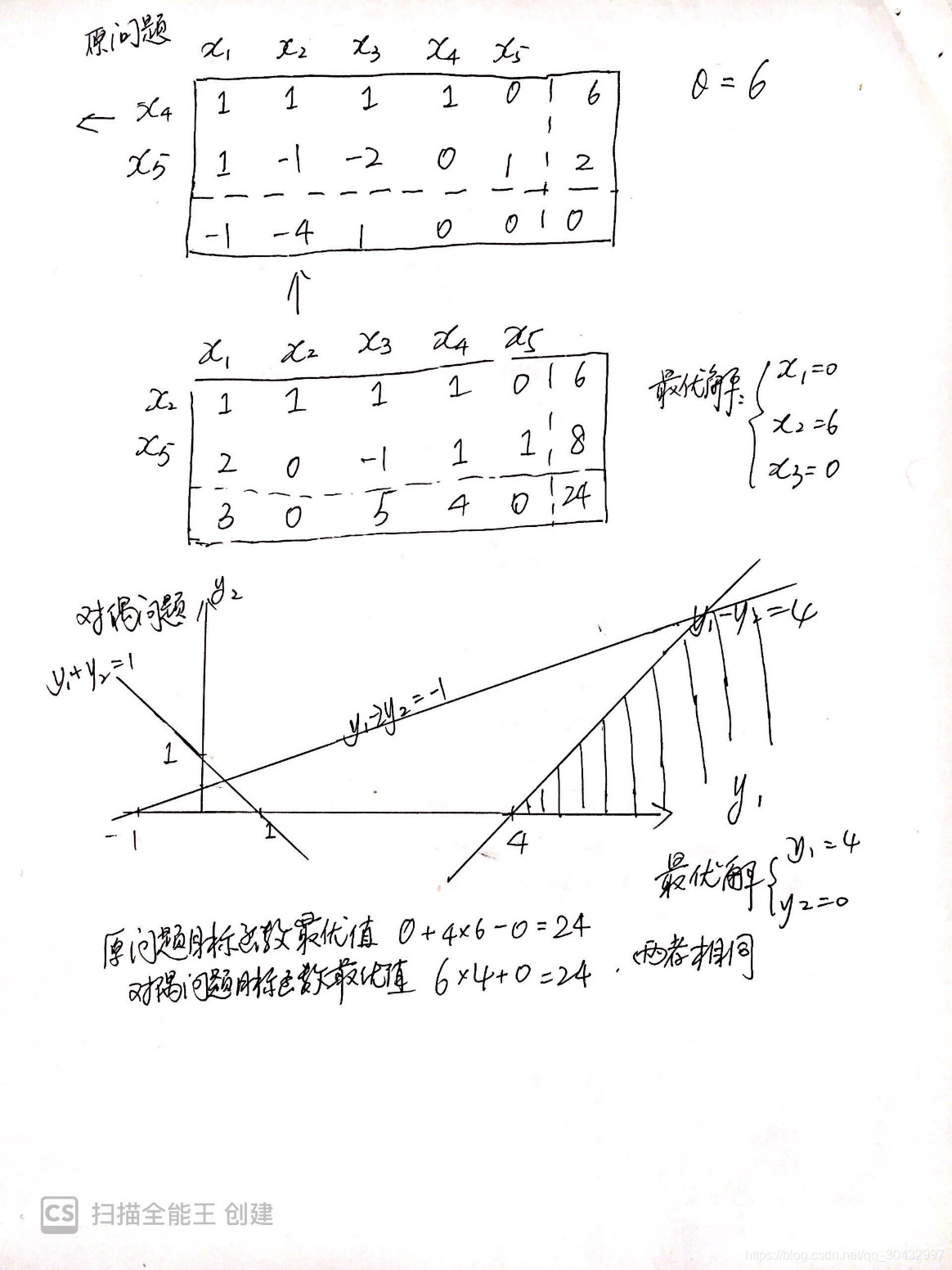
习题10.2

2b.对下列网络用最短增益路径算法求它们的最大流和最小割。

 

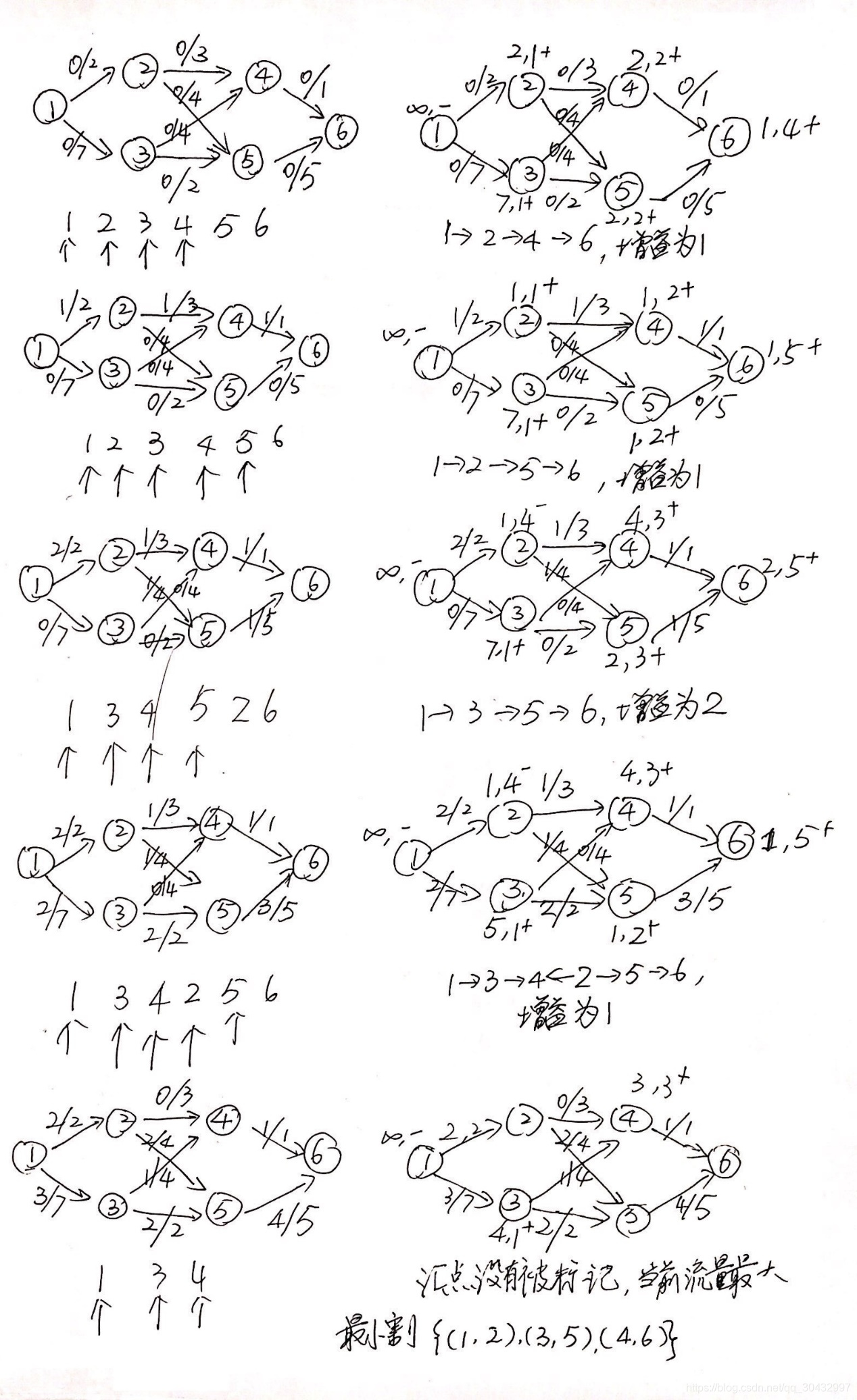
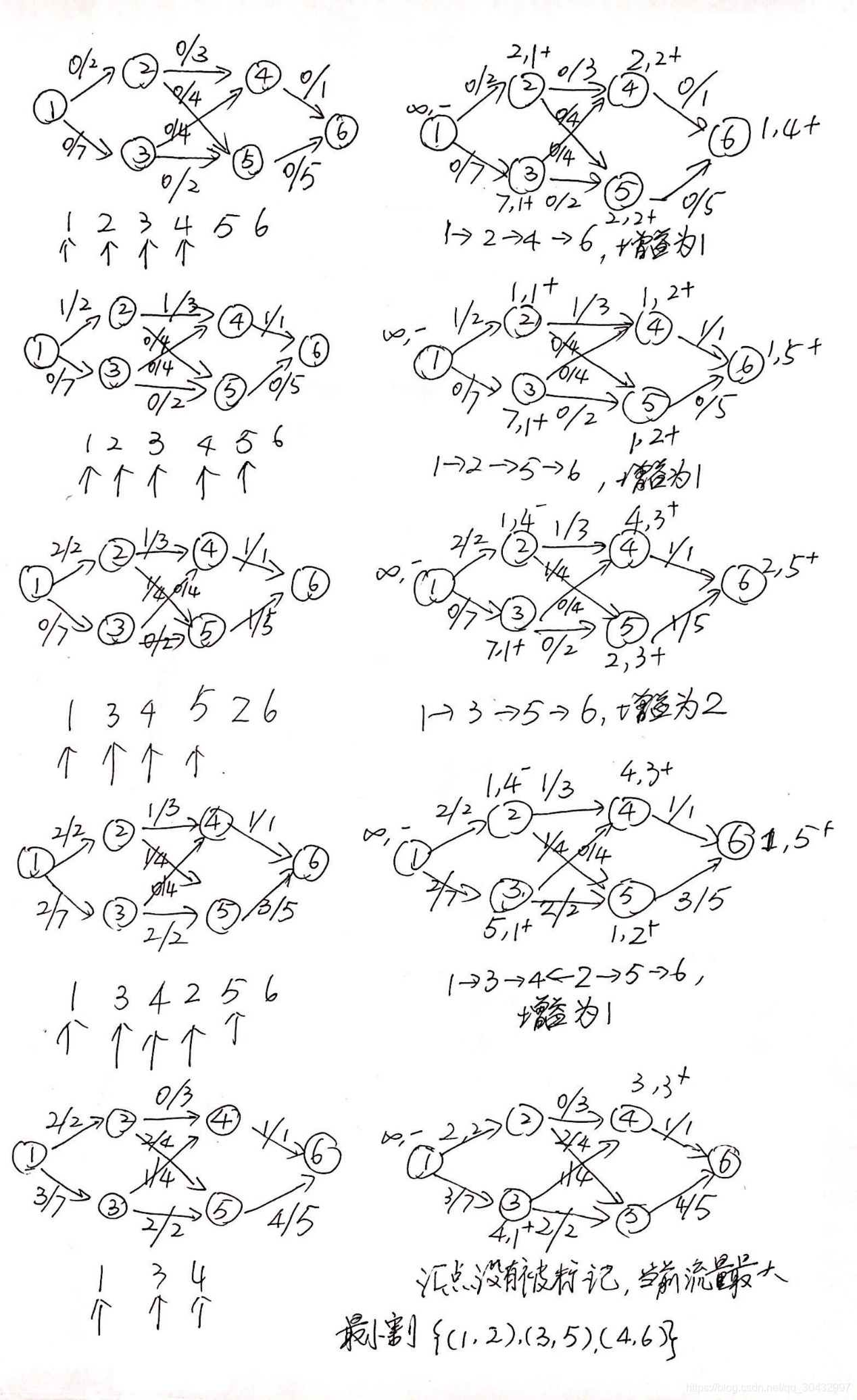
4a.对于网络中有多个源点和汇点的最大流量问题，如何能将其转化为具有一个源点和汇点的等价问题？

解答：将两个顶点添加到网络中，分别作为新的源点和汇点。将新源点与每个原始源点相连，新汇点与每个原始汇点相连，这些边的容量应保证足够大。

 

 

 

10.就餐问题 几个家庭一起外出就餐。为了增进社交，他们希望同一个家庭的人不要坐在一张桌子上。试述如何利用最大流量问题找到一个满足要求的座位排法（或者证明这种排法不存在）。假设该就餐团共有p个家庭，第i个家庭有ai个成员。还假设有q张桌子，第j张桌子的座位容量是bj。

解答：对以下网络求最大流问题。如果最大流量值等于a1+a2+…+ap，那么问题有解；否则，该问题无解。

习题10.3

10.多米诺谜题 多米诺是一块2×1的方块，方向上既可以水平放置，也可以垂直放置。一块由多个1×1的格子组成的板，如果正好用多米诺覆盖，而且没有重叠，则称为一个覆盖。对于1块8×8的板，是不是可以用多米诺覆盖，并使得对角的两个格子不被覆盖？

解答：对角两个格子不被覆盖是做不到的。可以把格子看作是一个8×8棋盘（在对角线对角处有两个缺失的正方形），棋盘的方块交替上下黑色和白色。每个多米诺骨牌将完全覆盖（匹配）一个黑色和一个白色正方形，因为它有32个正方形和30个正方形分别处于不同颜色，所以无法覆盖。

 

习题10.4

2.设计一个简单的算法来检查一个给定的婚姻匹配是否稳定，并确定它的时间效率类型。

婚姻匹配稳定检查算法

输入：一个婚姻匹配M，包含n对匹配

输出：若稳定返回“yes”，否则返回一对不稳定的匹配

for 男士m←1 to n do

       for 男士m更优先选择的每个女士w（相比于M中m的匹配）do

              if 女士w更优先选择男士m（相比于M中w的匹配）

                      return (m,w)

return “yes”

该算法的时间效率为O(n^2)

 

10.考虑室友问题，该问题和稳定婚姻问题相关但更难：“偶数个男孩要分成一对对室友。在配对的集合中，如果有两个男孩不是室友，但相对现在室友他们更希望分在一起，那么该集合是不稳定的，反之 ，该集合是稳定的。”给出该问题的一个实例，使得该实例不存在稳定的配对。

解答：以下使该问题的一个实例。

男孩	1st	2nd	3rd
A	B	C	D
B	C	A	D
C	A	B	D
D	*	*	*

(A,B), (C,D):  BC更希望分在一起

(A,C), (B,D):  AB更希望分在一起

(B,C), (A,D):  AC更希望分在一起