模型量化论文阅读#2----BRECQ: PUSHING THE LIMIT OF POST-TRAINING QUANTIZATION BY BLOCK RECONSTRUCTION

2021/5/20 10：31 第一次编辑；

1. 相关基础

量化基础知识

在量化中，一个比较重要的概念是量化函数$q(\cdot )$，即如何从一个浮点数值映射到具有特定宽度的量化值，即: $q(\cdot ):\mathcal{R}\to {\mathcal{Q}}_b^{\text{u,sym }}$. 一般比较常用的量化函数是四舍五入函数，当前很多量化算法使用的是这个函数，比如PACT等。

一般量化问题可以表示为下述的优化目标函数：
$\min \Vert \hat{\mathbf{w}}-\mathbf{w}{\Vert }_F^2.$ s.t. $\hat{\mathbf{w}}\in {\mathcal{Q}}_b^{\mathrm{u},\text{ sym }}$

$\hat{\mathbf{w}}$ 表示量化后的权重，$\mathbf{w}$表示原始的浮点值的权重。

${\mathcal{Q}}_b^{\mathrm{u},\text{ sym }}$ 表示的是对称均匀量化时的量化值，一般为

${\mathcal{Q}}_b^{\mathrm{u},\mathrm{s}\mathrm{y}\mathrm{m}}=s\times \left\{-2^{b-1},\dots ,0,\dots ,2^{b-1}-1\right\}$。

s表示step size，b是量化的bit width。

上述的目标函数是对已经训练好的模型的参数直接进行量化，然后最小化量化参数与原始已经优化好的参数之间的量化误差，这种方式一般称为训练后量化。但是，有相关研究表明，最小化参数空间的量化误差并不能直接带来量化后网络的最佳的性能。 此时，有研究表明可以在量化感知训练（QAT）中采用梯度下降的方式学习step size参数 s，其直接采用网络的损失作为目标函数进行训练，如下：
$$\min \mathbb{E}[L(\hat{\mathbf{w}})],\text{ s.t. }\hat{\mathbf{w}}\in {\mathcal{Q}}_b^{\mathrm{u},\mathrm{s}\mathrm{y}\mathrm{m}}.(1)$$
虽然这种方式能够得到更好的量化后模型性能，但是存在以下问题：
如果没有端到端的微调训练，如果没有足够的训练数据，如果没有足够的训练资源，
学习到足够优化的量化后权重并不容易。也就是这种量化方法更加依赖训练，更加耗费计算资源和训练时间。

泰勒展开

对权重的量化无非就是将一个给定的浮点值向上或者向下重新赋值为一个新的值，就以最简单的四舍五入为例，假设某个浮点数F，其量化后的值无非就是$\lfloor F\rfloor$ 或者$\lfloor F\rfloor +1$。有研究认为可以将这种量化看作是加在权重上的一种扰动。为了分析量化带来的模型损失（性能）带来的退化，可以应用泰勒展开对此进行分析，如下：
$$\mathbb{E}[L(\mathbf{w}+\Delta \mathbf{w})]-\mathbb{E}[L(\mathbf{w})]\approx \Delta {\mathbf{w}}^{\top }{\overline{\mathbf{g}}}^{(\mathbf{w})}+\frac{1}{2}\Delta {\mathbf{w}}^{\top }{\overline{\mathbf{H}}}^{(\mathbf{w})}\Delta \mathbf{w}.(2)$$
其中，${\overline{\mathbf{g}}}^{(\mathbf{w})}=\mathbb{E}\left[{\nabla }_{\mathbf{w}}L\right]$ ， ${\overline{\mathbf{H}}}^{(\mathbf{w})}=\mathbb{E}\left[{\nabla }_{\mathbf{w}}^{2}L\right]$ 分别表示损失函数关于权重的梯度和海森矩阵（由二阶导数构成的矩阵），$\Delta \mathbf{w}$代表权重的扰动。

另外，我们是针对已经优化好的权重进行分析的，对优化好的权重其一阶导数可以认为是0，因为此时其应该是处于局部最优点的。所以上述公式中可以只考虑包含海森矩阵的第二项。

然后论文指出，因为网络中包含的参数量过于庞大，如果直接计算这种大规模参数的海森矩阵是十分占用内存的，为了解决这种问题，论文提出了两个假设，如下（还不是很懂）：

2. 该论文的量化方法

2.1 层间依赖性

做一些符号描述： 假设网络共有n层，网络参数表示为$\theta$, $\theta$表示为一种向量的形式，即将每一层的权重参数展开成一维向量的形式，然后将n层的参数堆叠而形成最终的参数，$\theta =\mathrm{vec}{\left[{\mathbf{w}}^{(1),\top },\dots ,{\mathbf{w}}^{(n),\top }\right]}^{\top }$。假设 $\theta$的维度是d。网络的输出表示为${\mathbf{z}}^{(n)}=f(\theta )$，假设${\mathbf{z}}^{(n)}$的维度是m。 损失函数表示为$L(f(\theta ))$。损失函数关于参数$\theta$的海森矩阵可以通过下式进行计算：
$$\frac{{\partial }^{2}L}{\partial {\theta }_i\partial {\theta }_j}=\frac{\partial }{\partial {\theta }_j}\left(\sum _{k=1}^m\frac{\partial L}{\partial {\mathbf{z}}_k^{(n)}}\frac{\partial {\mathbf{z}}_k^{(n)}}{\partial {\theta }_i}\right)=\sum _{k=1}^m\frac{\partial L}{\partial {\mathbf{z}}_k^{(n)}}\frac{{\partial }^2{\mathbf{z}}_k^{(n)}}{\partial {\theta }_i\partial {\theta }_j}+\sum _{k,l=1}^m\frac{\partial {\mathbf{z}}_k^{(n)}}{\partial {\theta }_i}\frac{{\partial }^{2}L}{\partial {\mathbf{z}}_k^{(n)}\partial {\mathbf{z}}_l^{(n)}}\frac{\partial {\mathbf{z}}_l^{(n)}}{\partial {\theta }_j}（3）$$
这里的公式推导主要就是基本的微积分中的求导公式。
同样的，对于一个已经训练好的收敛的模型来说，损失函数关于参数的一阶导数应该可以认为是0的，所以第一项可以忽略。

所以，只看第二项的话，损失函数$L$关于参数$\theta$的海森矩阵可以表示为：
$${\mathbf{H}}^{(\theta )}\approx {\mathbf{G}}^{(\theta )}={\mathbf{J}}_{{\mathbf{z}}^{(n)}}(\theta {)}^{\top }{\mathbf{H}}^{\left({\mathbf{z}}^{(n)}\right)}{\mathbf{J}}_{{\mathbf{z}}^{(n)}}(\theta )（4）$$

下面，针对二次型$\Delta {\theta }^{\top }{\mathbf{H}}^{(\theta )}\Delta \theta$，它可以表达为下面的形式：
$$\Delta {\theta }^{\top }{\mathbf{H}}^{(\theta )}\Delta \theta =\sum _{i=1}^d\Delta {\theta }_i^2\left(\frac{{\partial }^{2}L}{\partial {\theta }_i^2}\right)+2\sum _{i<j}^d\Delta {\theta }_i\Delta {\theta }_j\frac{{\partial }^{2}L}{\partial {\theta }_i{\theta }_j}=\sum _{i=1}^d\sum _{j=1}^d\left(\Delta {\theta }_i\Delta {\theta }_j\frac{{\partial }^{2}L}{\partial {\theta }_i{\theta }_j}\right)（5）$$
这一步其实就是将向量矩阵相乘的形式展开，即可得到上式的形式。

再利用公式（3）的推导，将公式（3）带入公式（5），上述式子可以继续推导为：
$$\begin{array}{rl}\Delta {\theta }^{\top }{\mathbf{H}}^{(\theta )}\Delta \theta & =\sum _{i=1}^d\sum _{j=1}^d\Delta {\theta }_i\Delta {\theta }_j\left(\sum _{k=1}^m\sum _{l=1}^m\frac{\partial {\mathbf{z}}_k^{(n)}}{\partial {\theta }_i}\frac{{\partial }^{2}L}{\partial {\mathbf{z}}_k^{(n)}{\mathbf{z}}_l^{(n)}}\frac{\partial {\mathbf{z}}_l^{(n)}}{\partial {\theta }_j}\right)\\ & =\sum _{i=1}^d\sum _{j=1}^d\sum _{k=1}^m\sum _{l=1}^m\left(\Delta {\theta }_i\Delta {\theta }_j\frac{\partial {\mathbf{z}}_k^{(n)}}{\partial {\theta }_i}\frac{{\partial }^{2}L}{\partial {\mathbf{z}}_k^{(n)}{\mathbf{z}}_l^{(n)}}\frac{\partial {\mathbf{z}}_l^{(n)}}{\partial {\theta }_j}\right)\\ & =\sum _{k=1}^m\sum _{l=1}^m\left(\frac{{\partial }^{2}L}{\partial {\mathbf{z}}_k^{(n)}{\mathbf{z}}_l^{(n)}}\right)\left(\sum _{i=1}^d\Delta {\theta }_i\frac{\partial {\mathbf{z}}_k^{(n)}}{\partial {\theta }_i}\right)\left(\sum _{j=1}^d\Delta {\theta }_j\frac{\partial {\mathbf{z}}_l^{(n)}}{\partial {\theta }_j}\right)\\ & ={\left(\mathbf{J}\left[\frac{{\mathbf{z}}^{(n)}}{\theta }\right]\Delta \theta \right)}^{\top }{\mathbf{H}}^{\left({\mathbf{z}}^{(n)}\right)}\left(\mathbf{J}\left[\frac{{\mathbf{z}}^{(n)}}{\theta }\right]\Delta \theta \right)\end{array}（6）$$
其中，$\mathbf{J}\left[\frac{x}{y}\right]$ 表示x关于y的雅各比矩阵。
上述公式的最后一步就是将展开式以矩阵的形式表示。

还没完，还可以继续推导：
对网络输出${\mathbf{z}}^{(n)}$也进行一次泰勒展开的话，那么可以得到下式：
$$\Delta {\mathbf{z}}^{(n)}={\hat{\mathbf{z}}}^{(n)}-{\mathbf{z}}^{(n)}\approx {\mathbf{J}}_{{\mathbf{z}}^{(n)}}(\theta )\Delta \theta （7）$$
这里其实就是只保留了一阶项。

所以，最终就可以得到：
$$\begin{array}{rl}\Delta {\theta }^{\top }{\mathbf{H}}^{(\theta )}\Delta \theta & =\Delta {\mathbf{z}}^{(n),\top }{\mathbf{H}}^{\left({\mathbf{z}}^{(n)}\right)}\Delta {\mathbf{z}}^{(n)}\end{array}（8）$$

以上是该篇论文的核心推导，也是该论文所述的原理3.1. 即将原始的关于参数$\theta$的优化问题转化为关于网络输出${\mathbf{z}}^{(n)}$的优化问题，如下：
$$\underset{\hat{\theta }}{\mathrm{argmin}}\Delta {\theta }^{\top }{\overline{\mathbf{H}}}^{(\theta )}\Delta \theta \approx \underset{\hat{\theta }}{\mathrm{argmin}}\mathbb{E}\left[\Delta {\mathbf{z}}^{(n),\top }{\mathbf{H}}^{\left({\mathbf{z}}^{(n)}\right)}\Delta {\mathbf{z}}^{(n)}\right]（9）$$

下面再来梳理一下：
对于量化问题的优化目标目前存在两种，一种是直接在参数空间进行优化，即最小化量化后参数与原始训练好的浮点参数之间误差。但是有研究表明，最小化参数空间的误差并不能带来最终量化模型的最佳的性能。所以最好使用另一个优化目标，即直接优化量化后模型的损失函数，如公式（1）所示。但是这种优化方法目前主要应用在量化感知训练的情况下，而这种情况下，必须需要足够的训练数据，足够的计算资源和足够的训练时间才能得到较好的量化结果。所以呢，这篇论文就基于泰勒展开，将公式（1）中的目标函数进行展开之后得到公式（2），又因为训练之后网络已经收敛，所以第一项可以省略，只保留第二项。但是呢，因为网络中的参数量非常多，所以参数向量的维度很大，如果直接计算参数向量的海森矩阵是一件非常耗费内存，也是一件几乎不可能的事情。所以，本文核心的推导就来了，也就是公式（6）（7）（8），将损失函数对参数向量$\theta$的海森矩阵转换为损失函数对网络输出${\mathbf{z}}^{(n)}$ 的海森矩阵，从而就可以大大降低计算海森矩阵的复杂度。

2.2 块重建

根据上一小节所述，如果直接利用整个网络的最终输出${\mathbf{z}}^{(n)}$ 来近似二阶误差实现量化重建的话，其效果是差于逐层重建的方法，主要因为重建使用的校准数据太少，只有1024，很容易导致过拟合。而为了量化重建的高效性，不能增加太多的训练数据 。如何在使用较少校准数据的前提下，提高重建的网络性能呢？
在逐层重建（基于网络每一层的输出进行重建）和基于整个网络的最终输出重建之间还存在若干重建粒度。这也就是本节提出的块重建，即将若干层组成一个块，基于块的输出进行重建。其原理跟上一节提到的基于网络最终输出${\mathbf{z}}^{(n)}$重建的原理是一样的，即如果层k到等l组成一个块，该块的权重向量表示为$\tilde{\theta }=\mathrm{vec}{\left[{\mathbf{w}}^{(k),\top },\dots ,{\mathbf{w}}^{(\ell ),\top }\right]}^{\top }$,对应的海森矩阵可以表示为$\Delta {\tilde{\theta }}^{\top }{\overline{\mathbf{H}}}^{(\tilde{\theta })}\Delta \tilde{\theta }=\mathbb{E}\left[\Delta {\mathbf{z}}^{(\ell ),\top }{\mathbf{H}}^{\left({\mathbf{z}}^{(\ell )}\right)}\Delta {\mathbf{z}}^{(\ell )}\right]$。

2.3 海森矩阵的近似

前面已经提到使用基于块的方式，这样既能考虑到块内层之间的依赖性，同时将每个块的二阶误差转化为对应的该块的输出 $\mathbb{E}\left[\Delta {\mathbf{z}}^{(\ell ),\top }{\mathbf{H}}^{\left({\mathbf{z}}^{(\ell )}\right)}\Delta {\mathbf{z}}^{(\ell )}\right]$ 。但是，要想求解，该海森矩阵${\mathbf{H}}^{\left({\mathbf{z}}^{(\ell )}\right)}$必须要先求出来。目前常用的一种方式是直接假设${\mathbf{H}}^{\left({\mathbf{z}}^{(\ell )}\right)}=c\times \mathbf{I}$，这样的话，这个二次损失函数就变成${\Vert \Delta {\mathbf{z}}^{(\ell )}\Vert }^2$，但是论文指出这种方式会损失很多有用信息。

在该论文中，使用 diagonal Fisher Information Matrix (FIM) 来近似该海森矩阵。 对于一个概率模型$p(x\mid \theta )$， FIM 定义为：
$${\overline{\mathbf{F}}}^{(\theta )}=\mathbb{E}\left[{\nabla }_{\theta }\log p_{\theta }(y\mid x){\nabla }_{\theta }\log p_{\theta }(y\mid x{)}^{\mathrm{T}}\right]=-\mathbb{E}\left[{\nabla }_{\theta }^2\log p_{\theta }(y\mid x)\right]=-{\overline{\mathbf{H}}}_{\log p(x\mid \theta )}^{(\theta )}$$
FIM 就是对数似然函数的期望海森矩阵的负值。

论文中说：当模型分布和真实数据分布匹配时，损失函数的海森矩阵就等于FIM。（不理解！！！）

激活值的FIM的对角值就等于每个元素的梯度的平方。（不理解！！！）

基于上述结论，优化目标函数可以转换为：
$$\underset{\hat{\mathbf{w}}}{\min }\mathbb{E}\left[\Delta {\mathbf{z}}^{(\ell ),\top }{\mathbf{H}}^{\left({\mathbf{z}}^{(\ell )}\right)}\Delta {\mathbf{z}}^{(\ell )}\right]=\underset{\hat{\mathbf{w}}}{\min }\mathbb{E}\left[\Delta {\mathbf{z}}^{(\ell ),\top }\mathrm{diag}\left({\left(\frac{\partial L}{\partial {\mathbf{z}}_1^{(\ell )}}\right)}^2,\dots ,{\left(\frac{\partial L}{\partial {\mathbf{z}}_a^{(\ell )}}\right)}^2\right)\Delta {\mathbf{z}}^{(\ell )}\right]（10）$$
与MSE最小化相比，上述最小化包含了平方梯度信息。如果输出具有较高的绝对梯度，那么在重建时它将得到更多的关注。

在该论文中，分别对权重和激活值都进行量化，但是对权重的量化直接采用自适应的四舍五入，而对激活值的量化的step size（delta）进行学习。

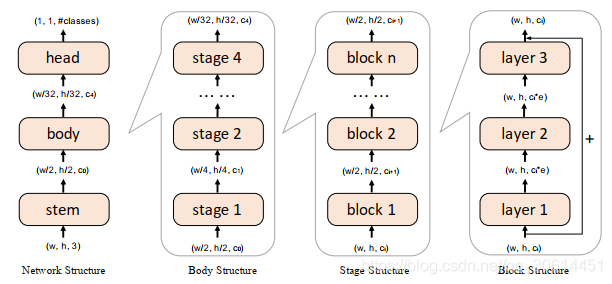
上图是该论文中提到的模型的不同的结构层次，network->body->stage->block

$$\hat{\mathbf{w}}=s\times \mathrm{clip}\left(\lfloor \frac{\mathbf{w}}{s}\rfloor +\sigma (\mathbf{v}),n,p\right)$$
上式是量化函数，不同于传统的量化函数，其额外引入了一个$\sigma (v)$函数，其中$v$是一个可学习的参数，$\sigma (\cdot )$是一个sigmoid-like的函数，使得$v$移动在0-1之间，同时再损失函数中引入一个正则化项，使得$\sigma (v)$能够收敛到0或1.
那么，最终的优化目标函数可以表示为：
$$\underset{\mathbf{v}}{\mathrm{argmin}}\mathbb{E}\left[\Delta {\mathbf{z}}^{(\ell ),\top }\mathrm{diag}\left({\left(\frac{\partial L}{\partial {\mathbf{z}}_1^{(\ell )}}\right)}^2,\dots ,{\left(\frac{\partial L}{\partial {\mathbf{z}}_a^{(\ell )}}\right)}^2\right)\Delta {\mathbf{z}}^{(\ell )}\right]+\lambda \sum _i\left(1-{\left|2\sigma \left({\mathbf{v}}_i\right)-1\right|}^{\beta }\right)$$
在校准训练过程中逐渐减小$\beta$的值，从而使得$\sigma (v)$逐渐收敛到0或1.
激活值不能使用自适应四舍五入进行量化的原因，是因为它们随不同的输入数据而变化。

2.4 混合精度

2021/5/24 10：31 添加更新；

该论文同样研究了混合混合精度量化。

所谓混合精度是指针对不同的层使用不同的量化精度（不同的比特宽度）。
该优化问题可以表述为下述优化公式：

min ⁡ c L ( w ^ , c ) ,  s.t.  H ( c ) ≤ δ , c ∈ { 2 , 4 , 8 } n . （ 11 ） \min _{\boldsymbol{c}} L(\hat{\mathbf{w}}, \mathbf{c}), \text { s.t. } H(\mathbf{c}) \leq \delta, \mathbf{c} \in\{2,4,8\}^{n} . （11） cmin​L(w^,c), s.t. H(c)≤δ,c∈{2,4,8}n.（11）

c 是长度为层数的向量，其中每个元素代表每层的比特宽度。$H(\cdot )$ 是衡量对应比特宽度下的硬件性能，该约束条件的含义是其对应的硬件性能必须满足我们设置的一个阈值条件。$\delta$ 就是设置的阈值。

该论文指出一个问题，之前的那些工作在考虑量化损失函数的时候，都是逐层计算每一层的量化损失，然后将所有层的量化损失直接相加作为总的量化损失，也就是说认为每一层在量化的时候是相互独立的，从而将混合精度的求解问题作为一个整数编程问题来求解。

但是！！！

这篇论文指出在量化时，每一层之间不能是相互独立的，它们之间应该是相互影响的。所以呢，在衡量每一层的量化损失时，应该包括两部分的损失，分别称为：对角损失和非对角损失。对角损失就是独立的衡量每一层对应的敏感度（在这篇论文里，用敏感度这个指标来指代相应的量化损失，很明显，如果一层对应的敏感度越高，那么在量化为相同的比特宽度时所产生的量化损失越大。）这个敏感度跟之前的工作做的是相同的。而非对角损失指的是不同层之间的敏感度。

很明显，这种混合精度的问题可以看作是一个搜索问题，而且搜索空间很大。为了降低搜索空间，该论文指出对于比特宽度为4和8时，量化后的精度降低很低，因此只考虑2bit的排列组合情况，从而降低搜索空间。搜索算法使用的是遗传算法。

相应的算法伪代码如下：

总结： 目前还有一些地方没弄明白，后续还需要再研究一下补充，另外，再跑一下该论文的代码，看一下实验，后续再补充！

参考文献，感谢作者。

@article{li2021brecq, title={Brecq: Pushing the limit of
post-training quantization by block reconstruction}, author={Li,
Yuhang and Gong, Ruihao and Tan, Xu and Yang, Yang and Hu, Peng and
Zhang, Qi and Yu, Fengwei and Wang, Wei and Gu, Shi}, journal={arXiv
preprint arXiv:2102.05426}, year={2021} }