梯度下降和梯度上升相关算法的分析与实现

一直在看相关的视频和书本学习机器学习的相关东西，今年就开始写第一个机器学习的博客，注重于理论分析和具体的算法的python实现，强调本博客的所有的算法均可编程实现，而不仅只是个样子(鉴于很多博客的code只是样子)....本博客专注于小白学习，大佬勿喷

好了开始，申明本博客的下面的每个算法都是基于一个项目背景的，这个的联系数据集采用的是周志华老师西瓜里的习题的数据集：

class watermenon:
    def __init__(self,number,color,root,sound,stripe,umbilical_region,touch,density,sugar_rate,quality):
        self.number=number
        self.color=color
        self.root=root
        self.sound=sound
        self.stripe=stripe
        self.umbilical_region=umbilical_region
        self.touch=touch
        self.density=density
        self.sugar_rate=sugar_rate
        self.quality=quality
        self.feature=[self.number,self.color,self.root,self.sound,self.stripe,
                      self.umbilical_region,self.touch,self.density,self.sugar_rate,self.quality]


w1 = watermenon('1', '青绿', '蜷缩', '浊响', '清晰', '凹陷', '硬滑', 0.697, 0.460, '好')
w2 = watermenon('2', '乌黑', '蜷缩', '沉闷', '清晰', '凹陷', '硬滑', 0.774, 0.367, '好')
w3 = watermenon('3', '乌黑', '蜷缩', '浊响', '清晰', '凹陷', '硬滑', 0.634, 0.264, '好')
w4 = watermenon('4', '青绿', '蜷缩', '沉闷', '清晰', '凹陷', '硬滑', 0.608, 0.318, '好')
w5 = watermenon('5', '浅白', '蜷缩', '浊响', '清晰', '凹陷', '硬滑', 0.556, 0.215, '好')
w6 = watermenon('6', '青绿', '稍蜷', '浊响', '清晰', '稍凹', '软粘', 0.403, 0.237, '好')
w7 = watermenon('7', '乌黑', '稍蜷', '浊响', '稍糊', '稍凹', '软粘', 0.481, 0.149, '好')
w8 = watermenon('8', '乌黑', '稍蜷', '浊响', '清晰', '稍凹', '硬滑', 0.437, 0.211, '好')

w9 = watermenon('9', '乌黑', '稍蜷', '沉闷', '稍糊', '稍凹', '硬滑', 0.666, 0.091, '不')
w10 = watermenon('10', '青绿', '硬挺', '清脆', '清晰', '平坦', '软粘', 0.243, 0.267, '不')
w11 = watermenon('11', '浅白', '硬挺', '清脆', '模糊', '平坦', '硬滑', 0.245, 0.057, '不')
w12 = watermenon('12', '浅白', '蜷缩', '浊响', '模糊', '平坦', '软粘', 0.343, 0.099, '不')
w13 = watermenon('13', '青绿', '稍蜷', '浊响', '稍糊', '凹陷', '硬滑', 0.639, 0.161, '不')
w14 = watermenon('14', '浅白', '稍蜷', '沉闷', '稍糊', '凹陷', '硬滑', 0.657, 0.198, '不')
w15 = watermenon('15', '乌黑', '稍蜷', '浊响', '清晰', '稍凹', '软粘', 0.360, 0.370, '不')
w16 = watermenon('16', '浅白', '蜷缩', '浊响', '模糊', '平坦', '硬滑', 0.593, 0.042, '不')
w17 = watermenon('17', '青绿', '蜷缩', '沉闷', '稍糊', '稍凹', '硬滑', 0.719, 0.103, '不')

本次练习主要就是根据密度（density）,含糖率（sugar_rate），质量（quality）来划分西瓜数据集

一：梯度下降算法

推导：给定数据集D={(x1,y1),(x2,y2),(x3,y3)...(xm,ym)},线型回归试图学得一个模型尽可能的预测给定x所对应的y值。

针对于单个样本进行推导

     （x表示样本的特征，theta表示特征对应的系统）

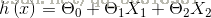
一个标准的线型多元线型函数的形式就是这样（为了方便公式中只使用了三个参数，两个特征）

在上述公式中其实theta0的特征可看为1,所以公式可以写成下面的形式：

     

根据最小二乘法可以确定对应特征函数的损失函数，另损失函数最小化，就是梯度下降法的核心思想

对该函数进行求到可以得到如下：

求导数的过程什么简单X_i代表第i的参数的对应的特征X的值，随意再求theta值的最小化过程中可以得到theta的更新规则

alhpa代表着算法的学习速度，后面的就是theta的导数，可以看成斜率，而alpha就是x的增量，总的来说就是函数的增量，如果alpha的数值过大，会导致学习过程中发生震荡难以收敛到局部最小值，如果a太小也会导致学习时间太长。推广到矩阵的形式就如下：

其中下表j代表第j个样本，i指具体某个样本的第i个特征

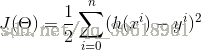
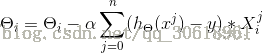
到此推导完成，下面就是代码的实现了（python）:

回顾实验目的：“根据密度（density）,含糖率（sugar_rate），质量（quality）来划分西瓜数据集”：

先自行准备数据，所使用的格式都是矩阵的格式：参考如下：

dataset=np.ones((17,3))
result=np.ones((17,1),dtype=np.uint8)
for i in range(result.shape[0]):
    if i<8:
        result[i][0] =1
    else:
        result[i][0]=0

for i in range(17):
    dataset[i][0] = wm.watermenon_data[i].feature[7]
    dataset[i][1] = wm.watermenon_data[i].feature[8]

如图所示特征空间是一个17*3的矩阵，3：的最后一个就是x0就是theta0所对应的特征，为了便于矩阵计算，写成如上形式

由于本实验的标签类型是0,1的类型，所以采用sigmoid函数（因为具体的计算结果是连续的值，需要将连续的转化成0.1离散的空间）：

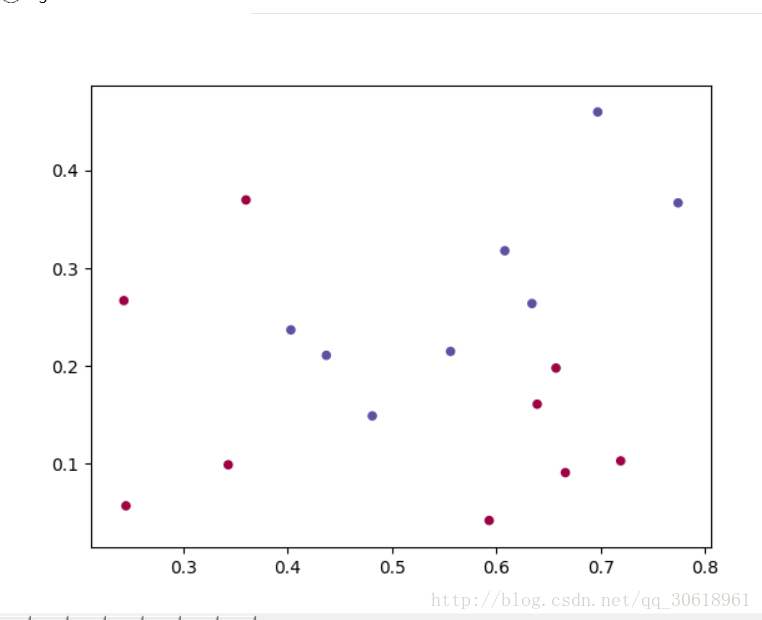
sigmoid矩阵的写法如下：不知道sigmoid函数的小白可以自己百度一下：使用matplotlib库将数据点画出来，如下：

def sigmoid(x):
    return 1/(1+np.exp(-x))

函数如下：

plt.figure()
plt.scatter(dataset[:,0], dataset[:,1], s=20, c=result, cmap=plt.cm.Spectral)
plt.show()

编写梯度下降算法：

def logistic_regression(input_matrix,label_matrix):
    alpha = 0.001   #学习速度
    maxCycles = 10000 #迭代最多的次数
    m,n=np.shape(input_matrix)
    weights=np.ones((n,1)) #初始值是1
    for k in range(maxCycles):
        h=sigmoid(np.dot(input_matrix,weights))
        error=(h-label_matrix)#梯度上升法和梯度下降法的区别在于此
        weights=weights-alpha*np.dot(np.transpose(input_matrix),error)
    return weights

weight=logistic_regression(dataset,result)

print(weight)#可以打印出权值

完成之后我们就可以得到权值theta1,theta2,theta0(写法是因为我的特征空间的x的最后一列全是1对应的theta0)：

该函数可以简单的将假设函数图形表示出来

def draw(weight):
    x=np.arange(0,1,0.01)
    y=(-weight[2][0]-weight[0][0]*x)/weight[1][0]
    plt.scatter(x,y,s=1,c='black')

记得结尾加上一句：

plt.show()

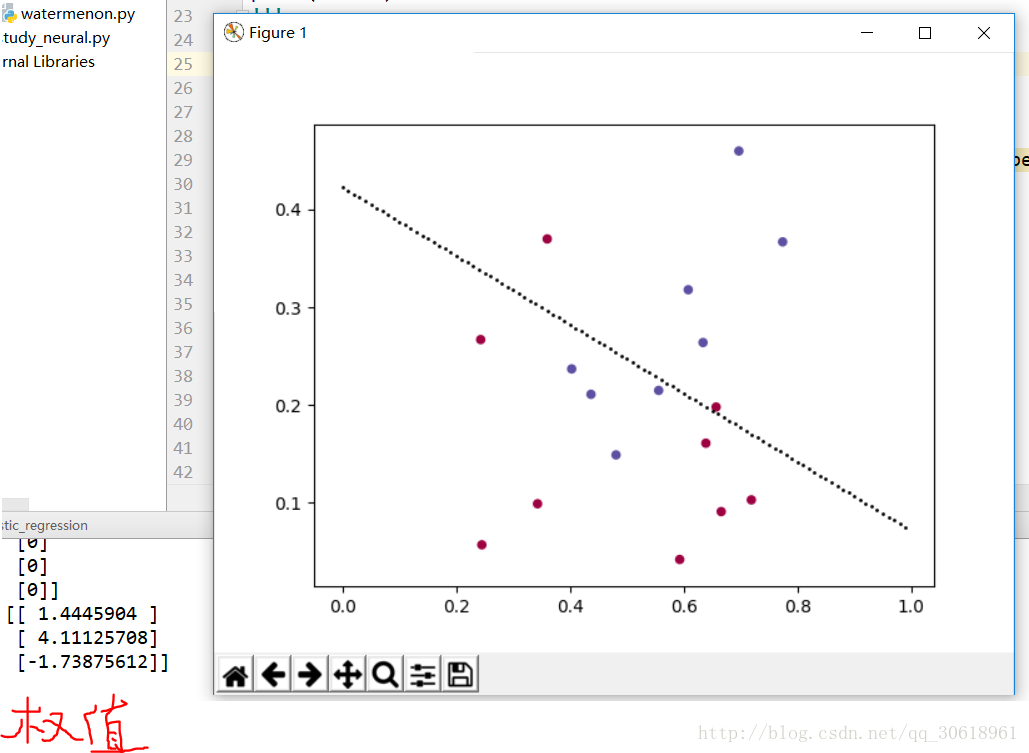
完事这就是梯度下降法的具体实现

二：梯度上升法：梯度上升法的思想是通过最大化似然函数来实现的，这边就不多讲，主要说明程序转化为梯度上升法的时候需要修改的地方，其实梯度上升和下降并无太大区别：

error=(h-label_matrix)#梯度上升法和梯度下降法的区别在于此
#error=(label_matrix-h)
weights=weights-alpha*np.dot(np.transpose(input_matrix),error)
#weights=weights+alpha*np.dot(np.transpose(input_matrix),error)

ok...................

转载请标明出处（：|）