【电赛笔记】PID控制算法原理及代码仿真

PID算法是什么、能干什么以及为什么要用PID算法

PID算法是一个闭环控制（有反馈）算法，利用它可以让要控制的量快速、准确地到达目标值。相比于PID算法，常用的开环控制（无反馈）算法不能及时发现干扰的存在并修正。下面我们分析一下各个部分的作用。
以下分析均以控制无人机悬停为例（g取9.8，不考虑空气阻力）。

公式分析

$$out(t)=K_p\cdot err(t)+K_i\cdot {\int }_0^{t}err(t)dt+K_d\cdot \frac{err(t)-err(t-dt)}{dt}$$
PID的公式有三个部分组成：比例控制部分（P）、积分控制部分（I）和微分控制部分（D），其中$K_i、K_p、K_d$分别是这三个部分的系数。

比例控制

当把Ki与Kd均置零，Kp设置为1，目标设置为100，初始值设为0时，高度、速度和推力随时间的曲线图如下。显然，在只有比例控制的情况下，高度会迅速达到并超过目标值，然后再迅速下降回到起点（这种越过目标然后返回的现象被称为过冲），如此往复，震荡幅度非常大。这肯定不是我们需要的。

注意观察速度曲线，只有高度超过目标值以后速度才开始下降，而物体是存在惯性的，如果减速过晚，那物体势必会因为惯性冲过目标位置。那么我们现在只需要让物体速度受到一定的限制，不要无限制的增长就行了。也就是我们需要一个与速度的相反数成正相关的量来约束物体的速度。
物理学和数学告诉我们速度其实是位移对时间的微分，即
$$v=\frac{dx}{dt}=\frac{x_t-x_{t-1}}{\Delta t}$$

微分控制

那么，在这个例子中，只要把x换成err或者是h然后前面添加一个负号就可以了。现在我把微分控制的系数Ki分别设置为1、3、5、10，于是曲线变成了下面这个样子。

我们发现，随着微分项系数不断增大，速度的变化率，也就是加速度越来越小，而且曲线振荡的幅度也越来越小，直到完全不存在振荡。
再仔细观察一下，我们发现在振荡被抑制后，曲线最终收敛到了震荡的平衡位置，而这个位置仅仅是我们目标位置的二分之一，这是完全不可以接受的！而且这时候误差值err并不为0，难道比例控制部分没有发挥作用吗？
注：这种曲线达到平稳后存在的误差叫做稳态误差。
我把比例控制系数Kp调整为原来的10倍，也就是现在的参数为$K_p=10,K_d=1$，曲线如下。

可以发现，情况确实好转了不少，起码最终可以稳定在目标值附近了。但是如果我们用标尺测量曲线稳定后的值就会发现，误差仍然存在，如下图。而当我把Kp增加至100时，这个小小的误差终于几乎消失了。

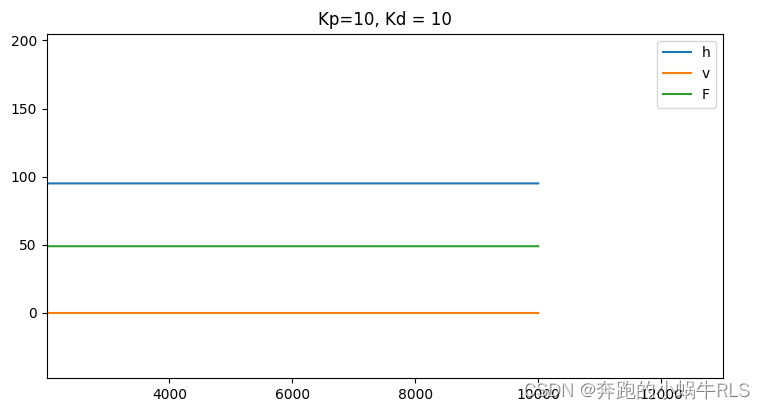
但是通过增大Kp值来解决这个误差显然不是一个好主意，因为增大Kp意味着在目标值变大后过冲又会变严重，而抑制过冲又需要增大Kd值，但增大Kd又会引入稳态误差，就跟和面时“面多加水、水多加面”一样，最终Kp和Kd都会变得很大，而且与目标值相关。

积分控制

在添加微分控制之前，虽然存在过冲和严重的振荡，但是被控量是可以达到目标值的，而添加微分控制以后，过冲和振荡消失了，但是被控量却达不到目标值了。
我们对物体进行一下受力分析，物体受两个力，一个是自身的重力，一个是向上的推力。而这个推力与物体当前位置到目标位置的距离成比例。那么必然存在一个位置，在这个位置，物体受到的推力和重力平衡。在这个位置之前，合力向上，物体加速上升；这个位置之后，物体开始减速，然后向下加速运动。但是一旦恰好在这个平衡位置速度为0的话，那就会停在这个位置了。而在比例控制和微分控制的共同作用下，最终就是这种情况。

PID中的积分控制项就是用来解决稳态误差的。这一项会让稳态误差随着时间积累，并最终作用到控制量上。一般情况下，积分项的系数去一个非常小的值，比如0.05就可以了。为了防止积分值无限制地增大，我们一般还会设置一个积分项最大值。
这里我把积分项系数分别设为0.03、0.05和0.07，如下图。

从图中可以看出，积分项系数越大，曲线达到稳态的速度越快。注意左下角的第三张图，当积分项系数达到0.07时，曲线出现了一个小小的过冲，而当适当减小微分项系数后，这个过冲便消失了。
现在第四张图便是一个比较完美的PID控制曲线。不过这个曲线只适用于目标高度为100的情形，并没有很强的适应性，还需要调整参数来让它具备适应各种高度的能力。

仿真代码

import matplotlib.pyplot as plt

class PIDController:
    def __init__(self, p, i, d, start, aim) -> None:
        
        # 常量
        self.dt = 0.05 	# 物理过程的时间间隔，单位：s
        self.m = 5 		# 物体的质量，单位：kg
        self.g = 9.8 	# 重力加速度：m/s^2
        self.f_max = 200 # 最大推力，单位：N
        self.i_max = 200
        # 状态变量
        self.Kp = p		# 比例系数
        self.Ki = i	# 积分系数
        self.I = 0  # 积分项
        self.Kd = d		# 微分系数
        self.h = start		# 当前高度，单位：m
        self.h_aim = aim	# 目标高度，单位：m
        self.v = 0		# 当前速度
        self.a = 0		# 当前加速度

        self.list_h = []	# 高度
        self.list_v = []	# 速度
        self.list_f = [] # 推力

    def run(self):

        ticks = 10000	# 仿真多少个dt
        last_err = 0	# 上一时刻的误差值
        for t in range(0, ticks):
            err = self.h_aim - self.h
            self.I += err*self.dt
            i = self.Ki * self.I
            # 限制一下积分项的范围
            if i > self.i_max:
                i = self.i_max
            if i < 0:
                i = 0
            F = self.Kp*err + self.Ki*self.I + self.Kd*(err-last_err)/self.dt
            # 限制推力的范围
            if F > self.f_max:
                F = self.f_max
            if F < 0:
                F = 0
            last_err = err
            # 物理仿真
            self.a = -self.g + F/self.m
            self.v += self.a * self.dt
            self.h += self.v * self.dt
            # 保存状态变量
            self.list_h.append(self.h)
            self.list_v.append(self.v)
            self.list_f.append(F)
        return (self.list_h, self.list_v, self.list_f)

time = range(0, 10000)
# p i d start aim
pids = [
    (3, 0.010, 18, 0, 100),
    (3, 0.010, 18, 0, 200),
    (3, 0.010, 3, 0, 400),
    (3, 0.010, 18, 0, 20)
]
for i, d in enumerate(pids):
    pid = PIDController(*d)
    plt.subplot(2, 2, i+1)
    plt.title("p=%.2f,i=%.2f d=%.2f,aim=%.2f" % (d[0], d[1], d[2], d[4]))
    lists = pid.run()
    plt.plot(time, lists[0], label="h")
    plt.plot(time, lists[1], label="v")
    plt.plot(time, lists[2], label="F")
    plt.legend()
plt.show()