动态规划之钢条切割问题

欢迎关注，定期更新算法问题！

这一篇来讨论一下关于动态规划的一些问题。

动态规划和分治方法类似，都是组合子问题的解来求解原问题，但是两者不同的是分治方法将问题化为互不相交的子问题，递归的求解子问题，再将子问题的解组合起来求解原问题；而动态规划应用于子问题重叠的情况，即不同的子问题有公共的子子问题。所以在这种情况下，分治方法会重复计算那些公共子问题，但是动态规划对公共子问题只求解一次。

动态规划通常来求解最优化问题，这类问题通常有多个可行解，我们希望寻找最优解，我们称这样的解为一个最优解，因为问题可能有多个最优解。我们通常按照下面4个步骤来设计算法：

（1）、刻画一个最优解的结构特征；

（2）、递归的定义最优解的值；

（3）、计算最优解的值，通常采用自底向上的方法；

（4）、利用计算出的信息构造一个最优解。

先来看第一个例子：钢条切割问题

问题简述：某公司购买长钢条，希望将长钢条切割成短钢条出售，已知切割工序不耗费费用，下表给出了价格与长度的一个对应关系，现在希望得到一个最优的切割方案。

长度为n的钢条有2^(n-1)种切割方案，因为在距离钢条左端距离为i处，我们要么切割要么不切割，只有两种方案。假设最优切割方案为k段，那么最大的收益就是这k段效益的和。

为了求解原问题，首先求解形式相近，规模更小的子问题，即首次切割将长度为n的钢条切割成长度为i和n-i的钢条，再将这两个钢条看成相互独立的问题切割，我们通过组合两个问题的最优解，选取效益最大的构成原问题的解，这样可以认为此问题满足最优子结构性质：即原问题的最优解可以由子问题的最优解组成，而子问题可以独立求解。

用上述思想求解，其实子问题是划分为左、右两部分进行的，当然可以有一种简化的方法，即子问题只从右部分划分进行，思路就是：将长度为n的钢条划分为长度为i的左部分和长度n-i的右部分，左半部分不在划分，只是将右半部分继续划分。

下边给出这种朴素递归方法的实现：

DataType Cut_Rod(DataType p[],int n)
{
    if(n==0)
        return 0;
    DataType q=0;
    for(int i=0;i<n;i++)
        q=max(q,p[i]+Cut_Rod(p,n-i-1));
    return q;
}

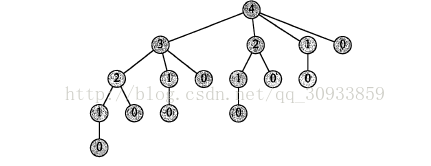
此程序可以正确的求解问题的解，但问题是随着数据的增大，运行时间会爆炸性的增长，原因就是程序重复的计算相同的子问题，可以看下图这个树结构理解：

上述递归树结点的标号表示问题的规模，，根结点到子结点的边表示切割方案，由于此算法是由顶到底的递归，故此重复的计算了大量相同的子问题，可以证明花费的时间为2的n次方幂，这个运行时间是相当恐怖的，下边我们考虑更高效的动态规划算法。设计算法时可以考虑合理安排子问题顺序，使得子问题只求解一次，并且将子问题的解保存下来，等到后边用到时再利用，相比原来算法只是花了更多的内存，其实就是用空间换时间的思想。

有两种实现方式：

（1）、带备忘的自顶向下递归法：此方法和上述朴素方法递归方向是一样的，但是区别就是会保存子问题的解，当计算子问题时首先查看是否计算过此问题，如果计算过，则直接利用，否则，用常规方法计算。

//带备忘的自顶向下递归
DataType Cut_Rod_upTodown(DataType p[],int n,DataType Subvalue[])
{
    if(n==0)
        return 0;
    DataType q=0;
    for(int i=0;i<n;i++)
    {
        if(Subvalue[n-i-1]==0)
        {
            q=max(q,p[i]+Cut_Rod_upTodown(p,n-i-1,Subvalue));
        }
        else
        {
            q=max(q,p[i]+Subvalue[n-i-1]);
        }
    }
    return q;
}

如果你的编译器是gcc等，会可以直观的看到运行时间的差别。

（2）、自底向上递归法：仔细看上边的朴素算法递归树，自顶向下的递归可以看成树从左半部分开始递归，但是我们考虑让其从右半部分递归，即对子问题的求解依赖于规模更小的子问题的求解，我们可以把问题的规模从小到大排序，这样程序的求解从更小的子问题开始，然后再去计算较大的子问题，这样每个子问题只计算一遍。

//自底向上的算法
DataType Cut_Rod_downToup(DataType p[],int n)
{
    DataType value[5]={0};
    for(int i=1;i<=n;i++)
    {
        DataType q=0;
        for(int j=1;j<=i;j++)
        {
            q=max(q,p[j]+value[i-j]);
        }
        value[i]=q;
    }
    return value[n];
}

上述算法两层循环，思路就是当计算规模为i的收益时，计算规模比i小的子问题的最优解，即第二层循环，可以简单的理解成从小到大一直都是最优的话，最终就是最优的。

上述三个算法解决了输出效益的问题，但是如何输出划分方案呢？下边进行一次重构解，将结果输出：

//重构输出解
void print_Cut_Rod_downToup(DataType p[],int n,DataType value[],int result[])
{
    for(int i=1;i<=n;i++)
    {
        DataType q=0;
        for(int j=1;j<=i;j++)
        {
            if(q<(p[j]+value[i-j]))
            {
                q=p[j]+value[i-j];
                result[i]=j;
            }
        }
        value[i]=q;
    }
}

结果保留在result中

好了，这篇文章到此结束。

最后附上全部测试代码：（注意测试代码给出的问题的规模为4）

#include <iostream>
typedef int DataType;
using namespace std;
//朴素递归算法
DataType Cut_Rod(DataType p[],int n)
{
    if(n==0)
        return 0;
    DataType q=0;
    for(int i=0;i<n;i++)
        q=max(q,p[i]+Cut_Rod(p,n-i-1));
    return q;
}
//带备忘的自顶向下递归
DataType Cut_Rod_upTodown(DataType p[],int n,DataType Subvalue[])
{
    if(n==0)
        return 0;
    DataType q=0;
    for(int i=0;i<n;i++)
    {
        if(Subvalue[n-i-1]==0)
        {
            q=max(q,p[i]+Cut_Rod_upTodown(p,n-i-1,Subvalue));
        }
        else
        {
            q=max(q,p[i]+Subvalue[n-i-1]);
        }
    }
    return q;
}
//自底向上的算法
DataType Cut_Rod_downToup(DataType p[],int n)
{
    DataType value[5]={0};
    for(int i=1;i<=n;i++)
    {
        DataType q=0;
        for(int j=1;j<=i;j++)
        {
            q=max(q,p[j]+value[i-j]);
        }
        value[i]=q;
    }
    return value[n];
}
//重构输出解
void print_Cut_Rod_downToup(DataType p[],int n,DataType value[],int result[])
{
    for(int i=1;i<=n;i++)
    {
        DataType q=0;
        for(int j=1;j<=i;j++)
        {
            if(q<(p[j]+value[i-j]))
            {
                q=p[j]+value[i-j];
                result[i]=j;
            }
        }
        value[i]=q;
    }
}
int main()
{
    DataType p[10]={1,5,8,9,10,17,17,20,24,30};
    //p1是算法三的效益测试值，由于算法的特殊性，故此第一项是0
    DataType p1[11]={0,1,5,8,9,10,17,17,20,24,30};
    DataType Subvalue[4]={0};
    DataType value[5]={0};
    int result[5]={0};
    int n=4;
    DataType Got1=Cut_Rod(p,n);
    DataType Got2=Cut_Rod_upTodown(p,n,Subvalue);
    DataType Got3=Cut_Rod_downToup(p1,n);
    print_Cut_Rod_downToup(p1,n,value,result);
    cout<<"长度为4的钢条最大收益："<<"第一种："<<Got1<<endl<<"第二种："<<Got2<<endl<<"第三种："<<Got3<<endl;
    cout<<"解的长度："<<endl;
    for(int i=0;i<=n;i++)
        cout<<result[i]<<endl;
    return 0;
}