算法（一） --DP动态规划（LIS和LCS）

1.http://blog.csdn.net/u013445530/article/details/45645307

DP问题是ACM里面最难的，因为太考思维能力了，只有将状态转移方程推出来才能解决问题，DP问题也是面试的时候最容易考到的，希望大家好好学DP，至少在面试的时候不吃亏。

1. 第一个问题

d(i)=min{ d(i-vj)+1 }   状态转移方程 其中i-vj >=0，vj表示第j个硬币的面值;

d(i)=j来表示凑够i元最少需要j个硬币

1. int main()      //代码求解的是一个数值 最少由多少个硬币组成。
2. {  
3.     int a[3] = {1,3,5},sum = 11,cent = 0,dp[12];  
4.     dp[0] = 0;  
5.     for(int i = 1; i <= sum; i++) dp[i] = i;//我们假设存在1元的硬币那么i元最多只需要i枚1元硬币，当然最好设置dp[i]等于无穷大  
6.                                             //dp[i]=i 是代表 最多的话需要i个一元硬币
7.     for(int i = 1; i <= sum; i++){      / /i代表数值
8.         for(int j = 0; j < 3; j++){     //j代表总共的硬币种类数目    i代表要求和的数
9.             if(i >= a[j] && dp[i - a[j]] + 1 < dp[i]){     //如果i的数值大于A【j】里面的数 （即数值大于硬币代表的数）
10.                 dp[i] = dp[i- a[j] ] + 1;                //注意这个是从小的数值往大的数值上 增加。 
11.             }                //所以 如果i的数值大于A【j】里面的数 以及dp[i - a[j]] + 1   选个硬币值a【j】所以要加1 
12.         }  
13.     }  
14.     cout<<dp[sum]<<endl;  
15.     return 0;  
16. }  

  

第二个问题

将一个由N行数字组成的三角形，如图所以，设计一个算法，计算出三角形的由顶至底的一条路径，使该路径经过的数字总和最大。

好了，现在我们用DP解决这道问题

 

将上图转化一下：

假设上图用map[][]数组保存。

令f[i][j]表示从顶点(1, 1)到顶点(i, j)的最大值。

则可以得到状态转移方程：

f[i][j] = max(f[i+1][j], f[i+1][j+1]) + map[i][j]

此题既适合自顶而下的方法做，也适合自底而上的方法，

当用自顶而下的方法做时，最后要在在最后一列数中找出最大值，

而用自底而上的方法做时，f[1][1]即为最大值。

所以我们将图2根据状态转移方程可以得到图3：

    这里用的是从底端向上计算

最大值是30.

代码如下:

1. 1 #include <cstdio>    
2. 2. #include <iostream>    
3. 3. #include <algorithm>    
4. 4. #include <cstring>    
5. 5. using namespace std;    
6. 6. int a[2000][2000];    
7. 7. int main()    
8. 8. {    
9. 9.     int t,n,i,j;    
10. 10.     while(~scanf("%d",&n))         
11. 11.     {   
12. 12.         for(i=0; i<n; i++)    
13. 13.             for(j=0; j<=i; j++)    
14. 14.                 scanf("%d",&a[i][j]);       //先把数存进去
15. 15.         for(i=n-1; i>0; i--)        //因为是从底部往上面求 所以i从n-1 开始  从倒数第二行开始算起
16. 16.             for(j=0; j<i; j++)       //注意这里j的范围  j从每行的第一个数算起  算到每行最后一个数，最后一个数比i小1
17. 17.                 a[i-1][j]+=max(a[i][j],a[i][j+1]);     // 让此位置的值加上 下面两个最大的值 即为最大
18. 18.         printf("%d\n",a[0][0]);    
19. 19.     }    
20. 20.     return 0;    
21. 21. }    

问题三

一个序列有N个数：A[1],A[2],…,A[N]，求出最长非降子序列的长度。 (讲DP基本都会讲到的一个问题LIS：longest increasing subsequence)

正如上面我们讲的，面对这样一个问题，我们首先要定义一个“状态”来代表它的子问题，并且找到它的解。注意，大部分情况下，某个状态只与它前面出现的状态有关，而独立于后面的状态。

让我们沿用“入门”一节里那道简单题的思路来一步步找到“状态”和“状态转移方程”。假如我们考虑求A[1],A[2],…,A[i]的最长非降子序列的长度，其中i<N，那么上面的问题变成了原问题的一个子问题(问题规模变小了，你可以让i=1,2,3等来分析) 然后我们定义d(i)，表示前i个数中以A[i]结尾的最长非降子序列的长度。OK，对照“入门”中的简单题，你应该可以估计到这个d(i)就是我们要找的状态。如果我们把d(1)到d(N)都计算出来，那么最终我们要找的答案就是这里面最大的那个。状态找到了，下一步找出状态转移方程。

为了方便理解我们是如何找到状态转移方程的，我先把下面的例子提到前面来讲。如果我们要求的这N个数的序列是：

5，3，4，8，6，7

根据上面找到的状态，我们可以得到：（下文的最长非降子序列都用LIS表示）

· 前1个数的LIS长度d(1)=1(序列：5)

· 前2个数的LIS长度d(2)=1(序列：3；3前面没有比3小的)

· 前3个数的LIS长度d(3)=2(序列：3，4；4前面有个比它小的3，所以d(3)=d(2)+1)

· 前4个数的LIS长度d(4)=3(序列：3，4，8；8前面比它小的有3个数，所以 d(4)=max{d(1),d(2),d(3)}+1=3)

OK，分析到这，我觉得状态转移方程已经很明显了，如果我们已经求出了d(1)到d(i-1)，那么d(i)可以用下面的状态转移方程得到：

d(i) = max{1, d(j)+1},其中j<i,A[j]<=A[i]

用大白话解释就是，想要求d(i)，就把i前面的各个子序列中，最后一个数不大于A[i]的序列长度加1，然后取出最大的长度即为d(i)。当然了，有可能i前面的各个子序列中最后一个数都大于A[i]，那么d(i)=1，即它自身成为一个长度为1的子序列。

分析完了，上图：(第二列表示前i个数中LIS的长度，第三列表示，LIS中到达当前这个数的上一个数的下标，根据这个可以求出LIS序列)

 

代码:

1. #include <cstdio>    

2. #include <iostream>    
3. #include <algorithm>    
4. #include <cstring>    
5. usingnamespace std;    
6.      
7. int main()    //最长非降子序列的长度
8. {    
9.     int dp[2000],a[2000],n;    
10.     while(cin>>n)    
11.     {    
12.         memset(dp,0,sizeof(dp));    
13.         int res = 0;    
14.         for(inti = 0; i < n; i++) cin>>a[i];    //先存入序列
15.      
16.         for(int i = 0; i < n; i++)    
17.         {                                                  //循环是从第一个数值开始往后求 dp[i] 
18.             dp[i] = 1;              // 先假设所有的 最长为1    即为其本身  eg：用3 5 4 去想一遍流程
19.             for(int j = 0; j < i; j++)    //j小于i   j为i前面的一个数据
20.             {    
21.                 if(a[j] < a[i])  //因为求的是最长非降子序列 LIS，即序列往后只能增加数  

                                                            //这里每次都从0开始 遍历   保证dp[i]为最长的
22.                 dp[i] = max(dp[i],dp[j] + 1); //   求出的序列 前面的数只能小于或者等于后面的数
23.             }    
24.      
25.           res = max(res,dp[i]);      //res存放每次 算出来的最大 dp[i]
26.         }    
27.      
28.         cout<<res<<endl;    
29.     }    
30.     return0;    
31. }  

问题四

最长上升公共子序列问题: LCS  （最长公共子序列） 只要两个字符串里面都有 即可。数字不必相邻

问题描述

    什么是最长公共子序列呢?好比一个数列S，如果分别是两个或多个已知数列的子序列，且是所有符合此条件序列中最长的，则S 称为已知序列的最长公共子序列。

    举个例子，如：有两条随机序列，如 1 3 4 5 5 ，and 2 4 5 6 5 7 6，则它们的最长公共子序列便是：4 5 5。

LCS问题的解决思路

动态规划算法

    事实上，最长公共子序列问题也有最优子结构性质。

记:

Xi=﹤x1，⋯，xi﹥即X序列的前i个字符 (1≤i≤m)（前缀）

Yj=﹤y1，⋯，yj﹥即Y序列的前j个字符 (1≤j≤n)（前缀）

假定Z=﹤z1，⋯，zk﹥∈LCS(X , Y)。

· 

若xm=yn（最后一个字符相同），则不难用反证法证明：该字符必是X与Y的任一最长公共子序列Z（设长度为k）的最后一个字符，即有zk = xm = yn 且显然有Zk-1∈LCS(Xm-1 , Yn-1)即Z的前缀Zk-1是Xm-1与Yn-1的最长公共子序列。此时，问题化归成求Xm-1与Yn-1的LCS（LCS(X , Y)的长度等于LCS(Xm-1 , Yn-1)的长度加1）。

· 

· 

若xm≠yn，则亦不难用反证法证明：要么Z∈LCS(Xm-1, Y)，要么Z∈LCS(X , Yn-1)。由于zk≠xm与zk≠yn其中至少有一个必成立，若zk≠xm则有Z∈LCS(Xm-1 , Y)，类似的，若zk≠yn 则有Z∈LCS(X , Yn-1)。此时，问题化归成求Xm-1与Y的LCS及X与Yn-1的LCS。LCS(X , Y)的长度为：max{LCS(Xm-1 , Y)的长度, LCS(X , Yn-1)的长度}。

· 

    由于上述当xm≠yn的情况中，求LCS(Xm-1 , Y)的长度与LCS(X , Yn-1)的长度，这两个问题不是相互独立的：两者都需要求LCS(Xm-1，Yn-1)的长度。另外两个序列的LCS中包含了两个序列的前缀的LCS，故问题具有最优子结构性质考虑用动态规划法。

    也就是说，解决这个LCS问题，你要求三个方面的东西：1、LCS（Xm-1，Yn-1）+1；2、LCS（Xm-1，Y），LCS（X，Yn-1）；3、max{LCS（Xm-1，Y），LCS（X，Yn-1）}。

    行文至此，其实对这个LCS的动态规划解法已叙述殆尽，不过，为了成书的某种必要性，下面，我试着再多加详细阐述这个问题。

第三节、动态规划算法解LCS问题

3.1、最长公共子序列的结构

    最长公共子序列的结构有如下表示：

    设序列X=<x1, x2, …, xm>和Y=<y1, y2, …, yn>的一个最长公共子序列Z=<z1, z2, …, zk>，则：

1. 若xm=yn，则zk=xm=yn且Zk-1是Xm-1和Yn-1的最长公共子序列；

2. 若xm≠yn且zk≠xm ，则Z是Xm-1和Y的最长公共子序列；

3. 若xm≠yn且zk≠yn ，则Z是X和Yn-1的最长公共子序列。

    其中Xm-1=<x1, x2, …, xm-1>，Yn-1=<y1, y2, …, yn-1>，Zk-1=<z1, z2, …, zk-1>。

3、2.子问题的递归结构

    由最长公共子序列问题的最优子结构性质可知，要找出X=<x1, x2, …, xm>和Y=<y1, y2, …, yn>的最长公共子序列，可按以下方式递归地进行：当xm=yn时，找出Xm-1和Yn-1的最长公共子序列，然后在其尾部加上xm(=yn)即可得X和Y的一个最长公共子序列。当xm≠yn时，必须解两个子问题，即找出Xm-1和Y的一个最长公共子序列及X和Yn-1的一个最长公共子序列。这两个公共子序列中较长者即为X和Y的一个最长公共子序列。

    由此递归结构容易看到最长公共子序列问题具有子问题重叠性质。例如，在计算X和Y的最长公共子序列时，可能要计算出X和Yn-1及Xm-1和Y的最长公共子序列。而这两个子问题都包含一个公共子问题，即计算Xm-1和Yn-1的最长公共子序列。

    与矩阵连乘积最优计算次序问题类似，我们来建立子问题的最优值的递归关系。用c[i,j]记录序列Xi和Yj的最长公共子序列的长度。其中Xi=<x1, x2, …, xi>，Yj=<y1, y2, …, yj>。当i=0或j=0时，空序列是Xi和Yj的最长公共子序列，故c[i,j]=0。其他情况下，由定理可建立递归关系如下：

 

代码如下:

1. 1. #include <cstdio>    
2. 2. #include <iostream>    
3. 3. #include <algorithm>    
4. 4. #include <cstring>    
5. 5. using namespace std;    
6. 6.      
7. 7. int main()    
8. 8. {    
9. 9.     string str1,str2;    
10. 10.     int dp[200][200];    
11. 11.     while(cin>>str1>>str2)    
12. 12.     {    
13. 13.         memset(dp,0,sizeof(dp));    
14. 14.      
15. 15.         int la = str1.length();    //字符串的长度
16. 16.         int lb = str2.length();    
17. 17.      
18. 18.         for(int i = 1; i <= la; i++)    
19. 19.             for(int j = 1; j <= lb; j++)    
20. 20.         {    
21. 21.             if(str1[i - 1] == str2[j - 1])       如果最后一个字母相同（这里str1[i - 1] 代表最后一个字母）
22. 22.             {    
23. 23.                 dp[i][j] = dp[i-1][j-1]+1;    
24. 24.             }    
25. 25.             else dp[i][j] = max(dp[i-1][j],dp[i][j-1]);    
26. 26.         }    
27. 27.         cout<<dp[la][lb]<<endl;    
28. 28.     }    
29. 29.     return 0;  

HDU2191

HDU1159

HDU1432

HDU2084

关于LCS递归公式的补充说明

4.递归公式

        第3节说了LCS的特征，我们可以发现，假设我需要求 a1 ... am 和 b1 .. b(n-1)的LCS 和 a1 ... a(m-1) 和 b1 .. bn的LCS，一定会递归地并且重复地把如a1... a(m-1) 与 b1 ... b(n-1) 的 LCS 计算几次。所以我们需要一个数据结构来记录中间结果，避免重复计算。

        假设我们用c[i,j]表示Xi 和 Yj 的LCS的长度（直接保存最长公共子序列的中间结果不现实，需要先借助LCS的长度）。其中X = {x1 ... xm}，Y ={y1...yn}，Xi = {x1 ... xi}，Yj={y1... yj}。可得递归公式如下：

         

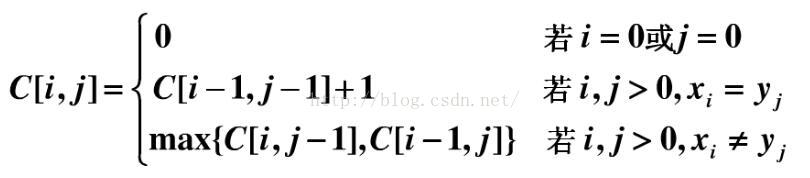
5.计算LCS的长度

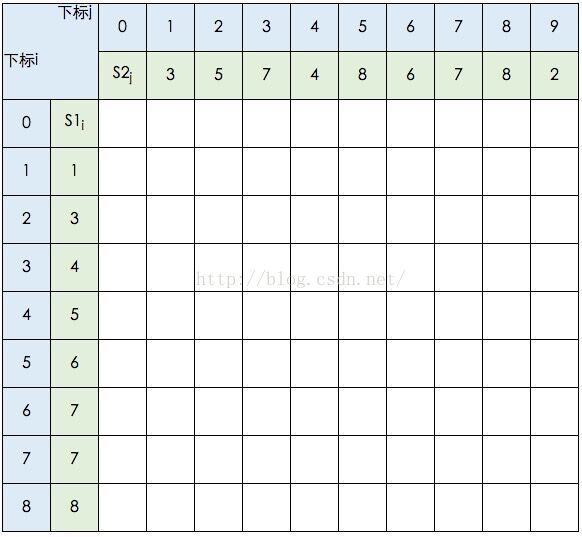
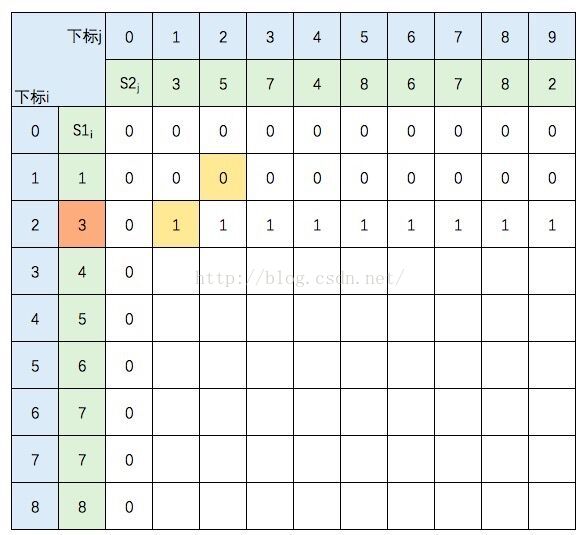
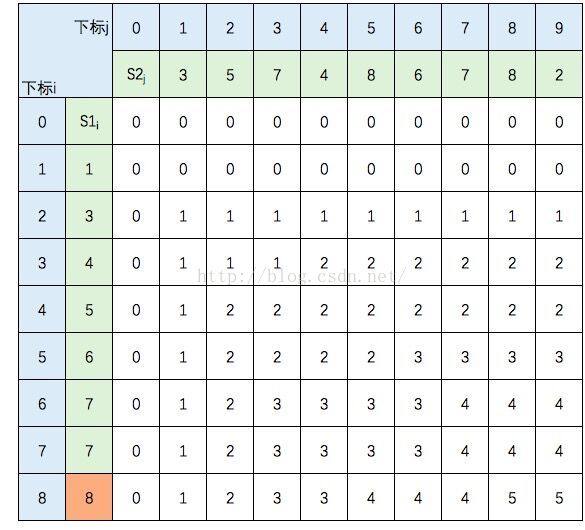
       这里我不打算贴出相应的代码，只想把这个过程说明白。还是以s1={1,3,4,5,6,7,7,8},s2={3,5,7,4,8,6,7,8,2}为例。我们借用《算法导论》中的推导图：

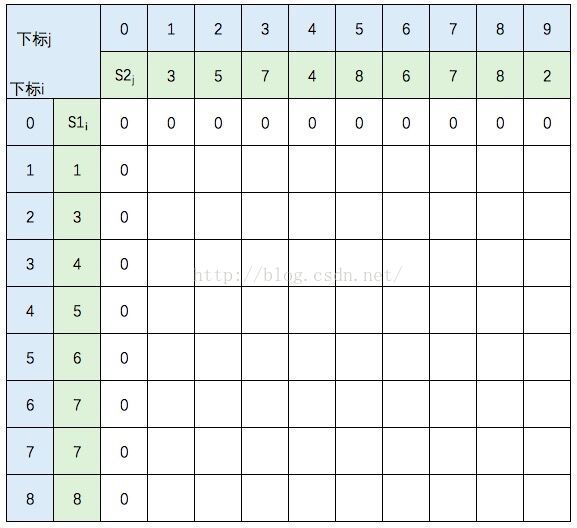
         图中的空白格子需要填上相应的数字（这个数字就是c[i,j]的定义，记录的LCS的长度值）。填的规则依据递归公式，简单来说：如果横竖（i,j）对应的两个元素相等，该格子的值 = c[i-1,j-1] + 1。如果不等，取c[i-1,j] 和 c[i,j-1]的最大值。首先初始化该表：

         

          然后，一行一行地从上往下填：

         

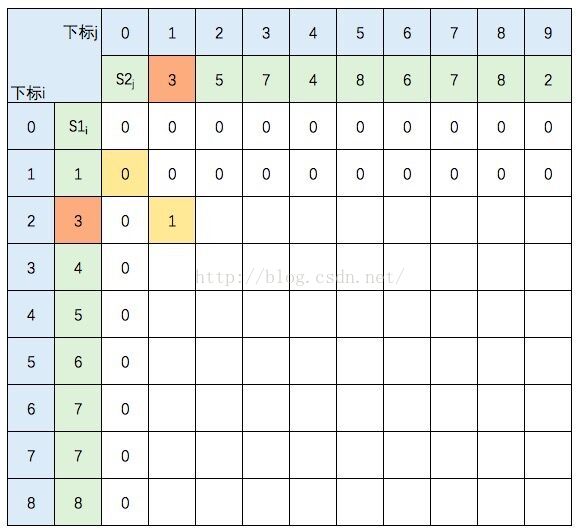
          S1的元素3 与 S2的元素3 相等，所以 c[2,1] = c[1,0] + 1。继续填充：

          

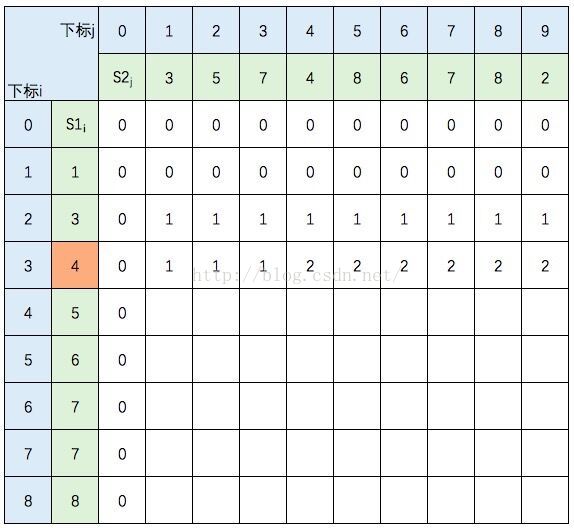
            S1的元素3 与 S2的元素5 不等，c[2,2] =max(c[1,2],c[2,1])，图中c[1,2] 和 c[2,1] 背景色为浅黄色。

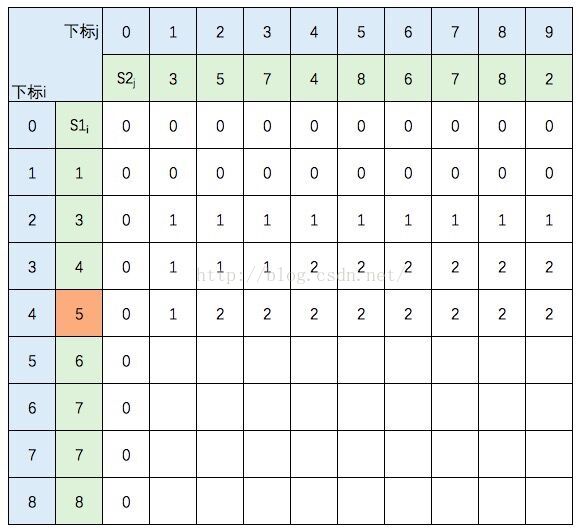
            继续填充：

            

            

             

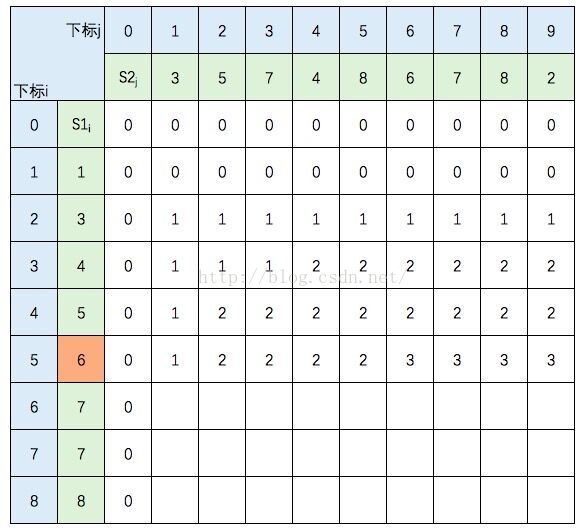
               中间几行填写规则不变，直接跳到最后一行：

              

                至此，该表填完。根据性质，c[8,9] = S1 和 S2 的 LCS的长度，即为5。

6.构造LCS

       本文S1和S2的最LCS并不是只有1个，本文并不是着重讲输出两个序列的所有LCS，只是介绍如何通过上表，输出其中一个LCS。

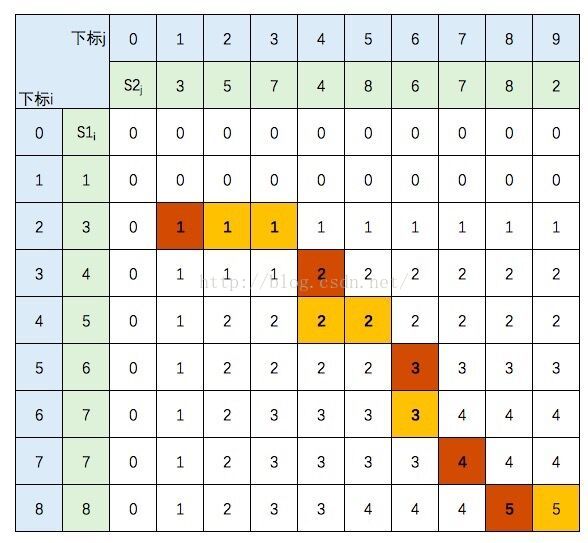
       我们根据递归公式构建了上表，我们将从最后一个元素c[8][9]倒推出S1和S2的LCS。

       c[8][9] = 5，且S1[8] != S2[9]，所以倒推回去，c[8][9]的值来源于c[8][8]的值(因为c[8][8] > c[7][9])。

       c[8][8] = 5,  且S1[8] = S2[8], 所以倒推回去，c[8][8]的值来源于 c[7][7]。

       以此类推，如果遇到S1[i] != S2[j] ，且c[i-1][j] = c[i][j-1] 这种存在分支的情况，这里请都选择一个方向（之后遇到这样的情况，也选择相同的方向）。

       第一种结果为：

       

          这就是倒推回去的路径，棕色方格为相等元素，即LCS = {3,4,6,7,8}，这是其中一个结果。

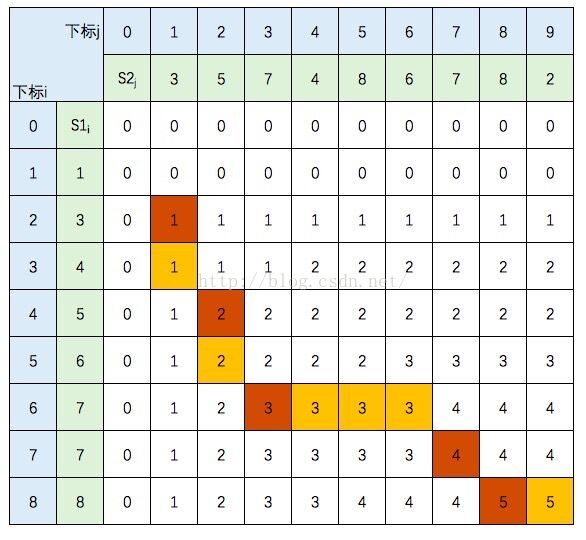
          如果如果遇到S1[i] != S2[j] ，且c[i-1][j] = c[i][j-1] 这种存在分支的情况，选择另一个方向，会得到另一个结果。

          

           即LCS ={3,5,7,7,8}。