方格填数 （搜索）

1160: 方格填数

时间限制: 1 Sec   内存限制: 128 MB
提交: 60   解决: 26
[ 提交][ 状态][ 讨论版]

题目描述

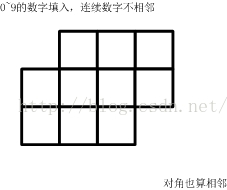
如上面的10个格子，填入0~9的数字，不能重复（原先已经填了一部分数字），要求：连续的两个数字不能相邻（左右，上下，对角都算相邻）。例如：数字0和1不能放在一起。
问：一共有多少种可能的填数方案？

输入

输入多组测试数据。
每组测试数据有三行，第一行三个整数，第二行四个整数，第三行三个整数，之间用空格隔开，分别代表每个空格所填的数，如果原先没有数，则填-1。
输入数据保证不重复数字，不保证连续数字不相邻。

输出

每组测试数据输出一行。
输出表示方案数目的整数。

样例输入

-1 -1 -1
-1 -1 -1 -1
-1 -1 -1

0 1 -1
-1 -1 -1 -1
-1 -1 -1

1 3 5
-1 -1 -1 -1
-1 -1 -1

样例输出

158008 

//思路：从第2个空至第11个空遍历填入数据，判断 每次填入的数 和 输入的数 的左、左上、上、右上满足不连续，能填到第11个数计数+1

#include <stdio.h>
#include <string.h>
#include <stdlib.h>
int a[5][5] = {-5};
int mark[11];
int count;
bool write() //写入 
{
	memset(mark,0,sizeof(mark));
	for(int i = 1;i < 11;i ++ )
	{
		if(scanf("%d",&a[i / 4][i % 4]) == EOF)
			return false;
		if(a[i / 4][i % 4] != -1)
			mark[a[i / 4][i % 4]] = 1;
	}
	return true;
}
bool judge(int x,int y,int m)
{
	if(x > 0 && abs(a[x - 1][y] - m) == 1 ) //判断上方的数是否连续 
			return false;
	if(y > 0 && abs(a[x][y - 1] - m) == 1)  //左 
		return false;
	if(x > 0 && y > 0 && abs(a[x - 1][y - 1] - m) == 1) //左上 
		return false;
	if(x > 0 && y < 3 && abs(a[x - 1][y + 1] - m) == 1) //又上 
		return false;
	return true; //四个方向都不连续 
}
void dfs(int n)  
{  
    int r, c;  
    r = n / 4; //行 
    c = n % 4; //列 
    if(n == 11) //填完十个数的出口
	{
		count ++ ;
		return ;
	}
	if(a[r][c] == -1)
	{  
        for(int i = 0;i < 10;i ++ )  //填入0~9的数 
        {
            if(!mark[i] && judge(r,c,i)) //判断填入的数是否满足条件 
            {  
                a[r][c] = i; //填入 
                mark[i] = 1; //标记 
                dfs(n + 1);
                a[r][c] = -1;  
				mark[i] = 0;
            }
        }  
    } 
    else if(judge(r,c,a[r][c]))//对输入的数据判断是否连续，若不连续返回上一层函数， 
    	dfs(n + 1);  //进入下一层，对下一个数判定 
}  
int main()
{
	while(write())
	{
		count = 0;	
		dfs(1);  //从第2个空开始填数 
		printf("%d\n",count);
	}
	return 0;
}