树属于「非线性表」的一种,有别于线性表的一对一关系,树被用来定义数据元素间的一对多关系。
现实里的树是树根朝下,枝叶朝上。而数据结构里的树,看起来像一棵倒挂的树,它是树根朝上,枝叶朝下的。
现实生活里的很多事物都可以用树结构来表示,例如:人物关系、公司组织架构、文件系统等等。
例如一个人,它只能有一个父亲,但是它可以有很多兄弟姐妹,也可能有很多孩子,这种结构就无法用简单的「线性表」去表示,但是用树就可以轻松实现。
1. 树的定义
树是n(n>=0)个结点的有限集,n=0时称为「空树」,在任意一棵非空树中:
- 有且仅有一个根(Root)结点。
- 当n>1时,其余结点可分为m(m>0)个互不相交的有限集,其中每个集合本身又是一棵树,称为根的子树。
- n>0时,根结点是唯一的,不可能存在多个根结点。
- m>0时,子树的个数没有限制,但它们一定是互不相交的。
如下,是一棵树。

如下,就不是一棵树,因为D结点和E结点相交了。

1.1 结点分类
树最顶端的节点叫作「根结点」,n>0时,树有且仅有一个根结点。
结点拥有的子树数量称为结点的「度(Degree)」,度为0的结点叫做「叶子结点」,也叫「终端结点」。度不为0的结点叫做「分支结点」,也叫「非终端结点」。
树的度是树内各结点的度的最大值。

1.2 结点关系
结点的子树的根称为该结点的「孩子」(Child),该节点被称为其孩子结点的「双亲」(Parent),同一个双亲的孩子节点互称为「兄弟」(Sibling)。
结点的「祖先」是从根结点到该结点所经分支的所有结点,以某结点为根的子树中的任一结点都称为该结点的「子孙」。
如下图中,A、B是D的祖先,C、G、H是A的子孙。

1.3 树的其它概念
结点的「层次」(Level)从根结点开始,根结点为第一层,根的孩子为第二层,以此类推。
树中结点的最大层次称为树的「深度」(Depth),也叫「高度」。

有序树和无序树
如果树中结点的各子树从左到右是有次序的,不能互换的,则称该树是有序树,否则为无序树。
森林
「森林」(Forest)是m(m>=0)棵互不相交的树的集合。对树中每个结点而言,其子树的集合就是森林。
2. 树的实现
对于「线性表」来说,将数据元素存放在一块连续的存储单元里是合理的,因为它们之间只有前后关系,存放的顺序就可以明确的反映元素间的关系。但是对于树结构来说,就不太合理了,数据元素挨个存储,谁是谁的双亲?谁又是谁的孩子呢?
单纯的数组或链表都不太好表示树结构,但是结合它俩的特点,就可以实现了。这里主要介绍树的三种表示方法:
- 双亲表示法。
- 孩子表示法。
- 孩子兄弟表示法。
2.1 双亲表示法
人可以没有孩子,但一定会有父母。在树中,除根结点外,其余节点必然有且仅有一个双亲结点。
【分析】
使用数组来顺序存储各个结点,那如何来查找结点的双亲呢?在结点中增加一个parent指针来指向其双亲结点,根结点没有双亲parent为-1。那如何查找结点的孩子呢?只能遍历整个数组,时间复杂度O(n)。
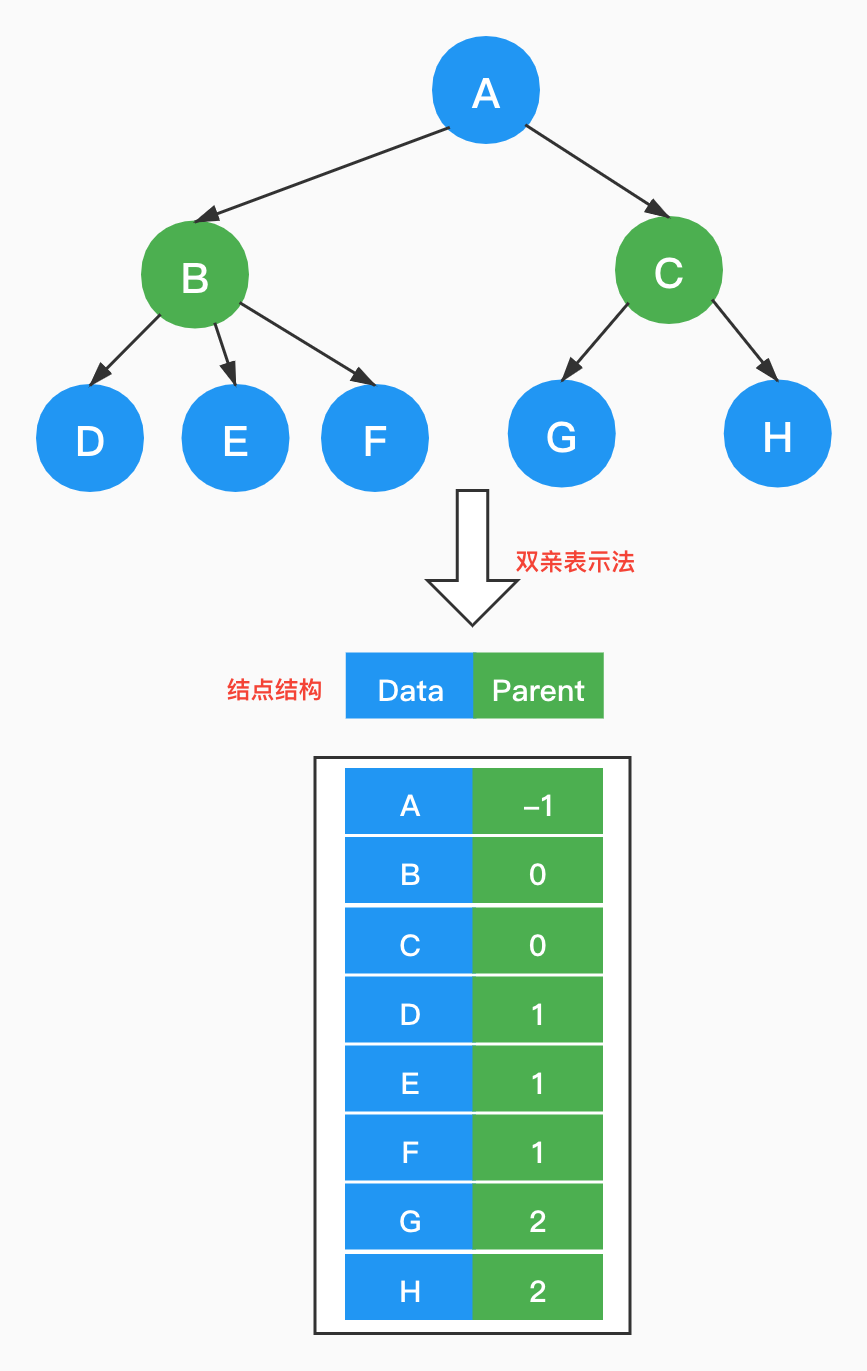
【实现】
// 双亲表示法
public class ParentTree<T> {
private int size;
private Node<T>[] table;
public ParentTree() {
this.table = new Node[16];
}
public Node<T> createRoot(T t) {
Node<T> node = new Node<>(t, -1);
table[size++] = node;
return node;
}
public Node<T> createChild(Node<T> node, T data) {
if (size == table.length) {
// 扩容
Node<T>[] newTable = new Node[table.length << 1];
for (int i = 0; i < table.length; i++) {
newTable[i] = table[i];
}
table = newTable;
}
int parent = indexOf(node);
Node<T> newNode = new Node<>(data, parent);
table[size++] = newNode;
return newNode;
}
// 父节点
public Node<T> parent(Node<T> node) {
return table[node.parent];
}
// 返回节点的所有孩子节点
public List<Node<T>> children(Node<T> node) {
List<Node<T>> children = new ArrayList<>();
int parent = indexOf(node);
for (int i = 0; i < size; i++) {
if (table[i].parent == parent) {
children.add(table[i]);
}
}
return children;
}
// 返回node的左侧兄弟节点
public Node<T> left(Node<T> node) {
Node<T> left = null;
for (int i = 0; i < size; i++) {
Node<T> n = table[i];
if (n.parent == node.parent) {
if (n == node) {
break;
}else {
left = table[i];
}
}
}
return left;
}
// 返回node的右侧兄弟节点
public Node<T> right(Node<T> node) {
Node<T> right = null;
for (int i = size - 1; i >= 0; i--) {
Node<T> n = table[i];
if (n.parent == node.parent) {
if (n == node) {
break;
} else {
right = table[i];
}
}
}
return right;
}
private int indexOf(Node<T> node) {
for (int i = 0; i < size; i++) {
if (table[i] == node) {
return i;
}
}
return -1;
}
public void show() {
for (int i = 0; i < size; i++) {
System.out.println(table[i]);
}
}
public class Node<T> {
private T data;
private int parent;
public Node(T data, int parent) {
this.data = data;
this.parent = parent;
}
public T value() {
return data;
}
@Override
public String toString() {
return String.format("[%s,%d]", data, parent);
}
}
public static void main(String[] args) {
ParentTree<String> tree = new ParentTree<>();
ParentTree<String>.Node<String> root = tree.createRoot("A");
ParentTree<String>.Node<String> b = tree.createChild(root, "B");
ParentTree<String>.Node<String> c = tree.createChild(root, "C");
tree.createChild(b, "D");
ParentTree<String>.Node<String> e = tree.createChild(b, "E");
tree.createChild(b, "F");
tree.createChild(c, "G");
tree.createChild(c, "H");
tree.show();
}
}
运行main()构建树,控制台输出:
[A,-1]
[B,0]
[C,0]
[D,1]
[E,1]
[F,1]
[G,2]
[H,2]
2.2 孩子表示法
双亲表示法中,结点使用Parent指针指向它的双亲。查找双亲的时间复杂度是O(1),但是查找孩子的时间复杂度是O(n)。
那能否换个角度,结点记录下自己有哪些孩子呢?这就需要用到孩子表示法。
双亲有且仅有一个,因此新增一个指针即可。但是结点的孩子可能有0个或多个,指针的数量是不确定的,这可如何是好?
【方案一】
孩子指针的个数为树的度,这样就可以满足最多孩子的结点要求,其它结点肯定也就满足了。缺点是对于结点的度相差很大的话,会造成大量的指针域空间浪费。

【方案二】
通过方案一的图示发现,结点会存在大量的指针域浪费的问题。因此换一种方案,指针域做变长处理,增加一个degree属性来存储结点的度。

通过图示发现,方案二解决了空间浪费的问题,结点的空间利用率提高了。但是带来了新的问题,一是结点的结构变得不一样了,二是需要维护结点的度。
【方案三】
结点按顺序存储放在数组中是合理的,但是结点的孩子数量是不确定的,因此可以创建一个链表来记录结点的孩子。树中有N个结点就有N个链表,对于叶子结点,其链表是空的。

如果要查找结点的孩子,直接遍历链表即可。那如果要查找结点的双亲呢?又得遍历整棵树了,那如何提升查找双亲的效率呢?结合「双亲表示法」,在结点中增加Parent指针即可。
【实现】
// 孩子表示法
public class ChildTree<T> {
private int size;
private Node<T>[] table;
public ChildTree() {
this.table = new Node[16];
}
public Node<T> createRoot(T t) {
Node<T> node = new Node<>(t, size, -1, 0, null);
table[size++] = node;
return node;
}
public Node<T> createChild(Node<T> node, T data) {
if (size == table.length) {
// 扩容
Node<T>[] newTable = new Node[table.length << 1];
for (int i = 0; i < table.length; i++) {
newTable[i] = table[i];
}
table = newTable;
}
Node<T> newNode = new Node<>(data, size, node.index, 0, null);
node.add(size, newNode);
table[size++] = newNode;
return newNode;
}
// 父节点
public Node<T> parent(Node<T> node) {
return table[node.parent];
}
// 返回节点的所有孩子节点
public List<Node<T>> children(Node<T> node) {
List<Node<T>> children = new ArrayList<>();
Link link = node.firstChild;
while (link != null) {
children.add(table[link.index]);
link = link.next;
}
return children;
}
// 返回node的左侧兄弟节点
public Node<T> left(Node<T> node) {
Node<T> parentNode = parent(node);
Link link = parentNode.firstChild;
Node<T> left = null;
while (link != null) {
if (link.index == node.index) {
break;
}
left = table[link.index];
link = link.next;
}
return left;
}
// 返回node的右侧兄弟节点
public Node<T> right(Node<T> node) {
Node<T> parentNode = parent(node);
Link link = parentNode.firstChild;
Node<T> right = null;
while (link != null) {
if (link.index == node.index && link.next != null) {
right = table[link.next.index];
break;
}
link = link.next;
}
return right;
}
public void show() {
for (int i = 0; i < size; i++) {
System.out.println(table[i]);
}
}
private class Node<T> {
private T data;
private int index;// 索引下标
private int parent;// 孩子+双亲表示法,提升查找parent效率
private int degree;// 度
private Link firstChild;// 长子节点
public Node(T data, int index, int parent, int degree, Link firstChild) {
this.data = data;
this.index = index;
this.parent = parent;
this.degree = degree;
this.firstChild = firstChild;
}
// 新增孩子节点,尾插法
private void add(int index, Node<T> node) {
this.degree++;
Link newLink = new Link(index, null);
if (firstChild == null) {
firstChild = newLink;
} else {
Link link = firstChild;
while (link.next != null) {
link = link.next;
}
link.next = newLink;
}
}
@Override
public String toString() {
StringBuilder sb = new StringBuilder();
sb.append(String.format("[%s,%d]", data, parent));
Link link = firstChild;
while (link != null) {
sb.append(" -> " + link.index);
link = link.next;
}
return sb.toString();
}
}
private class Link {
private int index;
private Link next;
public Link(int index, Link next) {
this.index = index;
this.next = next;
}
}
public static void main(String[] args) {
ChildTree<String> tree = new ChildTree<>();
ChildTree<String>.Node<String> root = tree.createRoot("A");
ChildTree<String>.Node<String> b = tree.createChild(root, "B");
ChildTree<String>.Node<String> c = tree.createChild(root, "C");
tree.createChild(b, "D");
tree.createChild(b, "E");
tree.createChild(b, "F");
tree.createChild(c, "G");
tree.createChild(c, "H");
tree.show();
}
}
执行main()方法构建树,控制台输出:
[A,-1] -> 1 -> 2
[B,0] -> 3 -> 4 -> 5
[C,0] -> 6 -> 7
[D,1]
[E,1]
[F,1]
[G,2]
[H,2]
2.3 孩子兄弟表示法
双亲表示法查找双亲很方便,孩子表示法查找孩子很方便。那如果要查找结点的兄弟呢?很明显它俩都不太方便。
这一次,我们站在兄弟结点的角度,去看看如何表示一棵树。
我们把结点最左边的孩子结点也叫作「长子结点」,很明显,结点的长子节点如果存在则它是唯一的,如果长子节点存在兄弟结点,则它右边的兄弟结点也是唯一的。因此,我们可以给节点增加两个指针域,分别指向它的长子结点和长子结点的右侧兄弟结点。

通过图示发现,要查找结点的孩子,直接遍历链表即可。要查找结点右侧兄弟直接通过指针即可,如果需要查找左侧兄弟结点,使用双向链表即可。如果需要查找结点的双亲,还是得遍历整棵树,或者结合双亲表示法,增加Parent指针。
【实现】
// 孩子兄弟表示法
public class SiblingTree<T> {
private int size;
private Node<T> root;
public Node<T> createRoot(T t) {
root = new Node<>(t, null, null);
return root;
}
public Node<T> createChild(Node<T> node, T data) {
Node<T> newNode = new Node<>(data, null, null);
if (node.firstChild == null) {
node.firstChild = newNode;
}else {
Node<T> child = node.firstChild;
while (child.rightSibling != null) {
child = child.rightSibling;
}
child.rightSibling = newNode;
}
return newNode;
}
// 父节点
public Node<T> parent(Node<T> node) {
// 无法直接找到,如有需要,可以在Node中增加parent指针
return null;
}
// 返回节点的所有孩子节点
public List<Node<T>> children(Node<T> node) {
List<Node<T>> children = new ArrayList<>();
Node<T> child = node.firstChild;
while (child != null) {
children.add(child);
child = child.rightSibling;
}
return children;
}
// 返回node的左侧兄弟节点
public Node<T> left(Node<T> node) {
// 无法查找,可通过parent查找,也可Node中增加leftSibling指针
return null;
}
// 返回node的右侧兄弟节点
public Node<T> right(Node<T> node) {
return node.rightSibling;
}
public void show(Node<T> node) {
System.out.println(node);
Node<T> child = node.firstChild;
while (child != null) {
show(child);
child = child.rightSibling;
}
}
private class Node<T> {
private T data;
private Node<T> firstChild;
private Node<T> rightSibling;
public Node(T data, Node<T> firstChild, Node<T> rightSibling) {
this.data = data;
this.firstChild = firstChild;
this.rightSibling = rightSibling;
}
@Override
public String toString() {
return String.format("[%s,%s,%s]", data, firstChild != null ? firstChild.data : null,
rightSibling != null ? rightSibling.data : null);
}
}
public static void main(String[] args) {
SiblingTree<String> tree = new SiblingTree<>();
SiblingTree<String>.Node<String> root = tree.createRoot("A");
SiblingTree<String>.Node<String> b = tree.createChild(root, "B");
SiblingTree<String>.Node<String> c = tree.createChild(root, "C");
tree.createChild(b, "D");
tree.createChild(b, "E");
tree.createChild(b, "F");
tree.createChild(c, "G");
tree.createChild(c, "H");
tree.show(tree.root);
}
}
运行main()构建树,控制台输出:
[A,B,null]
[B,D,C]
[D,null,E]
[E,null,F]
[F,null,null]
[C,G,null]
[G,null,H]
[H,null,null]
3. 二叉树
二叉树是比较常用,需要重点了解的一种特殊的树。例如对于「折半查找」算法,使用二叉树就可以很轻松的实现。
3.1 二叉树的定义
二叉树(Binary Tree)是n(n>=0)个结点的有限集合,它由一个根结点和两颗互不相交的左右二叉子树组成。
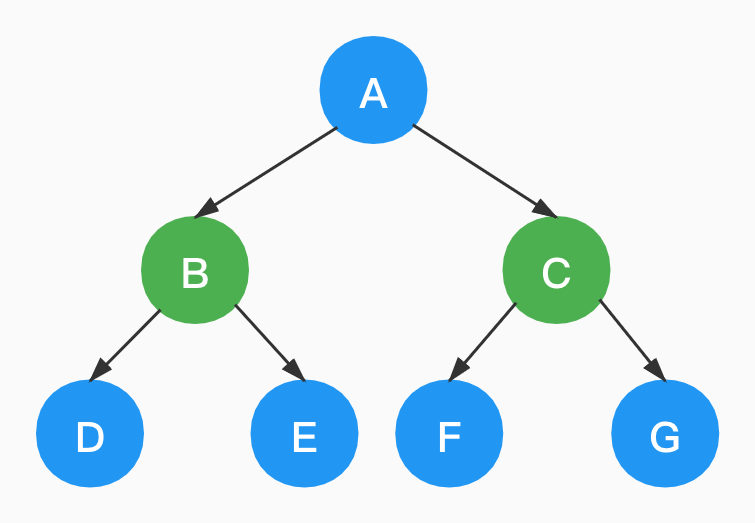
前面图示中的树就不是一棵二叉树,因为结点B有D、E、F三个孩子节点,不符合二叉树的定义。
如下,是一棵二叉树。

3.2 二叉树的特点
- 每个结点最多有两棵子树,二叉树中不存在度大于2的结点。
- 二叉树是有序树,左右子树是有顺序的,不可互换。
- 即使结点只有一棵子树,也要区分是左子树还是右子树。
3.3 特殊的二叉树
3.3.1 斜树
斜树分为:左斜树和右斜树。
所有的结点都只有左子树的叫作「左斜树」,所有的结点都只有右子树的叫作「右斜树」。
斜树是一棵特殊的二叉树,它看起来或许都不像是树,反而更像链表了。

3.3.2 满二叉树
符合以下定义的则为「满二叉树」:
- 所有分支结点都存在左右子树。
- 所有叶子结点否都在同一层上。
如下,就是一棵满二叉树。如果删除任一结点,都不再是满二叉树。
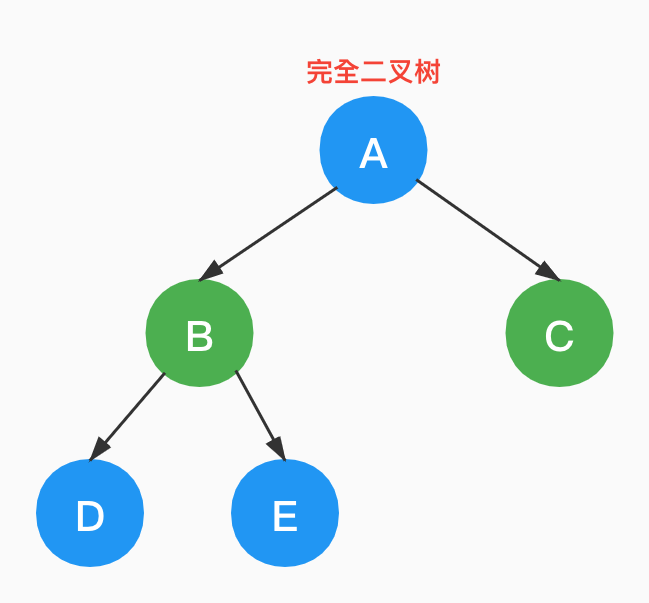
3.3.3 完全二叉树
对一棵具有n个结点的二叉树按层序编号,如果编号为i(1<=i<=n)的结点与同样深度的满二叉树中编号为i的结点在二叉树中的位置完全相同,则这棵树为完全二叉树。
完全二叉树不一定是满二叉树,但是满二叉树一定是完全二叉树。
完全二叉树的特点:
- 叶子结点只能出现在最下两层。
- 最下层的叶子结点一定集中在左边连续位置。
- 倒数第二层如果存在叶子节点,则一定集中在右边连续位置。
- 如果结点度为1,则它只有左子树。
- 同样结点个数的二叉树,完全二叉树高度最小。
如下是一棵完全二叉树。
如下是一棵非完全二叉树。

3.4 二叉树的性质
1. 二叉树在第i层最多有2i-1个结点。
以满二叉树为例,第1层有1个结点,第2层有2个节点,第三层有4个结点…,通过数学归纳计算可得,第i层最多有2i-1个结点。

2. 深度为k的二叉树最多有2k-1个结点。
以满二叉树为例,高度为1的树有1个结点,高度为2的树有3个结点,高度为3的树有7个结点,通过数学归纳计算可得,高度为k最多有2k-1个结点。
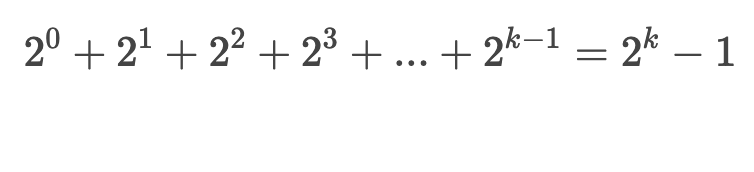
3. 对于任何一棵二叉树T,如果叶子结点数为n,度为2的结点数为m,则n=m+1。
4. 具有n个结点的完全二叉树,深度为「log2n」+1。
5. 对一棵有n个结点的完全二叉树的结点按层序编号,对任一结点i(1<=iN=n)有:
- 如果i=1,则结点i是二叉树的根。如果n>1,则其双亲节点是「i/2」。
- 如果2i>n,则i无左子树;否则其左子结点是2i。
- 如果2i+1>n,则结点i无右子树;否则其右子结点是2i+1。
3.5 二叉树的存储
3.5.1 顺序存储
对于多叉树,顺序存储比较困难。但是对于完全二叉树,由于其结点定义严格,因此使用顺序存储也可以很好表示。

那对于非完全二叉树呢?是否可以顺序存储?其实将它转换成完全二叉树即可,不存在的结点存储null,会浪费一定的存储空间。

3.5.2 链式存储
非完全二叉树虽然也能顺序存储,但是会造成空间的浪费,应当有限考虑链式存储。
因为二叉树的每个结点度最大为2,因此我们可以这样来定义结点结构。

Data存储数据,Left指针指向左子结点,Right指针指向右子结点。
因此,二叉树可以这样存储。

双亲找孩子非常简单,但是孩子找双亲就不那么容易了,需要遍历整棵树,也可以在结点中加一个Parent指针来解决查找双亲的问题。
3.6 二叉树的遍历
二叉树的遍历方式有:
- 前序遍历。
- 中序遍历。
- 后序遍历。
- 层序遍历。
二叉树的便利很重要,篇幅原因,这里不展开,会专门写一篇文章实现这些遍历算法。
4. 总结
有别于线性表的一对一关系,树可以用来定义元素间的一对多关系。本篇文章介绍了树的概念和特性,以及如何来存储树的三种表现形式。双亲表示法查找双亲很方便,孩子表示法查找孩子结点很方便,孩子兄弟表示法查找孩子和兄弟结点很方便,实际应用中,我们不应该拘泥于一种方法,而是相互结合,最高效率的实现算法需求。
说完树后,我们又介绍了经常使用的二叉树,它是一种特殊的树,可以很方便的实现「折半查找」。还介绍了二叉树的一些特性,很多特性都是通过数学公式推导出来的,因此学习数据结构大家有必要再复习一下数学知识。
关于二叉树的四种遍历方式,篇幅原因,这里没有展开,笔者会在后面的文章详细说明。

























 4909
4909

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










