C++ 吃透回溯算法

感谢博主代码随想录的视频分享
下文总结皆根据上述视频总结记录

1. 回溯算法的核心

1.1. 介绍

回溯算法都可以抽象成一个N叉树, 每个节点都是处理集合的大小, 树的深度是递归

    回溯法是优先搜索的一种特殊情况, 常用需要记录节点状态的深度优先搜索策略, 通常比如排列, 组合, 选择类问题使用回溯法;
    在搜搜某一个节点时候, 如果发现目前节点并不是目标节点, 我们回退到原来节点继续搜索, 并且把目前节点修改的状态还原.
    具体写法:

• 修改当前节点状态–>递归子节点–>回改当前节点
• 诀窍: 按引用传状态; 所有状态修改在递归完成后回改

解决什么问题?
组合, 切割, 子集, 排序, 棋盘

1.2. 回溯算法结构

void backTracking(	ans,  // 保存结果的数组 
					nums, // 输入
					visited, // 树枝去重使用, 可选
					temp, // 保存中间数据的数组
					target, // 终止条件
					start){ // 叶子节点的起始位置
    if(终止条件满足结果){ 收集结果; return}; 
    for(遍历nums 从start开始的所有子节点){ // 单层搜索
        交换; // temp.push_back(nums[i]); visited[i-1] = true;
        递归; // backTracking(ans, nusm, visited, temp, target, i或i+1)
        换回; // temp.pop_back(nums[i]); visited[i-1] = false;
    }
}

2. 具体应用

在下面的所有应用中, 你会发现所有代码都会严格参考上面给出的回溯代码格式完成, 因此当要类型问题时, 先考虑框架, 在进行细节完善, 做到事半功倍;

关键点需要注意:

• 去重需要对输入数组进行排序, 这个去重去的是输入数组[1,1,2]里面的 [1,2], [1,2] 这种重复
• 是否重复当前值是在TrackBack的start位置输入i+1表示不重复, 输入i表示重复, 这个去重去的是输入数组[1,2,3] 里面的 1,1,1, 1,1,2, 1,1,3
• 剪枝都是在for上剪枝的

2.1. 组合

77-组合

给定两个整数 n 和 k，返回 1 … n 中所有可能的 k 个数的组合。

输入: n = 4, k = 2
输出: [[2,4],  [3,4],  [2,3],  [1,2],  [1,3],  [1,4],]

• 这里可以将每次的for想象成遍历当前节点的所有子节点

class Solution {
public:

// 组合: 输入 4, 2, 12 13 14 23 24 34
void TrackBacing_combination(vector<vector<int>> &ans, // 结果
    int n, int k, // 问题输入
    int start,  // 层序遍历的起点
    vector<int> &temp ){ // 临时数组

    if(temp.size() == k){
        ans.push_back(temp);
        return;
    }
    for(int i=start; i<=n; i++){ // 从start到n, 就能够保证元素不重复, 因为start以前的都包含了
        temp.push_back(i);
        TrackBacing_combination(ans, n, k, i+1, temp); // 告诉下一层递归从start+1开始
        temp.pop_back();
    }
}

    vector<vector<int>> combine(int n, int k) {
        vector<vector<int>> ans; 
        vector<int> temp;
        TrackBacing_combination(ans, n, k, 1, temp);
        return ans;
    }
};

• 剪枝: 确定当前与目标的距离, 在for循环中剪枝

    // 从start到n, 就能够保证元素不重复i+1, 因为start以前的都包含了
    // 然后剪枝操作, k-temp.size()是`还缺多少个`, n-是`还有多少个`
    for(int i=start; i<=n-(k-temp.size())+1; i++){ 
        temp.push_back(i);
        TrackBacing_combination(ans, n, k, i+1, level+1, temp); // 告诉下一层递归从start+1开始
        temp.pop_back();
    }

39.组合总和

给定一个无重复元素的正整数数组 candidates 和一个正整数 target ，找出 candidates 中所有可以使数字和为目标数 target 的唯一组合

输入: candidates = [2,3,6,7], target = 7
输出: [[7],[2,2,3]]

输入: candidates = [2,3,5], target = 8
输出: [[2,2,2,2],[2,3,3],[3,5]]

输入: candidates = [2], target = 1
输出: []

输入: candidates = [1], target = 1
输出: [[1]]

输入: candidates = [1], target = 2
输出: [[1,1]]

特点:

• 给定元素无重复

• 结果可重复 回溯时输入的为i保证可重复
  
  

• 剪枝: 主要是将candidates进行排序, 这样当遍历子节点时, 就能判断后面的子节点超出所求范围了 && sum+nums[i] <= target;

class Solution {
public:
    void TrackBacking_cut(vector<vector<int>>& ans, 
                    vector<int>& nums,
                    int target,
                    int sum,
                    int start, 
                    vector<int> &temp){ // 中间temp
        // 收割结果, 也就是递归终止条件
        if(sum > target) return;
        if(sum == target){
            ans.push_back(temp);
        }

        // 增加&& sum+nums[i] <= target; 进行剪枝
        for(int i=start; i<nums.size() && sum+nums[i] <= target; i++){
            temp.push_back(nums[i]);
            sum += nums[i];
            // 因为元素可以重复使用, 所以这里传入的是i, 如果不重复, 就是i+1
            TrackBacking_cut(ans, nums, target, sum, i, temp); 
            sum -= nums[i];
            temp.pop_back();
        }
    }

    vector<vector<int>> combinationSum(vector<int>& candidates, int target) {
        sort(candidates.begin(), candidates.end());
        vector<vector<int>> ans;
        vector<int> temp;
        TrackBacking_cut(ans, candidates, target, 0, 0, temp);
        return ans;
    }
};

40.组合总和II

特点

• 候选值只能有一次出现
• 候选值有重复

输入: candidates = [10,1,2,7,6,1,5], target = 8,
输出: [ [1,1,6],  [1,2,5], [1,7], [2,6]]

输入: candidates = [2,5,2,1,2], target = 5,
输出: [[1,2,2],[5]]

思考:

• 由于给出的candidates里面可能会有重复, 所以当进行一个节点10的子节点1,2,7,6,1,5遍历时, 会出现相同节点 1, 1的遍历, 所以这里需要思考如何去掉一个遍历的1呢
• 解决方案是: 通过增加一个监视器nums[i] == nums[i-1] && visited[i-1] = true 表示上一个节点与当前节点重复, 并且上一个节点被用过了, 所以这里就可以将当前节点的子节点遍历忽略掉;
• 为何是nums[i] == nums[i-1]就能判断呢?
• 因为我们需要先将candidates进行排序
  

class Solution {
public:
    void backTracking(vector<vector<int>> &ans, 
                        vector<int>&nums, int target, 
                        vector<int>& temp, 
                        vector<bool>& visited, 
                        int sum=0, int start=0){
        
        if(sum > target) return;
        if(sum == target) {
            ans.push_back(temp);
            return;
        }

        // visited[i-1]标识同一个值, 在同一层, 使用过, 所以当前这个值就可以被略过了, 因为下面的for里面遍历的值就是同一个节点的不同的子节点
        for(int i=start; i<nums.size() && sum+nums[i] <= target; i++){
            if(i>0 && nums[i] == nums[i-1] && !visited[i-1]) continue;
            // if(i>0 && nums[i] == nums[i-1] ) continue; // 不能这样做, 这是因为直接前后相等, 会把1,1,6这种情况给去掉

            visited[i] = true;
            sum += nums[i];
            temp.push_back(nums[i]);
            backTracking(ans, nums, target, temp, visited, sum, i+1);
            temp.pop_back();
            sum -= nums[i];
            visited[i] = false;
        }
    }

    vector<vector<int>> combinationSum2(vector<int>& candidates, int target) {
        sort(candidates.begin(), candidates.end()); // 排序后面才能使用visited进行识别
        vector<vector<int>> ans;
        vector<int> temp;
        vector<bool> visited(candidates.size(), false);
        backTracking(ans, candidates, target, temp, visited); // 添加visited用来标识对于重复值时, 不在遍历
        return ans;
    }
};

2.2. 切割

131. 分割回文串

给你一个字符串 s，请你将 s 分割成一些子串，使每个子串都是 回文串 。返回 s 所有可能的分割方案。
回文串 是正着读和反着读都一样的字符串。

输入：s = "aab"
输出：[["a","a","b"],["aa","b"]]
输入：s = "a"
输出：[["a"]]

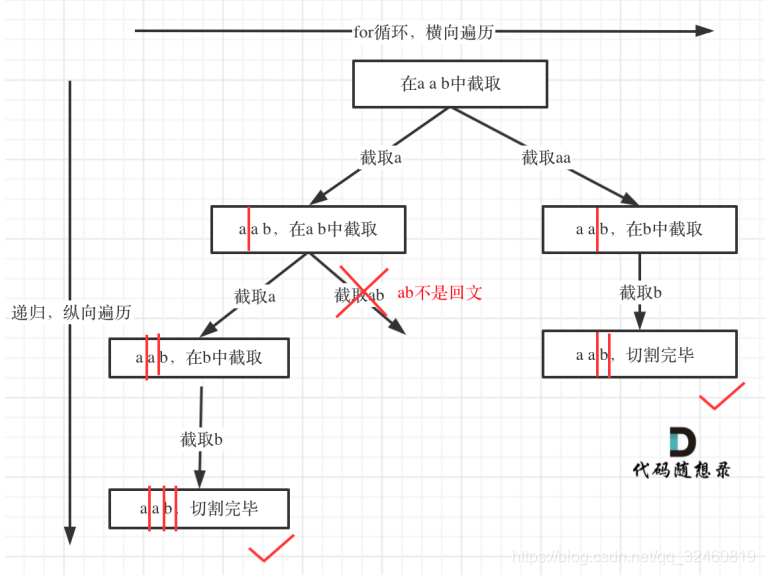
思路:

• 切割一个a后, 在bcdef中在去切割, 切割b后在cdef中切割第三段…
  

class Solution {
public:
    bool isPatition(const string &s, int start, int end){
        for(int i=start, j=end; i<j; i++, j--){
            if(s[i] != s[j]){
                return false;
            }
        }
        return true;
    }

    void trackBacking(const string &s, 
                    vector<vector<string>> &ans, 
                    vector<string> &temp, // 放回文
                    int start){
        if(start >= s.size()) {
            ans.push_back(temp);
            return;
        }


        for(int i=start; i<s.size(); i++){
            // s[start,i]是否是回文子串
            if(isPatition(s, start, i)){
                // 判断是回文子串就加入到临时变量中, 然后判断下一个
                string str = s.substr(start, i-start+1);
                temp.push_back(str);
                trackBacking(s, ans, temp, i+1);
                temp.pop_back();
            }else{
                continue;
            }

        }
    }

    vector<vector<string>> partition(string s) {
        vector<vector<string>> ans;
        vector<string> temp;
        trackBacking(s, ans, temp, 0);
        return ans;
    }
};

总结:

• 切割问题其实可以想象成组合问题
• 如何模拟切割线
• 切割问题的终止条件
• 如何判断回文

93. 复原 IP 地址

这个题跟上面的回文子串的问题相似
给定一个只包含数字的字符串，用以表示一个 IP 地址，返回所有可能从 s 获得的 有效 IP 地址 。你可以按任何顺序返回答案。
有效 IP 地址 正好由四个整数（每个整数位于 0 到 255 之间组成，且不能含有前导 0），整数之间用 ‘.’ 分隔。
例如：“0.1.2.201” 和 “192.168.1.1” 是 有效 IP 地址，但是 “0.011.255.245”、“192.168.1.312” 和 “192.168@1.1” 是 无效 IP 地址。

输入：s = "25525511135"
输出：["255.255.11.135","255.255.111.35"]
输入：s = "0000"
输出：["0.0.0.0"]
输入：s = "1111"
输出：["1.1.1.1"]
输入：s = "010010"
输出：["0.10.0.10","0.100.1.0"]
输入：s = "101023"
输出：["1.0.10.23","1.0.102.3","10.1.0.23","10.10.2.3","101.0.2.3"]

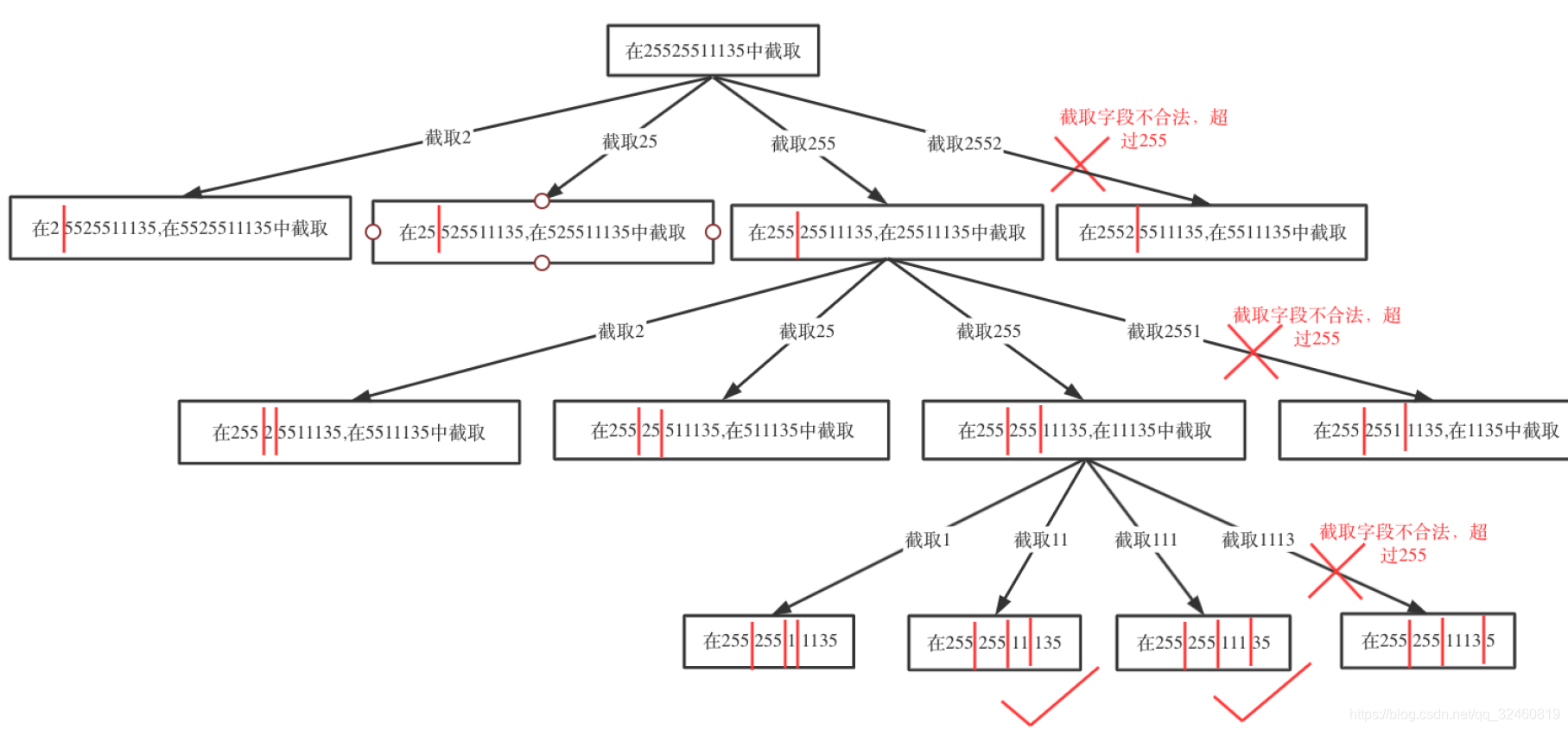
• start: 记录下一层递归分割的起始位置
• pointNum: 添加逗号的数量
• 递归终止条件: 由于要求是4段, 因此不能用切割线到最后作为终止条件, 而是分割段数
• pointNum==3 并且 第四段是否合法

剪枝操作示意图

class Solution {
private:
    vector<string> result;// 记录结果
    // start: 搜索的起始位置，pointNum:添加逗点的数量    
    void backtracking(string& s, int start, int pointNum) {
        if (pointNum == 3) { // 逗点数量为3时，分隔结束
            // 判断第四段⼦字符串是否合法，如果合法就放进result中
            if (isValid(s, start, s.size() - 1)) {
                result.push_back(s);
            }
            return;
        }
        for (int i = start; i < s.size(); i++) {
            if (isValid(s, start, i)) { // 判断 [start,i] 这个区间的⼦串是否合法
                s.insert(s.begin() + i + 1 , '.');  // 在i的后⾯插⼊⼀个逗点
                pointNum++;
                backtracking(s, i + 2, pointNum);   // 插⼊逗点之后下⼀个⼦串的起始位置为i+2
                pointNum--;                         // 回溯
                s.erase(s.begin() + i + 1);         // 回溯删掉逗点
            } else break; // 不合法，直接结束本层循环
        }
    }
    // 判断字符串s在左闭⼜闭区间[start, end]所组成的数字是否合法
    bool isValid(const string& s, int start, int end) {
        if (start > end) {
            return false;
        }
        if (s[start] == '0' && start != end) { // 0开头的数字不合法
                return false;
        }
        int num = 0;
        for (int i = start; i <= end; i++) {
            if (s[i] > '9' || s[i] < '0') { // 遇到⾮数字字符不合法
                return false;
            }
            num = num * 10 + (s[i] - '0');
            if (num > 255) { // 如果⼤于255了不合法
                return false;
            }
        }
        return true;
    }
public:
    vector<string> restoreIpAddresses(string s) {
        result.clear();
        if (s.size() > 12) return result; // 算是剪枝了
        backtracking(s, 0, 0);
        return result;
    }
};

2.3. 子集

2.4. 排序

排序问题与组合问题还是有些区别和差异的

1. 排序是有序的, 也就是说[1,2]和[2,1]是两个集合, 所以排列问题不能使用start进行层遍历, 而是每次都用0-n进行回溯遍历
2. 排列问题也会用到visited进行标记, visited[i] = true, 表示当前搜搜路径已经包含了当前值, 所以需要给continue掉当前节点, 话不多说, 请看下例

46 全排序

给定一个不含重复数字的数组nums ，返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。

输入：nums = [1,2,3]
输出：[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]
输入：nums = [0,1]
输出：[[0,1],[1,0]]
输入：nums = [1]
输出：[[1]]

• 终止条件: 路径长度等于input长度
• 跳出条件: visited[i] = true; continue

class Solution {
public:

    void trackBacking(vector<int> &nums, // 输入数组
                    vector<vector<int>> &ans, // 结果保存
                    vector<int> & temp, // 临时路径
                    int start,  // 层序遍历起点
                    vector<bool> & visited){ // 该节点已经被插入进去了
        if(temp.size() == nums.size()) {
            ans.push_back(temp);
            return;
        }

        for(int i=start; i<nums.size(); i++){
            if(visited[i] == true) continue;

            visited[i] = true;
            temp.push_back(nums[i]);
            trackBacking(nums, ans, temp, 0, visited);
            temp.pop_back();
            visited[i] = false;
        }

    }
    vector<vector<int>> permute(vector<int>& nums) {
        if(nums.empty()) return {};

        vector<vector<int>> ans;
        vector<int> temp;
        vector<bool> visited(nums.size(), false);
        trackBacking(nums, ans, temp, 0, visited);
        return ans;
    }
};

类似的题目:

input = "ABC";
output = [ABC, ACB, BCA, BAC, CAB, CBA]

47.全排列II

输入：nums = [1,1,2]
输出：[[1,1,2], [1,2,1], [2,1,1]]

输入：nums = [1,2,3]
输出：[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]

• 与上一个题的区别: 给出的元素中有重复的, 所以需要去重
• 去重的逻辑操作跟组合里面的去重一致, 先进行排序, 然后在利用visited[i-1]==false去重
• 为何是visited[i-1]==false这里在强调一下, 因为visited[i-1]遍历完, 会置成false才能表示上一个节点完成了
  

class Solution {
public:
    void trackBacking(vector<int> &nums, vector<vector<int>>& ans, vector<int>&temp, int start, vector<bool> &visited){
        if(temp.size() == nums.size()) {
            ans.push_back(temp);
            return;
        }

        for(int i=start; i<nums.size(); i++){
            if(visited[i] == true) continue;
            if(i>0 && nums[i] == nums[i-1] && visited[i-1] == false) continue;

            visited[i] = true;
            temp.push_back(nums[i]);
            trackBacking(nums, ans, temp, 0, visited);
            temp.pop_back();
            visited[i] = false;
        }
    }

    vector<vector<int>> permuteUnique(vector<int> &nums) {
        vector<vector<int>> ans;
        vector<int> temp;
        vector<bool> visited(nums.size(), false);
        sort(nums.begin(), nums.end());
        trackBacking(nums, ans, temp, 0, visited);
        return ans; 
    }
};

2.5. 棋盘

2.6. 路径搜索

二维数组需要删除多少个障碍物才能从起点到达终点

给定一个 n行字符串, 每个字符串由.和#组成, #表示障碍, 求从0,0点 到n,m点最少删除多少个障碍物能够到达

思考:

• 二维数组深度搜索
• 遇到障碍物就删掉障碍物, 然后继续深度搜索
• 设定监视器 visited标记当前点在深度遍历中遍历过

#include <vector>
#include <iostream>
#include <algorithm>
#include <unordered_map>
#include <stdio.h>
#include <unistd.h> 
using namespace std;

vector<int> direction = {-1, 0, 1, 0, -1}; // 上下左右的向导
void backTracking(vector<string> &nums,  // 二维数组保存整个地图
    int i, int j, // 遍历当前节点
    vector<vector<bool>>&visited, // 是否遍历过当前这个点
    vector<int> &ans, // 保存每个到达终点路径需要消除的障碍数量
    int obstacle){ // 保存当前遇到障碍物的数量
    cout<<i<<" "<<j<<endl;

    // 超出边界直接返回
    if(i<0 || i>=nums.size() || j<0 || j>=nums[0].size()) {
        cout<<"越界了"<<endl;
        return;
    }

    // 遍历过就放弃
    if(visited[i][j]) {
        cout<<"遍历过了"<<endl;
        return;
    }

    // 当前这个点是障碍物就加入进去
    if(nums[i][j] == '#') obstacle++;

    // 遍历到终点了
    if(i==nums.size()-1 && j==nums[0].size()-1){
        cout<<"到终点了========"<<obstacle<<endl;
        ans.push_back(obstacle);
        return;
    }

    // visited 回溯
    visited[i][j] = true;
    for(int k=0; k<4; k++){
        int x=i+direction[k], y=j+direction[k+1];
        backTracking(nums, x, y, visited, ans, obstacle);
    }
    visited[i][j] = false;
}

int main(int argc, char const *argv[])
{
    // vector<string> nums = { ".##", 
    //                         "##.", 
    //                         "..."};
    vector<string> nums = { ".####", 
                            "###..", 
                            "..###"};
    int n=nums.size(), m=nums[0].size();

    vector<vector<bool>> visited(n, vector<bool>(m, false));
    vector<int> ans;
    backTracking(nums, 0,0, visited, ans, 0);

    // 打印每一条路径下删除的障碍物数量
    for(const int & res : ans){
        cout<<res << " ";
    }cout<<endl;

    cout<<"因此, 想要到达终点, 删除障碍物最少"<<*min_element(ans.begin(),ans.end())<<endl;
    return 0;
}

79-单词搜索

给定一个 m x n 二维字符网格 board 和一个字符串单词 word, 如果 word 存在于网格中，返回 true ；否则，返回 false 。

输入：board = [
["A","B","C","E"],
["S","F","C","S"],
["A","D","E","E"]], 
word = "ABCCED"
输出：true

vector<int> direction = {-1, 0, 1, 0, -1};

// 要把所有的可能都放进去
void backTracking(  vector<vector<char>>& board, int i, int j,
                    string &word, bool & find,
                    vector<vector<bool>> &visited, 
                    int level){
    // 越界直接返回
    if(i<0 || i>=board.size() || j<0 || j>=board[0].size()){
        return;
    }
    // 已经找到, 或者当前位置已经遍历过, 或者不符合要求, 直接返回
    if(visited[i][j] || find || board[i][j] != word[level]){
        return;
    }
    // 已经是最后一一个, 都已经符合了, 直接返回true
    if(level == word.size()-1) {
        find = true;
        return;
    }
    // 当前节点遍历完成, 
    visited[i][j] = true; // 修改当前节点
    for(int k=0; k<4; k++){
        int x=i+direction[k], y=j+direction[k+1];
        backTracking(board, x, y, word, find, visited, level+1);
    }
    visited[i][j] = false; // 修改当前节点
}


// 字符矩阵查路径
bool exist(vector<vector<char>>& board, string word) {
    if(board.empty() || board[0].empty()) return false;
    int m=board.size(), n=board[0].size();
    vector<vector<bool>> visited(m, vector<bool>(n, false));

    bool find = false;
    for(int i=0; i<m; i++){
        for(int j=0; j<n; j++){
            backTracking(board, i, j, word, find, visited, 0);
        }
    }
    return find;
}

2.7 全排序列下的组合

题目: 从数组nums中找出所有和为target的组合

nums = {1,2,4} target=5
结果
1 1 1 1 1 
1 1 1 2 
1 1 2 1 
1 2 1 1 
1 2 2 
1 4 
2 1 1 1 
2 1 2 
2 2 1 
4 1

粉色为成功命中结果, 绿色为剪枝

void TrackBacking_cut(vector<vector<int>>& ans, 
                vector<int>& nums,
                int target,
                int sum,
                int start, 
                vector<int> &temp,
                vector<bool> &visited){ // 中间temp
    // 收割结果, 也就是递归终止条件
    if(sum > target) return;
    if(sum == target){
        ans.push_back(temp);
    }

    // 增加&& sum+nums[i] <= target; 进行剪枝
    for(int i=start; i<nums.size() && sum+nums[i] <= target; i++){
        temp.push_back(nums[i]);
        sum += nums[i];
        // 因为元素可以重复使用, 并且没有顺序使用, 所以这里每次都是从 0开始
        TrackBacking_cut(ans, nums, target, sum, 0, temp, visited); 
        sum -= nums[i];
        temp.pop_back();
    }

}

void combinationSum(int target = 5) {
    vector<int> candidates = {1,2,4};
    vector<vector<int>> ans;
    vector<int> temp;
    vector<bool> visited(candidates.size(), false);
    TrackBacking_cut(ans, candidates, target, 0, 0, temp, visited);
    print_vv(ans);
}