题意:
有一个长度为n(n<=2e5)的序列,q(q<=2e5)次操作
序列中的每个位置对应一个数ai(1<=ai<=5e5)
每次操作给一个数x,代表挑出的序列中的下标为x的数
若对应下标的数已经被挑出,那么就把它放回去
每次操作完,询问所有挑出的数中互质的对数
刚开始时所有数都没有被挑出
思路:
刚开始的没有数被挑出,那么初始答案为0。
令num[i] :挑出的数中 i 的个数
如果当前操作的数为x,那么对答案的贡献
如果是挑出则加,放入则减,注意x==1的情况
反演一下贡献的式子:
转化枚举量:
到这里可以发现,预处理每个数的有效因子,用树状数组维护每个d的前缀和
就能在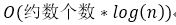
代码:
#include<bits/stdc++.h>
#define lowbit(x) (x&(-x))
const int N = 5e5+10;
using namespace std;
vector<int>pr,fro[N],E[N];
bool Np[N];
int mu[N];
void init(){
mu[1] = 1;
for(int i=2;i<N;i++){
if(!Np[i]){
mu[i] = -1;
pr.emplace_back(i);
}for(int j=0,k=pr[0]*i;k<N;k=pr[++j]*i){
Np[k] = true;
if(i%pr[j]==0){
mu[k] = 0;
break;
}mu[k] = -mu[i];
}
}for(int i=1;i<N;i++)if(mu[i]){
fro[i].emplace_back(0);
for(int j=i;j<N;j+=i){
E[j].emplace_back(i);
fro[i].emplace_back(0);
}
}
}
inline void add(int d,int x,int val){
int n = fro[d].size();
while(x<n){
fro[d][x]+=val;
x += lowbit(x);
}
}
inline long long query(int d,int x){
long long res = 0;
while(x){
res += fro[d][x];
x -= lowbit(x);
}return res;
}
long long work(int x){
long long res = 0;
for(int i=0;i<E[x].size();i++){
int d = E[x][i];
long long tmp = 0;
tmp += query(d,500000/d);
res += tmp * mu[d];
}return res;
}
void oper(int x,int val){
for(int i=0;i<E[x].size();i++){
int d = E[x][i];
add(d,x/d,val);
}
}
int A[N];
bool has[N];
int main()
{
init();
int n,q,x;
scanf("%d%d",&n,&q);
for(int i=1;i<=n;i++){
scanf("%d",&A[i]);
}long long ans = 0;
while(q--){
scanf("%d",&x);
long long num = work(A[x]);
if(!has[x]){
ans += num;
oper(A[x],1);
}else {
if(A[x]==1)num--;
ans -= num;
oper(A[x],-1);
}has[x] = !has[x];
printf("%I64d\n",ans);
}return 0;
}








 本文介绍了一种解决特定问题的算法实现:在一个长度为n的序列中进行操作,通过挑选或放回某个位置的数,并计算已挑出的数中互质对的数量。文章详细解释了算法思路,包括预处理有效因子、使用树状数组维护前缀和等步骤。
本文介绍了一种解决特定问题的算法实现:在一个长度为n的序列中进行操作,通过挑选或放回某个位置的数,并计算已挑出的数中互质对的数量。文章详细解释了算法思路,包括预处理有效因子、使用树状数组维护前缀和等步骤。

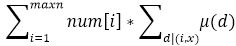
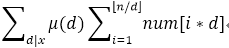
















 1314
1314

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








