题意:
给定一个大小为n(n<=1e5)的数字(ai<=1e6)集合,q次询问
每次询问给往集合中插入一个数,求当前集合的贡献
集合的贡献为所有大小为k的集合的gcd之和
思路:
f[ x ]:集合大小为k且gcd()==x的集合数量
num[ x ]:所有的数中x倍数的个数
那么答案为
刚开始想歪了:
想用树状数组维护后面的部分,均摊复杂度应该能过。。
但是维护树状数组的复杂度和约数个数有很大的关系
x的范围内,约数个数最多有240个,那么更新的复杂度达到O(8000log())
然后就TLE了
重新分析,发现也可以这么求:
就很容易了。。。
代码:
#include<bits/stdc++.h>
const int mod = 1e9+7;
const int N = 1e6+10;
using namespace std;
vector<int>pr,E[N];
int n,k,q,mu[N],num[N],fro[N],ni[N],f[N],A[N];
bool Np[N];
long long ans = 0;
inline long long qpow(long long x,long long y){
long long res = 1;
while(y){
if(y&1)res = res * x % mod;
y>>=1;
x = x * x % mod;
}return res;
}
inline long long C(int n,int m){
return 1LL * fro[n] * ni[m] % mod * ni[n-m] % mod;
}
void init(){
mu[1] = fro[0] = fro[1] = ni[0] = 1;
for(int i=2;i<N;i++){
fro[i] = 1LL * fro[i-1] * i % mod;
if(!Np[i]){
pr.emplace_back(i);
mu[i] = -1;
}for(int j=0,k=pr[0]*i;k<N;k=pr[++j]*i){
Np[k] = true;
if(i%pr[j]==0){
mu[k] = 0;
break;
}mu[k] = -mu[i];
}
}ni[N-1] = qpow(fro[N-1],mod-2);
for(int i=N-1;i>1;i--){
ni[i-1] = 1LL * ni[i] * i % mod ;
}
for(int i=1;i<N;i++){
for(int j=i;j<N;j+=i){
num[i] += A[j];
E[j].emplace_back(i);
}
}
for(int i=N-1;i>=1;i--){
A[i] = 0;
if(num[i]>=k){
A[i] = C(num[i],k);
for(int j=0;j<E[i].size();j++){
int d =E[i][j];
f[d] += mu[i/d] * A[i];
if(f[d]>=mod)f[d]-=mod;
else if(f[d]<0)f[d]+=mod;
}
}if(f[i])ans = (ans+1LL*f[i]*i)%mod;
}
}
inline int read()
{
int x=0,f=1; char ch=getchar();
while (ch<'0' || ch>'9') {if (ch=='-') f=-1; ch=getchar();}
while (ch>='0' && ch<='9') {x=x*10+ch-'0'; ch=getchar();}
return x*f;
}
inline void work(int x){
for(int i=0;i<E[x].size();i++){
int d = E[x][i];
if( (ans -= 1LL*f[d]*d%mod) < 0 ) ans+=mod;
}
for(int i=E[x].size()-1,sum=0;i>=0;i--){
int d = E[x][i];
num[d]++;
if(num[d]>=k){
int de = C(num[d],k) - A[d];
A[d] = de + A[d];
if(de<0)de+=mod;
for(int j=0;j<E[d].size();j++){
int dd = E[d][j];
f[dd] += mu[d/dd] * de ;
if(f[dd]>=mod)f[dd]-=mod;
else if(f[dd]<0)f[dd]+=mod;
}
}ans = (ans+1LL*f[d]*d)%mod;
}
}
int main()
{
n = read();k = read();q = read();
for(int i=0;i<n;i++){
A[read()]++;
}init();
while(q--){
work(read());
printf("%I64d\n",ans);
}return 0;
}












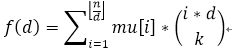














 416
416

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








