题意及官方题解:
思路:看到另一种做法,要巧妙一点,记录一下
解法一(官方):
打出当前位对后面位的贡献表,发现是个斜杨辉三角
只有组合数为奇数才用贡献,由Lucas可知组合数C(n,m)为奇数等价于(n&m)==m
这样就可以枚举m(1~n-1)快速更新答案
虽然复杂度看上去是O(n^2),但是满足要求的组合数并不多(不会证明。。),能过
代码(解法一):
#include<bits/stdc++.h>
const int N = 2e5+10;
using namespace std;
int A[N],ans[N];
inline bool check(int n,int m){return (n&m)==m;}
int main(){
int T;
scanf("%d",&T);
while(T--){
int n,m;
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++){
scanf("%d",&A[i]);
ans[i] = A[i];
}for(int d=1;d<n;d++)if(check(m+d-1,d))
for(int i=d+1;i<=n;i++)ans[i] ^= A[i-d];
for(int i=1;i<=n;i++)printf("%d%c",ans[i],i<n?' ':'\n');
}return 0;
}
解法二:
思路来源:点击打开博客
打表的时候很容易发现运算规则:
多推几轮发现会两两相抵,可以得到式子:
那么总复杂度为O(n*log(n))
代码(解法二):
#include<bits/stdc++.h>
const int N = 2e5+10;
using namespace std;
int dp[N];
int main()
{
int T,n,m;
scanf("%d",&T);
while(T--){
scanf("%d%d",&n,&m);
for(int i=0;i<n;i++)scanf("%d",&dp[i]);
int k = 1 , ed = min(m+1,n);
while(k<ed){
if(k&m)for(int i=k;i<n;i++)dp[i]^=dp[i-k];
k<<=1;
}for(int i=0;i<n;i++)printf("%d%c",dp[i],i<n-1?' ':'\n');
}return 0;
}










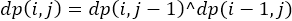
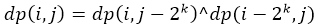














 531
531

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








