动态规划算法

问题描述：给定n个矩阵：A1,A2,...,An，其中Ai与Ai+1是可乘的，i=1，2...，n-1。确定计算矩阵连乘积的计算次序，使得依此次序计算矩阵连乘积需要的数乘次数最少。输入数据为矩阵个数和每个矩阵规模，输出结果为计算矩阵连乘积的计算次序和最少数乘次数。

问题解析：由于矩阵乘法满足结合律，故计算矩阵的连乘积可以有许多不同的计算次序。这种计算次序可以用加括号的方式来确定。若一个矩阵连乘积的计算次序完全确定，也就是说该连乘积已完全加括号，则可以依此次序反复调用2个矩阵相乘的标准算法计算出矩阵连乘积。

       完全加括号的矩阵连乘积可递归地定义为：

     （1）单个矩阵是完全加括号的；

     （2）矩阵连乘积A是完全加括号的，则A可表示为2个完全加括号的矩阵连乘积B和C的乘积并加括号，即A=(BC)

       例如，矩阵连乘积A1A2A3A4有5种不同的完全加括号的方式：(A1(A2(A3A4)))，(A1((A2A3)A4))，((A1A2)(A3A4))，((A1(A2A3))A4)，(((A1A2)A3)A4)。每一种完全加括号的方式对应于一个矩阵连乘积的计算次序，这决定着作乘积所需要的计算量。

      看下面一个例子，计算三个矩阵连乘{A1，A2，A3}；维数分别为10*100 , 100*5 , 5*50 按此顺序计算需要的次数((A1*A2)*A3):10X100X5+10X5X50=7500次，按此顺序计算需要的次数(A1*(A2*A3)):10*5*50+10*100*50=52500次

      所以问题是：如何确定运算顺序，可以使计算量达到最小化。      

 算法思路：

      例：设要计算矩阵连乘乘积A1A2A3A4A5A6，其中各矩阵的维数分别是：

A1	A2	A3	A4	A5	A6
30*35	35*15	15*5	5*10	10*20	20*25

递推关系：

      设计算A[i:j]，1≤i≤j≤n，所需要的最少数乘次数m[i,j]，则原问题的最优值为m[1,n]。

      当i=j时，A[i:j]=Ai，因此，m[i][i]=0，i=1,2,…,n
      当i<j时，若A[i:j]的最优次序在Ak和Ak+1之间断开，i<=k<j,则：m[i][j]=m[i][k]+m[k+1][j]+pi-1pkpj。由于在计算是并不知道断开点k的位置，所以k还未定。不过k的位置只有j-i个可能。因此，k是这j-i个位置使计算量达到最小的那个位置。

      综上，有递推关系如下：

          

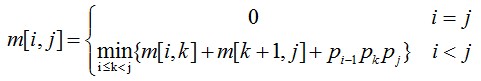
构造最优解：

      若将对应m[i][j]的断开位置k记为s[i][j]，在计算出最优值m[i][j]后，可递归地由s[i][j]构造出相应的最优解。s[i][j]中的数表明，计算矩阵链A[i:j]的最佳方式应在矩阵Ak和Ak+1之间断开，即最优的加括号方式应为(A[i:k])(A[k+1:j)。因此，从s[1][n]记录的信息可知计算A[1:n]的最优加括号方式为(A[1:s[1][n]])(A[s[1][n]+1:n])，进一步递推，A[1:s[1][n]]的最优加括号方式为(A[1:s[1][s[1][n]]])(A[s[1][s[1][n]]+1:s[1][s[1][n]]])。同理可以确定A[s[1][n]+1:n]的最优加括号方式在s[s[1][n]+1][n]处断开...照此递推下去，最终可以确定A[1:n]的最优完全加括号方式，及构造出问题的一个最优解。

      1、穷举法

      列举出所有可能的计算次序，并计算出每一种计算次序相应需要的数乘次数，从中找出一种数乘次数最少的计算次序。

      对于n个矩阵的连乘积，设其不同的计算次序为P(n)。每种加括号方式都可以分解为两个子矩阵的加括号问题：(A1...Ak)(Ak+1…An)可以得到关于P(n)的递推式如下：

      

      以上递推关系说明，P(n)是随n的增长呈指数增长的。因此，穷举法不是一个多项式时间复杂度算法。

      2、重叠递归

//A1 30*35 A2 35*15 A3 15*5 A4 5*10 A5 10*20 A6 20*25  
//p[0-6]={30,35,15,5,10,20,25}  
#include "stdafx.h"  
#include <iostream>   
using namespace std;   
  
const int L = 7;  
  
int RecurMatrixChain(int i,int j,int **s,int *p);//递归求最优解  
void Traceback(int i,int j,int **s);//构造最优解  
  
int main()  
{  
    int p[L]={30,35,15,5,10,20,25};  
  
    int **s = new int *[L];  
    for(int i=0;i<L;i++)    
    {    
        s[i] = new int[L];    
    }   
  
    cout<<"矩阵的最少计算次数为："<<RecurMatrixChain(1,6,s,p)<<endl;  
    cout<<"矩阵最优计算次序为："<<endl;  
    Traceback(1,6,s);  
    return 0;  
}  
  
int RecurMatrixChain(int i,int j,int **s,int *p)  
{  
    if(i==j) return 0;  
    int u = RecurMatrixChain(i,i,s,p)+RecurMatrixChain(i+1,j,s,p)+p[i-1]*p[i]*p[j];  
    s[i][j] = i;  
  
    for(int k=i+1; k<j; k++)  
    {  
        int t = RecurMatrixChain(i,k,s,p) + RecurMatrixChain(k+1,j,s,p) + p[i-1]*p[k]*p[j];  
        if(t<u)  
        {  
            u=t;  
            s[i][j]=k;  
        }  
    }  
    return u;  
}  
  
void Traceback(int i,int j,int **s)  
{  
    if(i==j) return;  
    Traceback(i,s[i][j],s);  
    Traceback(s[i][j]+1,j,s);  
    cout<<"Multiply A"<<i<<","<<s[i][j];  
    cout<<" and A"<<(s[i][j]+1)<<","<<j<<endl;  

     3、动态规划实现    

//3d1-2 矩阵连乘 动态规划迭代实现  
//A1 30*35 A2 35*15 A3 15*5 A4 5*10 A5 10*20 A6 20*25  
//p[0-6]={30,35,15,5,10,20,25}  
#include "stdafx.h"  
#include <iostream>   
using namespace std;   
  
const int L = 7;  
  
int MatrixChain(int n,int **m,int **s,int *p);   
void Traceback(int i,int j,int **s);//构造最优解  
  
int main()  
{  
    int p[L]={30,35,15,5,10,20,25};  
  
    int **s = new int *[L];  
    int **m = new int *[L];  
    for(int i=0;i<L;i++)    
    {    
        s[i] = new int[L];  
        m[i] = new int[L];  
    }   
  
    cout<<"矩阵的最少计算次数为："<<MatrixChain(6,m,s,p)<<endl;  
    cout<<"矩阵最优计算次序为："<<endl;  
    Traceback(1,6,s);  
    return 0;  
}  
  
int MatrixChain(int n,int **m,int **s,int *p)  
{  
    for(int i=1; i<=n; i++)  
    {  
        m[i][i] = 0;  
    }  
    for(int r=2; r<=n; r++) //r为当前计算的链长（子问题规模）    
    {  
        for(int i=1; i<=n-r+1; i++)//n-r+1为最后一个r链的前边界    
        {  
            int j = i+r-1;//计算前边界为r，链长为r的链的后边界    
  
            m[i][j] = m[i+1][j] + p[i-1]*p[i]*p[j];//将链ij划分为A(i) * ( A[i+1:j] )   
  
            s[i][j] = i;  
  
            for(int k=i+1; k<j; k++)  
            {  
                //将链ij划分为( A[i:k] )* (A[k+1:j])     
                int t = m[i][k] + m[k+1][j] + p[i-1]*p[k]*p[j];  
                if(t<m[i][j])  
                {  
                    m[i][j] = t;  
                    s[i][j] = k;  
                }  
            }  
        }  
    }  
    return m[1][L-1];  
}  
  
void Traceback(int i,int j,int **s)  
{  
    if(i==j) return;  
    Traceback(i,s[i][j],s);  
    Traceback(s[i][j]+1,j,s);  
    cout<<"Multiply A"<<i<<","<<s[i][j];  
    cout<<" and A"<<(s[i][j]+1)<<","<<j<<endl;  
}  

    4、备忘录方法

//3d1-2 矩阵连乘 备忘录递归实现  
//A1 30*35 A2 35*15 A3 15*5 A4 5*10 A5 10*20 A6 20*25  
//p[0-6]={30,35,15,5,10,20,25}  
#include "stdafx.h"  
#include <iostream>   
using namespace std;   
  
const int L = 7;  
  
int LookupChain(int i,int j,int **m,int **s,int *p);  
int MemoizedMatrixChain(int n,int **m,int **s,int *p);  
  
void Traceback(int i,int j,int **s);//构造最优解  
  
int main()  
{  
    int p[L]={30,35,15,5,10,20,25};  
  
    int **s = new int *[L];  
    int **m = new int *[L];  
    for(int i=0;i<L;i++)    
    {    
        s[i] = new int[L];  
        m[i] = new int[L];  
    }   
  
    cout<<"矩阵的最少计算次数为："<<MemoizedMatrixChain(6,m,s,p)<<endl;  
    cout<<"矩阵最优计算次序为："<<endl;  
    Traceback(1,6,s);  
    return 0;  
}  
  
int MemoizedMatrixChain(int n,int **m,int **s,int *p)  
{  
    for(int i=1; i<=n; i++)  
    {  
        for(int j=1; j<=n; j++)  
        {  
            m[i][j]=0;  
        }  
    }  
    return LookupChain(1,n,m,s,p);  
}  
  
int LookupChain(int i,int j,int **m,int **s,int *p)  
{  
    if(m[i][j]>0)  
    {  
        return m[i][j];  
    }  
    if(i==j)  
    {  
        return 0;  
    }  
  
    int u = LookupChain(i,i,m,s,p) + LookupChain(i+1,j,m,s,p)+p[i-1]*p[i]*p[j];  
    s[i][j]=i;  
    for(int k=i+1; k<j; k++)  
    {  
        int t = LookupChain(i,k,m,s,p) + LookupChain(k+1,j,m,s,p) + p[i-1]*p[k]*p[j];  
        if(t<u)  
        {  
            u=t;  
            s[i][j] = k;  
        }  
    }  
    m[i][j] = u;  
    return u;  
}  
  
void Traceback(int i,int j,int **s)  
{  
    if(i==j) return;  
    Traceback(i,s[i][j],s);  
    Traceback(s[i][j]+1,j,s);  
    cout<<"Multiply A"<<i<<","<<s[i][j];  
    cout<<" and A"<<(s[i][j]+1)<<","<<j<<endl;  
}  

    5、分析

    用算法RecurMatrixChain(1,4,s,p)计算a[1:4]的计算递归树如下图所示：

      从上图可以看出很多子问题被重复运算。可以证明，该算法的计算时间T(n)有指数下界。设算法中判断语句和赋值语句为常数时间，则由算法的递归部分可得关于T(n)的递归不等式：

     用数学归纳法可以证明，因此，算法RecurMatrixChain的计算时间也随n指数增长。

     6、结果