直方图均衡化
一个灰度分布不均匀的图像 它的直方图


可以看出,直方图上灰度集中在60周围,整个图像对比度较差,通过直方图均衡化,即可将其灰度均匀分布各个灰度级,从而使得图像具有更好的对比,增强图像细节。


均衡化后图像 均衡化后的直方图
1.问题分析
设随机变量x,y分别是均衡化前后的灰度取值,存在一个转换关系y=T(x)。
p(x),p(y)分别是x,y的概率密度函数。以p(x)为例,可以理解成,原图像灰度值是x的概率为多少。根据概率论相关知识,这里p(x)其实就是指 灰度值为x的像素数/总像素数,即该灰度值的出现概率,取值范围[0~1],同理得p(y)。(一开始我是用f(x),f(y)表示,为了表明它是一个概率,所以这样还是用p(x),p(y)代替)
p(x)是已知的。
p(y)是直方图均衡化得到的概率密度函数,在前面我们已经说了,希望能均衡化后的直方图,拥有跟高的对比度,灰度分布更均匀,所以理想状态中的分布均匀的直方图是这样的

这是理想中的直方图分布,这时每个灰度级的概率p=1/(L-1),就是p(y)=1/(L-1) L是灰度级数量,例如常用的L=256,灰度范围就是【0~255】
我们既然希望通过x计算出形如上面灰度分布的y,就需要求T(x)这个转换关系。这样,问题转变为:
已知p(x)和p(y),求T(x)。 问题【1】
2.公式推导
已知两个概率密度函数p(x),p(y),求x,y之间的转换关系T(x)。
这里,为了方便进行一般化情况的推导,我们将x视为一个连续的随机变量(实际上灰度值x肯定不是连续随机变量,但是为了进行公式推导和证明,先证明连续型随机变量成立,再引出离散型随机变量的情况),y就是随机变量x的函数。
概率论里有一个小章节,叫“随机变量的函数的概率分布”,应该所有版本的概率论与数理统计都有这个内容。在这个部分所求解的问题是:
已知p(x),x与y之间的转换关系T(x),求p(y)。 问题【2】
这两个问题本质上都是建立的三者之间的关系,通过两个已知量即可推导第三个量。现在我们只需要去求解问题【2】,然后就可以得到三者之间的关系式,带入p(x),p(y)就可以得到问题【1】的解。
问题【2】,p(y)证明过程,出自《概率论与数理统计》-陈希孺版:


逐步推导 :
x是随机变量,y=T(x),则y是随机变量x的函数,求解随机变量函数的概率密度,一般是通过求该函数的分布函数,对
分布函数求导,得到概率密度函数。
(我去看了几个概率论的视频,老师都是说这是一般求法,我还在想为啥非得要从分布函数入手,后来贴吧大神回答说应该去看一下概率密度函数的定义,然后我看了一下书,赫然有如下定义:)

求y的分布函数F(y),根据分布函数定义

所以F(y)=P(Y<=y),下面是后续推导过程
(1). ∵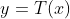 ,所以
,所以
∴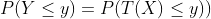
(2). T(x)有反函数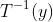 。反函数存在的充要条件:
。反函数存在的充要条件:
一个函数的定义域若是一个区间,则该函数存在反函数的充要条件是函数在定义域内严格单调。
T(x)是严格单调的吗?是的。我们不希望改变灰度值x的变换后的大小顺序,假如 x=50时,y=T(50)=20,当x=51,y=T(51),y一定是>20的。因为我们必须保证,直方图均衡化后,图像的明暗关系不能改变,原本最暗的像素点,可以变亮,但是在新图像里,它也应该是相对最暗的像素点。所以T(x)必须是一个严格单调的图像(在这里进一步说,对于图像,应该是严格单调递增的。)
∵ 存在反函数
存在反函数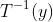
∴
这一步的转换, 最终变成了
最终变成了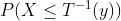 ,根据前面分布函数的定义可知,
,根据前面分布函数的定义可知, 是Y的分布函数F(y),
是Y的分布函数F(y),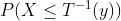 是X的分布函数,而在问题【2】的条件里,我们是不知道p(y),更不知道F(y)的,所以才要转换成F(x)
是X的分布函数,而在问题【2】的条件里,我们是不知道p(y),更不知道F(y)的,所以才要转换成F(x)
{
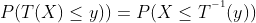 这一步,通过反函数将T(X)<=y转换为X<=T-1(y),将限制条件进行了转换
这一步,通过反函数将T(X)<=y转换为X<=T-1(y),将限制条件进行了转换
我对于反函数转换不太理解,看了好几个公开课视频,例如概率论与数理统计——清华大学(国家级精品课),这里面压根没提这个转换,到这直接跳了。我看了一会,这个系列视频讲得都很浅,应付考试差不多。
在 概率论与数理统计(中科大_缪柏其教授_33讲全) 里面,完整的讲了一下,老师讲得还是很全,但是反函数变换这一步还是没细讲。
最后在 武汉理工大学《概率论与数理统计》全52讲 这一章节,老师画了个坐标系,一下子就理解了。
![]()
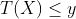 ,就是指图中红色部分线段,图中唯一的点(x,y),根据反函数,
,就是指图中红色部分线段,图中唯一的点(x,y),根据反函数,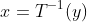 ,这里
,这里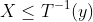 所代表的线段范围,就是
所代表的线段范围,就是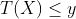 的范围,即
的范围,即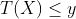 与
与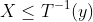 等价,所以
等价,所以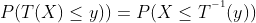 (这里成立的条件是T(x)单调递增,这样不等号不用变号,单调递减要变号)
(这里成立的条件是T(x)单调递增,这样不等号不用变号,单调递减要变号)
}
(3). 转换成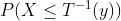 后,这个形式就是对X求积分,积分上限为
后,这个形式就是对X求积分,积分上限为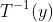
∴ 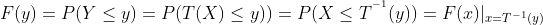
这时候,我们把y的分布函数和x的分布函数联系起来了
(4). 上式还可以进一步写成
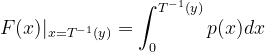
则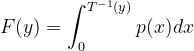 ,两边同时对y求导,根据变上限积分的求导法则
,两边同时对y求导,根据变上限积分的求导法则

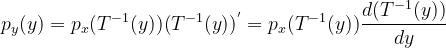 (这里改成
(这里改成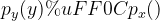 主要是为了区分x,y的概率密度函数)
主要是为了区分x,y的概率密度函数)
∵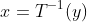
∴
这样就得到了很多介绍直方图均衡化的博客中,直接引用的公式,r,s分别指直方图均衡化前后的灰度值

我们推导得到的没有绝对值符号,是由于dx/dy一定>0,因为y=T(x)单调递增。
(5). 带入值
∵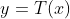
∴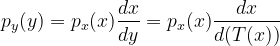
这里,得到了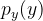 的表达式,问题【2】求解步骤就可以终止了,因为已知了
的表达式,问题【2】求解步骤就可以终止了,因为已知了 ,,将已知变量带入,经过变换
,,将已知变量带入,经过变换
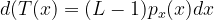
为了求解T(x),两边同时对x积分,由于积分和微分互为逆运算
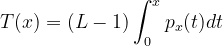 这里把
这里把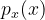 写成
写成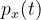 只是为了把变量跟积分上限x区分,被积函数还是x的概率密度
只是为了把变量跟积分上限x区分,被积函数还是x的概率密度
(6) 注意,现在得到的是连续型随机变量的T(x)计算公式,由于x是一个离散变量,对离散变量积分,就是求和
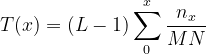
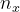 是灰度值为x时的像素点数量,M*N是图像的长宽积,即总像素数量。
是灰度值为x时的像素点数量,M*N是图像的长宽积,即总像素数量。
∵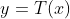
∴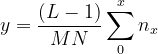
至此,计算出直方图均衡化所需的转换公式,还有需要注意的一点,
为了保证直方图均衡化后图像灰度是均匀分布,我们假定了像素点落到每个灰度级的概率是完全相等的
所以理论上直方图是一条直线。但是由于实际图像是离散的,且不能保证原图像在每个灰度值x都有值,所以均衡化后的直方图只是往理论直方图靠近,随着点数增多,灰度级分布才会越来越接近均匀。(未证明)
3.结束
作为一个工科出身转的视觉方向,基础薄弱,对于大部分处理方法都是限于会使用,明白大概原理,少部分算法在上学时进行过推敲。加上工作两年了,对于图像处理这块越来越陷入应用,完全依赖商用开发包,对于自己吃饭家伙的理解,越来越流于表面。今年重写公司的一些标准工具时候,决心从头开始理解推导,哪怕是重复造轮子,也得手动再来一遍。
本科4年唯一挂掉的课就是概率论,现在还记得当年全院500多人,总共挂了二三十号人,我以56分高高挂起。加上本书数学基础差,考研又是全院数学最低分,跟学校的数学最低分数线一样,数学跟英语考得一样,如果不是其他三门给了点力,就完蛋了。
所以,写这篇博客用了三天,重新学习了数学基础知识,发现自己真是所有东西都快忘完了,连分布函数和概率密度的定义都忘了。
水平有限,本文多有疏漏,反正推理过程能说服我自己就行了。
主要参考博客:
https://blog.csdn.net/spongebob1234/article/details/77778709(这个写的还是非常直观,话不多但是都是写了关键地方。)
https://blog.csdn.net/schwein_van/article/details/84336633
参考书籍
概率论与数理统计 陈希孺(这本书真的很不错, 我们当年用的书是本校自己写的,内容非常浅显而且僵硬,没有老师讲很难理解的了)
























 910
910

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








