求一个无序数组中第K小问题

这种问题如果先排序，那么至少时间复杂度为O(nlogn)

但是有种方法可以达到O(n)

这种方法有个阙值，只有大于44的时候用这种方法才比先排序后查找的快

首先上一段伪代码吧

if(N<44) then 排序A return A[K];   ---O(1)
else 
	i <- [N/5] 将数组分成五个元素一小组，一共N/5组  ---O(N)
排序这个5个元素的数组，找到这个N/5组中每组的中间项 组成一个集合S ---O(N)
m <- select(S,N/5,(N/5)/2) 找到这个集合中的中间项m  --T(N/5)

B = { a | a < m } 
C = { a | a = m }          ---O(N)
D = { a | a > m }  

if(k<B.length) then return select(B,B.length,k) 
else	
	if(k<B.length+C.length) return m
	if(K>B.length+C.length) return select(D,D.length,k-B.length-C.length)

分析下select算法在最坏的情况下的时间复杂度
唯一难以判别的情况只有最后一部分代码，其他部分的代码的时间复杂度都能很轻易的看出
想确定最后一部分代码的时间复杂度先确定问题规模，也就是那三个集合BCD的规模
因为m为中位数，N/5个数组也排序了，可以将其分成四组+1个点 最坏的情况下，有三组是小于m数的也就是B集合
这三组是有两组只取N/5个数组中的两个元素，有一个取3个，那么相对于原问题N的规模是7/10
也就是说 W(n) = w(n/5) + w(7/10) + cn 然后用递归树解一下，得到O(N)

上面的文字说明有点玄乎，没关系我还特意画了图

以下都是假设最坏的情况

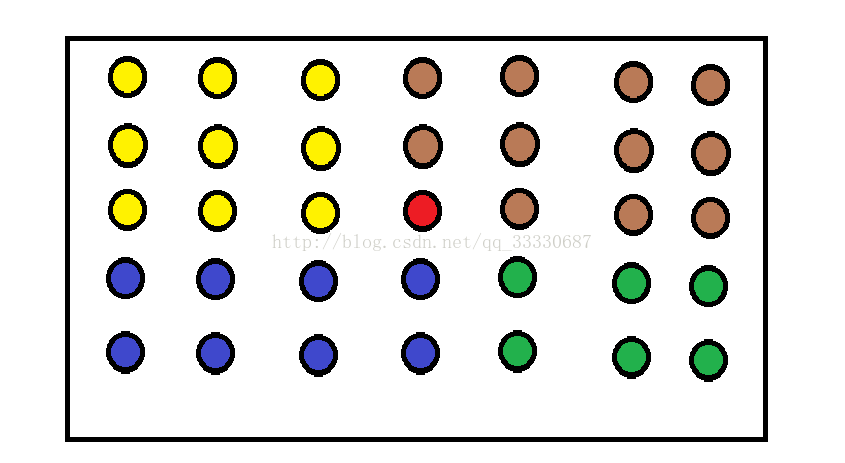
红色的就是我们求的那个m，也就是将数组划分N/5个小数组后每个小数组排好序，取中间项组成的集合S当作的中间项

然后红色哪一行，从左到右是升序

这图当中从上到下是依次减小的！！！！！

然后我们假设黄色+蓝色+绿色都是比红色小的，这种情况是存在的吧，没毛病吧？

然后我们算下黄色+蓝色+绿色的范围（规模）是多大

为了研究问题方便，然后我们近似的认除了红色的其他四个颜色区域列数相等，（在研究N规模问题的时候是没有问题的，相别不是很大，只有红色上面下面两个数的差别可以忽略）

2r = 蓝色

2r = 绿色

3r = 黄色

3r = 棕色

2r + 2r + 3r + 3r = N

5个数，不同色所在的比例不一样，不是占3个就是占2个

全部颜色加起来就是N个元素

很明显可以得到上面的结论

所以黄色+蓝色+绿色是占全部的7N/10

那么很明显了W(n) <<= w(n/5) + w(7n/10) + cn

得到O(N)

下面给出一个java版本的实现，简单实现

	
	/**
	 * return Nth small integer in this array
	 * @param array an integer array
	 * @param length length of this integer array
	 * @param index Nth
	 * @return number of Nth small integer in this array
	 */
	public static int select(ArrayList<Integer> array,	int length,	int index){
		
		if(length<44){
			Collections.sort(array);
			return array.get(index-1);
		}
		
		int i = length/5;
		ArrayList<Integer> S =  new ArrayList<>(i);
		int j = 1;
		while(j<=i){
			int k = (j-1)*5;
			int[] n = new int[5];
			n[0] = array.get(k);
			n[1] = array.get(k+1);
			n[2] = array.get(k+2);
			n[3] = array.get(k+3);
			n[4] = array.get(k+4);
			Arrays.sort(n);
			S.add(n[2]);
			j++;
		}
		
		int m = select(S,i,i/2);
		
		ArrayList<Integer> less = new ArrayList<>();
		ArrayList<Integer> equal = new ArrayList<>();
		ArrayList<Integer> more = new ArrayList<>();
		
		for(int idx = 0;idx<array.size();idx++){
			if(array.get(idx)<m){
				less.add(array.get(idx));
			}else if(array.get(idx)==m){
				equal.add(array.get(idx));
			}else{
				more.add(array.get(idx));
			}
		}
	
		if(index<=less.size()){
			return select(less,less.size(),index);
		}else if(index<=less.size()+equal.size()){
			return m;
		}else
			return select(more,more.size(),index-less.size()-equal.size());
			
	}