数学建模——统计回归模型

前言：看完数学建模的统计回归模型，更是感到了数学建模的“细腻”之处，对比与机器学习，如果说机器学习像是“打一场仗”，那数学建模更是像“做一场手术”，一个简单的回归问题也可以从中感觉到他“细腻”的美感

回归模型是利用统计分析方法建立的最常用的一个模型，下面将通过对软件得到的结果进行分析，进而改进我们的模型。

下面将用3个例子展示对回归模型的优化。

1.牙膏的销售模型

问题的提出：假设一个公司需要预测不同价格和广告费用下的牙膏的销售量，我们需要怎么建立模型呢？

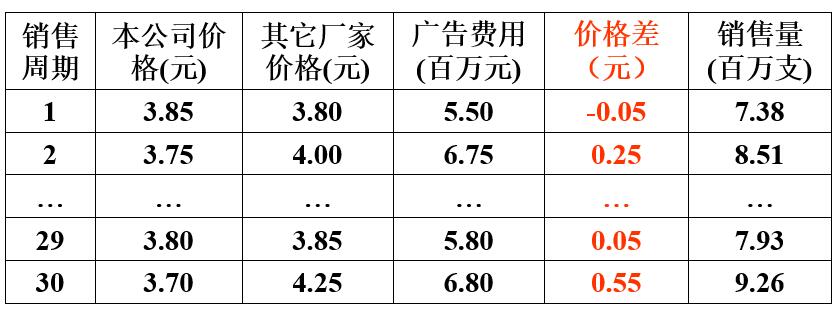
假设我们拿到的数据如下：

我们可以根据数据建立一个基本的模型：
$y：公司牙膏销售量$
$x_1：价格差$
$x_2：公司广告的费用$

模型为：$y=\beta_0 + \beta_1 x_1 +\beta_2 x_2+\beta_3 x_2^2 + \epsilon$

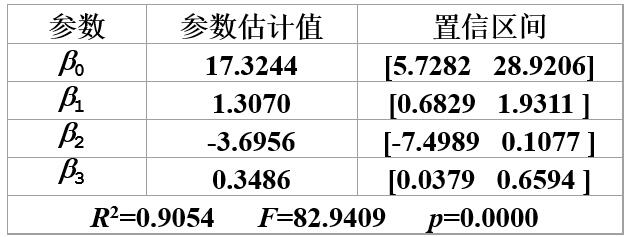
求解这个模型我们会得到下面的结果：

这说明y的90.54%可以由模型确定，x2对因变量y 的影响不太显著（因为$\beta_2 的置信区间包括0点$）。

这些数据具体到公司的销售量到底意味着什么呢？

假设我们把控制价格差$x_1=0.2$，投入广告费$x_2=650$万，根据我们的模型可以求出y的值为8.2933（百万支），销售量的预测区间为[7.8230，8.7636]。

那么我们就有95%把握知道销售量在7.8320百万支以上。

优化——加入交互项

刚才我们只考虑了每个因素单独的影响，现在我们考虑他们的影响有交互作用，即我们的模型变为：