COMSOL有限元仿真偏振光成像

已于 2024-07-27 20:13:11 修改
阅读量745 收藏
点赞数 2
文章标签： 经验分享 远程工作 设计模式
于 2024-07-27 17:06:52 首次发布
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/qq_33440209/article/details/140738117
版权

仿真内容:偏振光成像
1、软件要求:COMSOL6.2
2、仿真目标
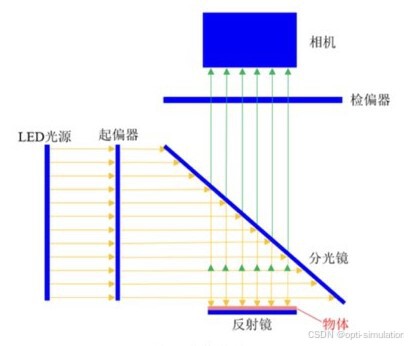
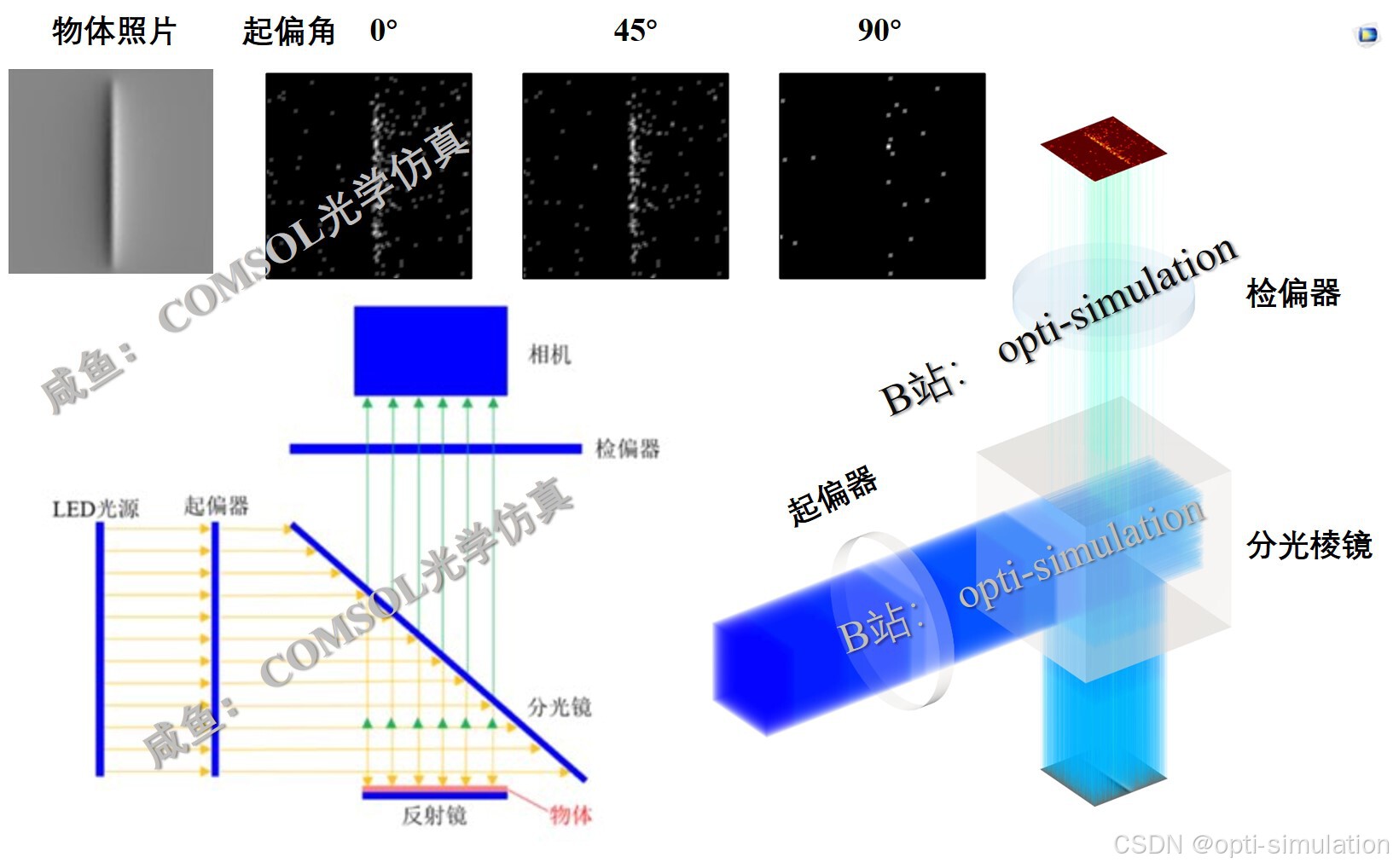
通过图1所示偏振光成像光路，对图2所示物体成像，具体光路描述如下:

a)LED光源发出平行均匀自然光，自然光经过起偏器变为线偏振光;
b)线偏振光被分光镜(半透半反镜)反射(黄色箭头示意)，穿过透明的物体，进入反射镜被反射:c)被反射的光线(绿色箭头示意)穿过分光镜，然后再经过检偏器进入相机，从而完成相机对物体的成像

咸鱼主页：COMSOL光学仿真

B站主页：opti-simulation的个人空间-opti-simulation个人主页-哔哩哔哩视频 (bilibili.com)

光学系统仿真软件：OSLO_（12）.偏振光学仿真
kkchenjj的博客
04-11 866
偏振光的仿真在光学系统的设计和优化中起着至关重要的作用。从简单的线偏振光到复杂的椭圆偏振光，再到多个偏振元件的组合，OSLO库提供了丰富的工具和方法来实现这些仿真。通过分析和优化偏振光的特性，可以提高光学系统的性能，减少信号失真，提高传输效率和成像质量。在实际应用中，偏振光的控制和仿真对于光纤通信、成像系统、干涉仪和激光加工等领域具有重要意义。希望本文能为读者提供一个全面的偏振光仿真入门指南。
多物理场光学仿真软件：COMSOL_（5）.波动光学仿真
kkchenjj的博客
04-02 674
使用“几何”（Geometry）工具创建所需的几何模型。例如，创建一个矩形区域表示光波导。
comsol的光学模型
09-10
comsol的光学模型，包括图片和模型程序，图片详细介绍了每个参数的设置方法和数据。
COMSOL声学（线下）-光电（线上），几十种案例仿真
xiaoxiaoxiaolll的博客
08-24 751
Ø 散射边界和端口边界的使用方法和技巧（波失方向和极化方向设置、S参数、反射率和透射率的计算和提取、高阶衍射通道反射投射效率的计算）初识COMSOL仿真——以多个具体的案例建立COMSOL仿真框架，建立COMSOL仿真思路，熟悉软件的使用方法。初识COMSOL仿真——以多个具体的案例建立COMSOL仿真框架，建立COMSOL仿真思路，熟悉软件的使用方法。Ø COMSOL WITH MATLAB 进行复杂的物理场或者集合模型的建立(如超表面波前的衍射计算)
comsol—偏振光仿真
funan_jiachun的博客
04-24 8786
光矢量的振动方向在传播过程中保持不变，只是它的大小随位相改变，这种光称为线偏振光 圆偏振光的特点是，在传播过程中，它的光矢量大小不变，方向绕传播轴均匀地转动，端点轨迹是一个圆。 椭圆偏振光的光矢量大小和方向在传播过程中都有规律地变化，光矢量端点沿着一个椭圆轨迹运动。 光在空间中传播的方程为 在直角坐标系中分解 我们在该例中设置传播方向沿x轴方向所以α=0°，β=γ=90° 接下来利用comsol对该现象进行仿真 选择模型三维>电磁波，频域(ewfd)>波..
comsol中圆偏振的设置
03-07
圆偏振光在comsol中的模拟，本模型是重复文献Circular Dichroism Metamirrors with Near-Perfect Extinction的结果，有需要的小伙伴可以下载使用
记录：COMSOL仿真——光子晶体光纤
热门推荐
k903161661的博客
09-29 2万+
使用COMSOL软件对光子晶体光纤进行一系列仿真
comsol仿真径向偏振光，角向偏振光
sByEkGKkFtR的博客
03-07 407
在这一领域，comsol仿真因其强大的功能和应用广泛性，得到了广泛的应用。今天，我们将围绕径向偏振光和角向偏振光的技术特性展开讨论，探讨其在仿真中的应用和优势。在径向偏振光与角向偏振光的仿真中，comsol提供了多种模块和工具，可以实现多种物理现象的模拟和分析。未来，随着技术的不断进步和创新，comsol仿真将会越来越完善和成熟，为各种光子器件和通信的设计和仿真提供更加便捷、高效的技术支持。在未来的研究和应用中，我们应该积极探索和应用这一技术，为各种光子器件和通信的设计和仿真提供更加便捷、高效的技术支持。
利用COMSOL模拟实现线偏振转换多重干涉效应
IGBrjKgxC的博客
06-09 645
在光纤通信、光码分多址等领域中，comsol线偏振转换多重干涉技术的应用已经取得了显著的效果，并且在未来的光通信系统中仍有广阔的发展前景。总之，comsol线偏振转换多重干涉技术作为一种重要的光学技术手段，在光通信领域中具有广泛的应用前景。在现代科技发展的背景下，光学技术作为一种重要的应用领域，其在信息传输、图像显示、光通信等领域中具有广阔的应用前景。线偏振转换是指将光波的偏振状态从一种形式转换为另一种形式的过程，其中包括线偏振光到圆偏振光、圆偏振光到线偏振光的转换。comsol线偏振转换多重干涉。
扭转光子晶体调节远场偏振，comsol直接出图
10-10
COMSOL Multiphysics是一种先进的多物理场仿真软件，它能够帮助科学家和工程师通过有限元分析的方法来模拟和优化光子晶体的设计。利用COMSOL软件直接出图，研究者可以直观地观察到不同参数下的偏振态分布和传播特性...
偏振光matlab仿真
04-22
光学偏振光“光密介质射入光疏介质时二向衰减系数随入射角的变化”matlab仿真
光学方面的仿真
07-13
有关光学和光学的matlab仿真，光学工程书籍
COMSOL光学仿真专题
05-13
关于光学的COMSOL仿真分析，可以作为参照的例子进行练习
光的偏振态仿真
12-18
对两相互垂直偏振态的合成进行计算，绘出电场的轨 迹。要求计算在=0、=/4、=/2、=3/4、=、=5/4、=3/2、=7/4时，在Ex=Ey及Ex=2Ey情况下的偏振态曲线并总结规律。
Comsol仿真中异常折射现象及折射角精确计算方法研究,Comsol异常折射与折射角精确求解 ,Comsol异常折射; 折射角精确求解; 光线传播; 光学仿真 ,"Comsol异常折射分析：精确求解
01-21
此外，对于复杂的光学系统，结合数值方法如有限元法进行仿真分析是必不可少的。在Comsol中，可以利用内置的物理场接口来进行这一工作，如电磁波、频域或射线光学模块等。 技术分析文档中提供的“异常折射与折射角...
光学仿真基础：COMSOL电磁波模块快速入门
[光学仿真基础：COMSOL电磁波模块快速入门](https://media.cheggcdn.com/media/895/89517565-1d63-4b54-9d7e-40e5e0827d56/phpcixW7X) # 摘要 光学仿真在现代光学设计与分析中扮演着关键角色，特别是在理解和预测...
基于Comsol技术的散射体手性研究,基于Comsol散射体特性分析手性现象,Comsol散射体手性 ,Comsol; 散射体; 手性; 电磁波散射; 散射特性,Comsol模拟中手性散射体的电磁特
03-01
Comsol技术是一种基于有限元分析方法的仿真软件，广泛应用于工程和物理科学领域的模拟。散射体手性研究则是电磁学中的一个分支，主要探讨手性物质在电磁波作用下的散射特性和电磁特性。手性是分子或物体的一种对称性...
基于Comsol散射体特性研究手性效应的探讨,Comsol散射体手性 ,核心关键词：Comsol；散射体；手性；模拟 ,"Comsol模拟中手性散射体的电磁特性研究"
01-26
Comsol Multiphysics是一款基于有限元分析的多物理场仿真软件，它能够模拟电磁场、流体动力学、结构力学等多种物理现象。在电磁波散射领域，Comsol可以帮助研究者模拟散射体在不同频率电磁波照射下的散射特性，这...
小孔成像仿真
最新发布
04-03
<think>好的，我现在需要帮助用户进行小孔成像的仿真。首先，用户的问题是关于小孔成像仿真的方法、工具或软件。根据用户提供的引用信息，我需要结合这些参考资料来给出合适的建议。 首先，查看用户提供的引用内容。引用[1]提到了基于Matlab的光学衍射仿真，特别是衍射实验的仿真。这可能是一个重要的资源，因为Matlab在科学计算和光学仿真方面有很强的能力，适合处理波动光学的问题，包括小孔衍射。引用[2]讨论了将光阑换成圆孔，并用平面波作为光源，这涉及到衍射的基本原理，可能与小孔成像相关。引用[3]和[4]似乎与理论物理和算法岗相关，可能对仿真的具体实现帮助不大，但引用[3]提到几何算法和3D重建，这可能在某些仿真方法中涉及几何光学部分。 接下来，我需要确定小孔成像仿真的主要方法。小孔成像通常涉及几何光学和波动光学两个层面。几何光学方面，可以用光线追踪的方法，模拟光线通过小孔后的传播路径，生成倒立实像。而波动光学则需要考虑光的波动性，如衍射效应，特别是当小孔尺寸与光波长相当时，衍射现象显著，此时需要基于惠更斯-菲涅耳原理进行模拟。 根据引用[1]，Matlab已经用于光学衍射仿真，可以处理波动光学中的衍射问题。这可能是一个关键工具。用户可能需要使用Matlab编写脚本，设置光源、小孔参数（如孔径大小、形状），然后应用衍射公式（如夫琅禾费衍射或菲涅耳衍射）进行计算，最后可视化结果。引用[2]中的圆孔衍射和圆屏衍射的比较，可能帮助用户理解不同孔径对成像的影响，这也需要波动光学的仿真。 另外，可能还有其他工具或软件，如COMSOL Multiphysics、Zemax等专业光学软件。COMSOL适用于多物理场仿真，包括光学；Zemax则主要用于光学系统设计，支持几何光学和衍射分析。Python的库如NumPy、SciPy和Matplotlib同样可以进行类似的仿真，特别是对于衍射计算，可能通过快速傅里叶变换（FFT）来实现，类似于Matlab的方法。 用户的需求可能分为两种情况：一种是希望进行基础的几何光学仿真，另一种是更复杂的包含衍射效应的仿真。如果是前者，光线追踪软件如POV-Ray或Blender可能足够；如果是后者，Matlab或Python结合科学计算库会更合适。 需要提醒用户注意小孔尺寸对成像的影响。当孔径较大时，几何光学近似有效，成像较清晰；当孔径接近波长量级时，衍射效应明显，成像模糊，需用波动光学方法。同时，仿真时需要设置正确的参数，如波长、孔径尺寸、光源类型（单色/多色、相干/非相干）以及像屏的位置。 最后，根据引用[1]和[2]，基于Matlab的仿真是可行且被验证过的方法，用户可以参考提供的文档进行具体实现。同时，如果用户更熟悉Python，也可以使用类似的数值计算库来完成。</think>### 小孔成像仿真方法与工具 小孔成像的仿真可通过几何光学或波动光学两种方式实现，具体方法及工具如下： --- #### **一、仿真方法** 1. **几何光学方法** - **原理**：模拟光线直线传播，小孔尺寸远大于光波长时适用。 - **步骤**： 1. 定义光源（如点光源或扩展光源）。 2. 设置小孔位置与孔径（如圆形、方形）。 3. 计算光线穿过小孔后的传播路径，生成倒立实像。 4. 可视化像屏上的光强分布。 2. **波动光学方法（含衍射效应）** - **原理**：基于惠更斯-菲涅耳原理，适用于小孔尺寸接近光波长的情况[^1]。 - **步骤**： 1. 使用夫琅禾费衍射或菲涅耳衍射公式计算光场分布。 2. 通过快速傅里叶变换（FFT）加速数值计算。 3. 分析像屏上的衍射图样（如艾里斑）。 --- #### **二、推荐工具与软件** 1. **Matlab** - **优势**：内置矩阵运算与FFT功能，适合波动光学仿真。 - **示例代码（夫琅禾费衍射）**： ```matlab lambda = 632.8e-9; % 波长（红光） d = 1e-4; % 小孔直径（100微米） z = 0.1; % 像屏距离（0.1米） [X,Y] = meshgrid(linspace(-5e-3,5e-3,500)); r = sqrt(X.^2 + Y.^2); aperture = (r < d/2); % 圆形孔径 U = fftshift(fft2(aperture)); % 衍射计算 I = abs(U).^2; % 光强分布 imshow(I/max(I(:))); % 显示结果 ``` - **参考**：Matlab光学衍射实验仿真文档[^1]。 2. **Python（NumPy/SciPy + Matplotlib）** - **优势**：开源灵活，代码与Matlab逻辑类似。 - **关键库**： ```python import numpy as np import matplotlib.pyplot as plt wavelength = 632.8e-9 d = 1e-4 z = 0.1 x = np.linspace(-5e-3, 5e-3, 500) y = np.linspace(-5e-3, 5e-3, 500) X, Y = np.meshgrid(x, y) r = np.sqrt(X**2 + Y**2) aperture = (r < d/2).astype(float) U = np.fft.fftshift(np.fft.fft2(aperture)) I = np.abs(U)**2 plt.imshow(I, cmap='gray') plt.show() ``` 3. **专业光学软件** - **COMSOL Multiphysics**：支持多物理场耦合，可模拟复杂衍射场景。 - **Zemax OpticStudio**：适用于光学系统级仿真，含几何与衍射分析模块。 --- #### **三、注意事项** 1. **孔径尺寸与波长关系**： - 当$d \gg \lambda$时，几何光学占主导，成像清晰。 - 当$d \sim \lambda$时，需考虑衍射效应，波动光学方法更准确[^2]。 2. **光源类型**：单色光/白光、相干/非相干光需区别建模。 3. **像屏分辨率**：高分辨率网格可捕捉更精细的衍射细节。 ---
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值