python绘制激活函数曲线图及其导数曲线图，激活函数包括sigmoid、relu、tanh

因写大论文需要，在知网上别人的论文中扣下来清晰度不够，其他网页上截屏下来可能包含水印，同时也比较难找全。因此参考CSDN博客资料，自己画出来用于论文书写。

import math
import numpy as np
import matplotlib.pyplot as plt

# set x's range
x = np.arange(-10, 10, 0.1)

y1 = 1 / (1 + math.e ** (-x))  # sigmoid
# y11=math.e**(-x)/((1+math.e**(-x))**2)
y11 = 1 / (2 + math.e ** (-x)+ math.e ** (x))  # sigmoid的导数

y2 = (math.e ** (x) - math.e ** (-x)) / (math.e ** (x) + math.e ** (-x))  # tanh
y22 = 1-y2*y2  # tanh函数的导数

y3 = np.where(x < 0, 0, x)  # relu
y33 = np.where(x < 0, 0, 1)  # ReLU函数导数

plt.xlim(-4, 4)
plt.ylim(-1, 1.2)

ax = plt.gca()
ax.spines['right'].set_color('none')
ax.spines['top'].set_color('none')
ax.xaxis.set_ticks_position('bottom')
ax.yaxis.set_ticks_position('left')
ax.spines['bottom'].set_position(('data', 0))
ax.spines['left'].set_position(('data', 0))

# Draw pic
plt.plot(x, y1, label='Sigmoid', linestyle="-", color="red")
plt.plot(x, y11, label='Sigmoid derivative', linestyle="-", color="violet")

plt.plot(x, y2, label='Relu', linestyle="-", color="blue")
plt.plot(x, y22, label='Relu derivative', linestyle="-", color="violet")

plt.plot(x, y3, label='Tanh', linestyle="-", color="green")
plt.plot(x, y33, label='Tanh derivative', linestyle="-", color="violet")



# Title
plt.legend(['Sigmoid', 'Tanh', 'Relu'])
plt.legend(['Sigmoid', 'Sigmoid derivative'])  # y1 y11
plt.legend(['Relu', 'Relu derivative'])  # y2 y22
plt.legend(['Tanh', 'Tanh derivative'])  # y3 y33

plt.legend(['Sigmoid', 'Sigmoid derivative', 'Relu', 'Relu derivative', 'Tanh', 'Tanh derivative'])  # y3 y33
# plt.legend(loc='upper left')  # 将图例放在左上角

# save pic
# plt.savefig('plot_test.png', dpi=100)
plt.savefig(r"./Desktop/to/SRL_result")

# show it!!
# plt.show()

根据个人需要，可以通过对代码的注释达到自己的要求。
贴图：




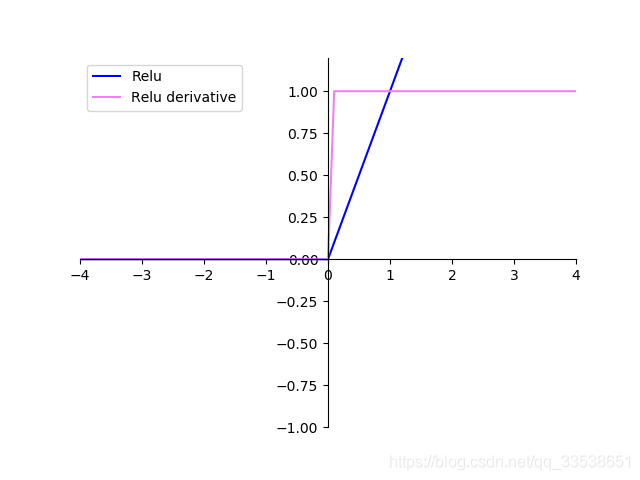
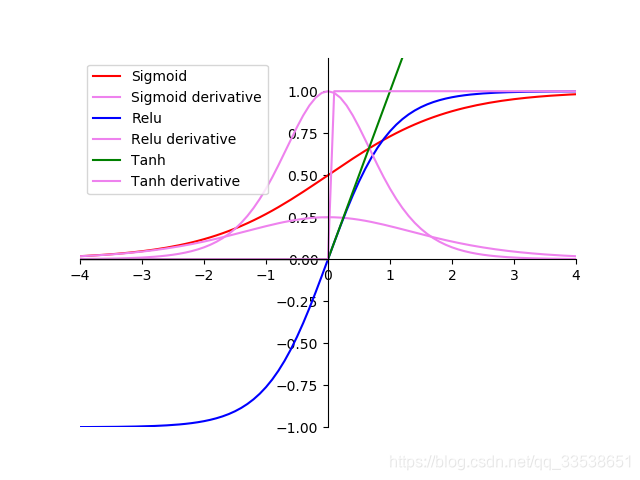
参考博客：
1.python绘制同时包含Sigmoid、Tanh和Relu函数的图像
https://blog.csdn.net/four_sea/article/details/89734991
2.激活函数-Sigmoid, Tanh及ReLU
https://blog.csdn.net/lwc5411117/article/details/83620184