更新:本网页为纯图片版,是由 Word 文档转图片后直接上传的。目前我已更新一个 Markdown 文字版的,网页浏览体验会好一些。因为一篇博客的字符数量有限制,所以分开了三篇。
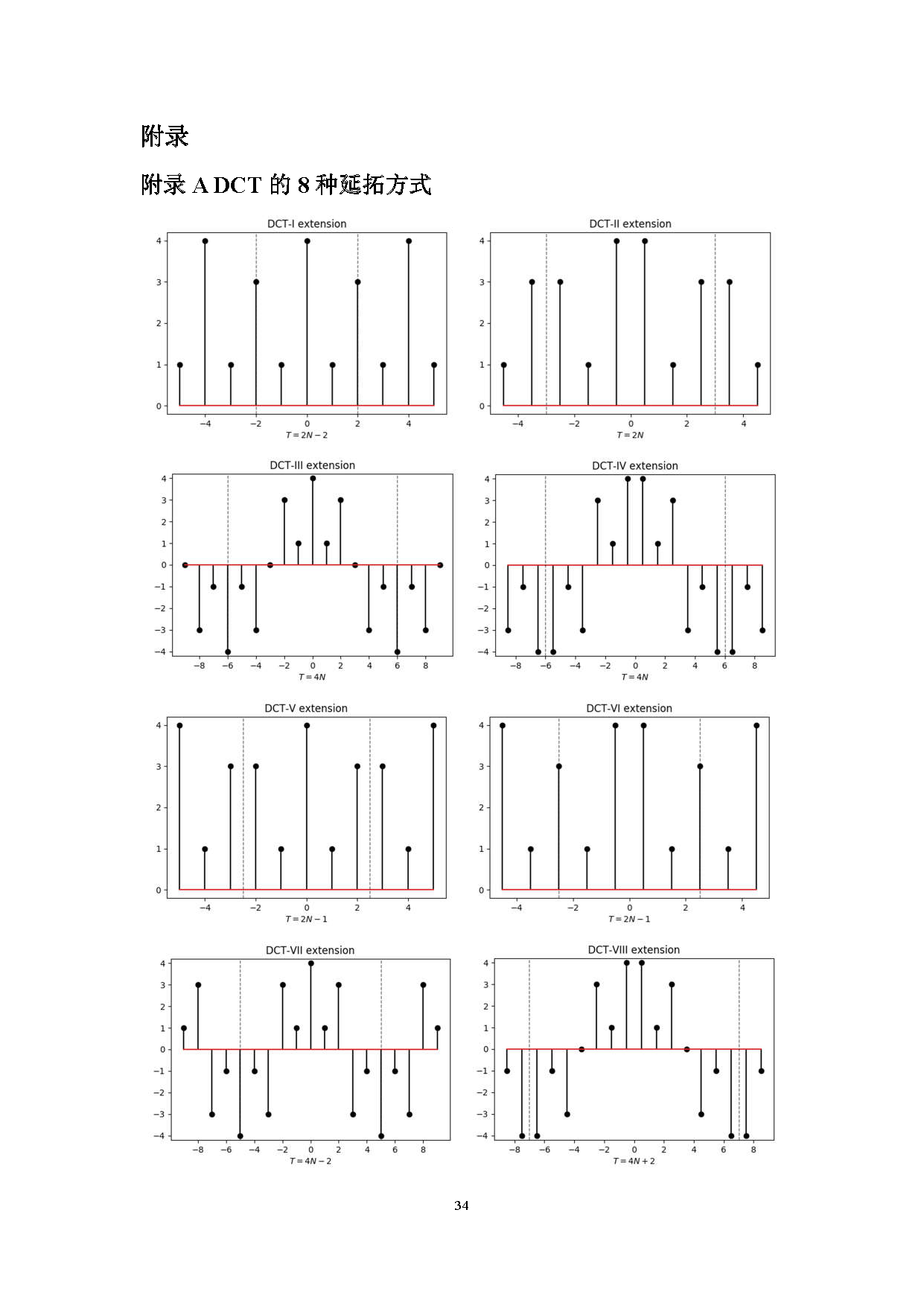
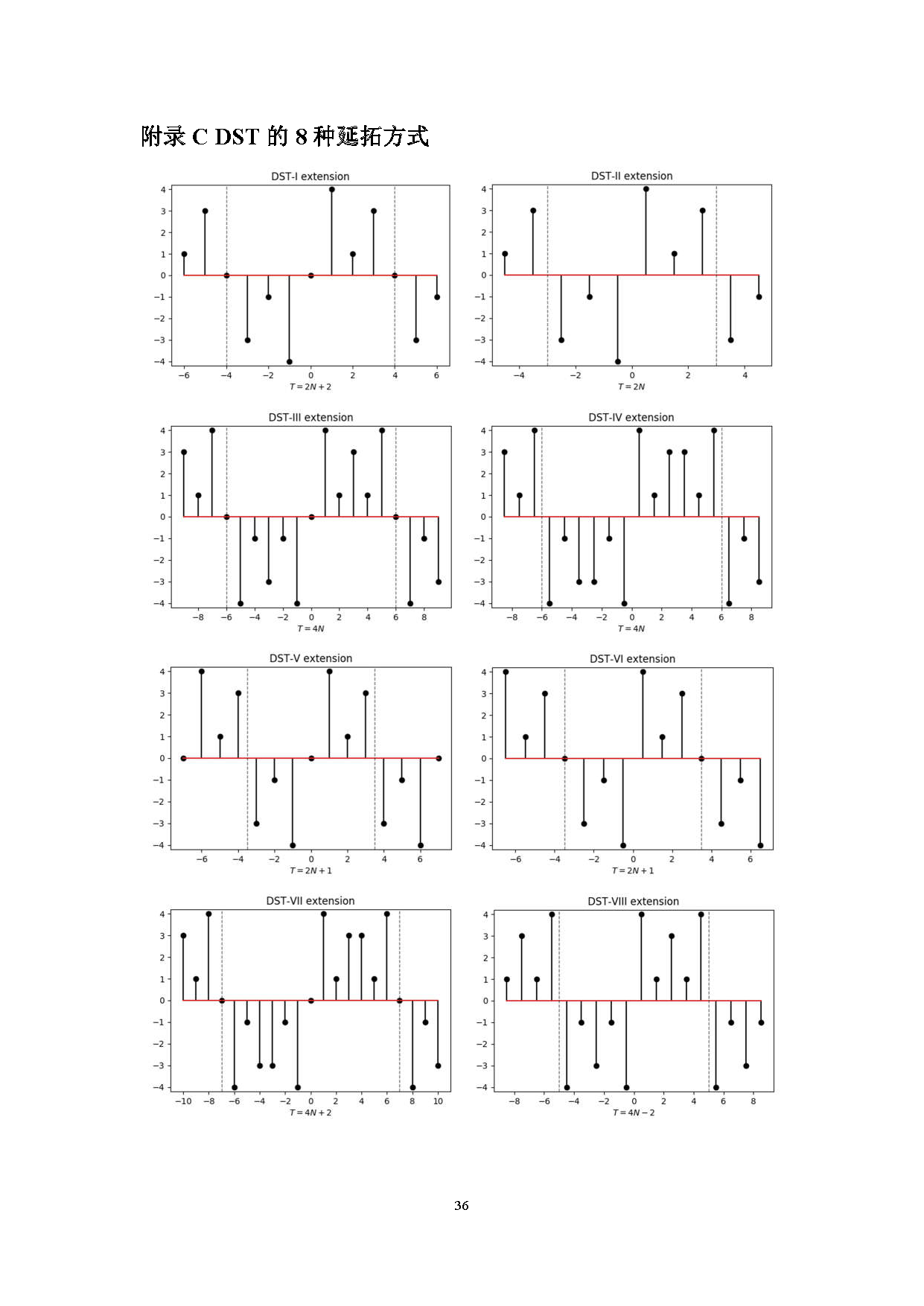
目前主流视频编解码算法都要使用到离散余弦变换(Discrete Cosine Transform)以及离散正弦变换(Discrete Sine Transform)对预测残差进行空域/频域的转换,通过牺牲部分高频的信息来达到压缩的目的。总的来说,DCT和DST都各自有八种形式,网上主要的资料都是介绍DCT-II,也就是第二类DCT,至于其他类型的资料少之又少,更不用说关于DST的介绍。过去,DCT-II由于其自身确实具有的优越性,在早期的编解码算法如H.264中大量使用,但后来人们发现其他的DCT和DST在某些情况下表现或许更加出色,例如,最新的H.266标准也将DCT-VIII以及DST-VII加入到了候选变换类型中。因此,为了弄懂H.266为什么要使用这三种变换类型,我们有必要对DCT和DST的原理做深入的理解。
很多人可能并不清楚DCT和DST从何而来,也不知道为什么它们两者为什么会有那么多种形式。实际上,DCT和DST的推导完完全全来自于离散傅里叶变换(Discrete Fourier Transform),他们两者本质上是DFT的特殊形式,因此,如果弄懂了DFT,DCT和DST也就自然理解了。所以,文章开始着重分析了DFT的一些性质,实际上是为后面做必要的铺垫。不过,要弄懂DFT,还要从傅里叶级数以及傅里叶变换说起,但由于篇幅限制,这里就不说了,大家可以找一些信号与系统的书籍资料学习一下,其实文章的内容大部分在那本绿皮的《数字信号处理》里面都有。因为这个文档我是写在Word里的,要转成Markdown不太方便,所以就直接转成图片了,后面篇幅比较长,但其实弄懂了前面的DFT后面的都只是一些重复性的工作而已。公式较多,内容较广,所以有些文字上的错误或者理解上的偏差在所难免。
离散傅里叶变换








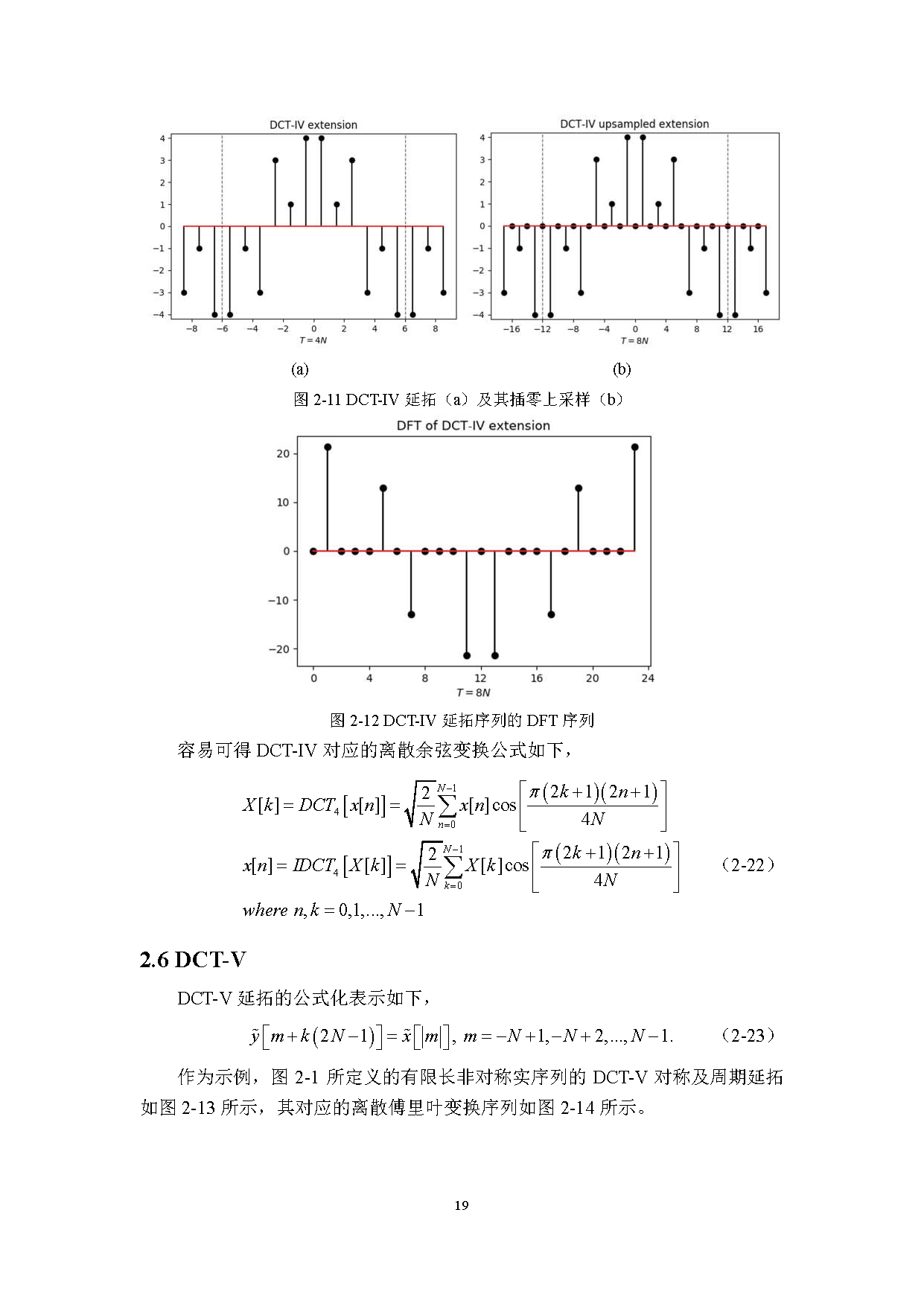
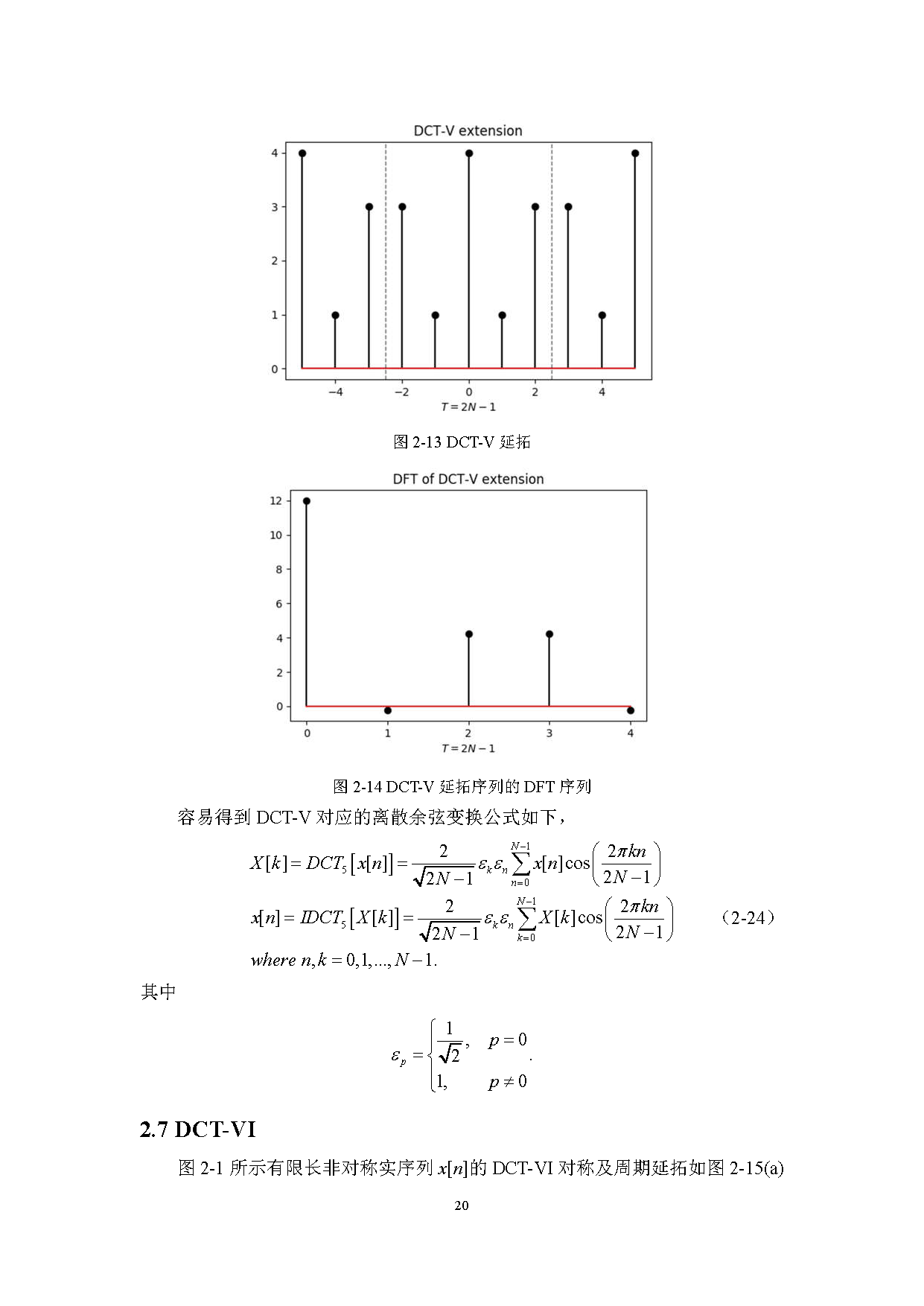
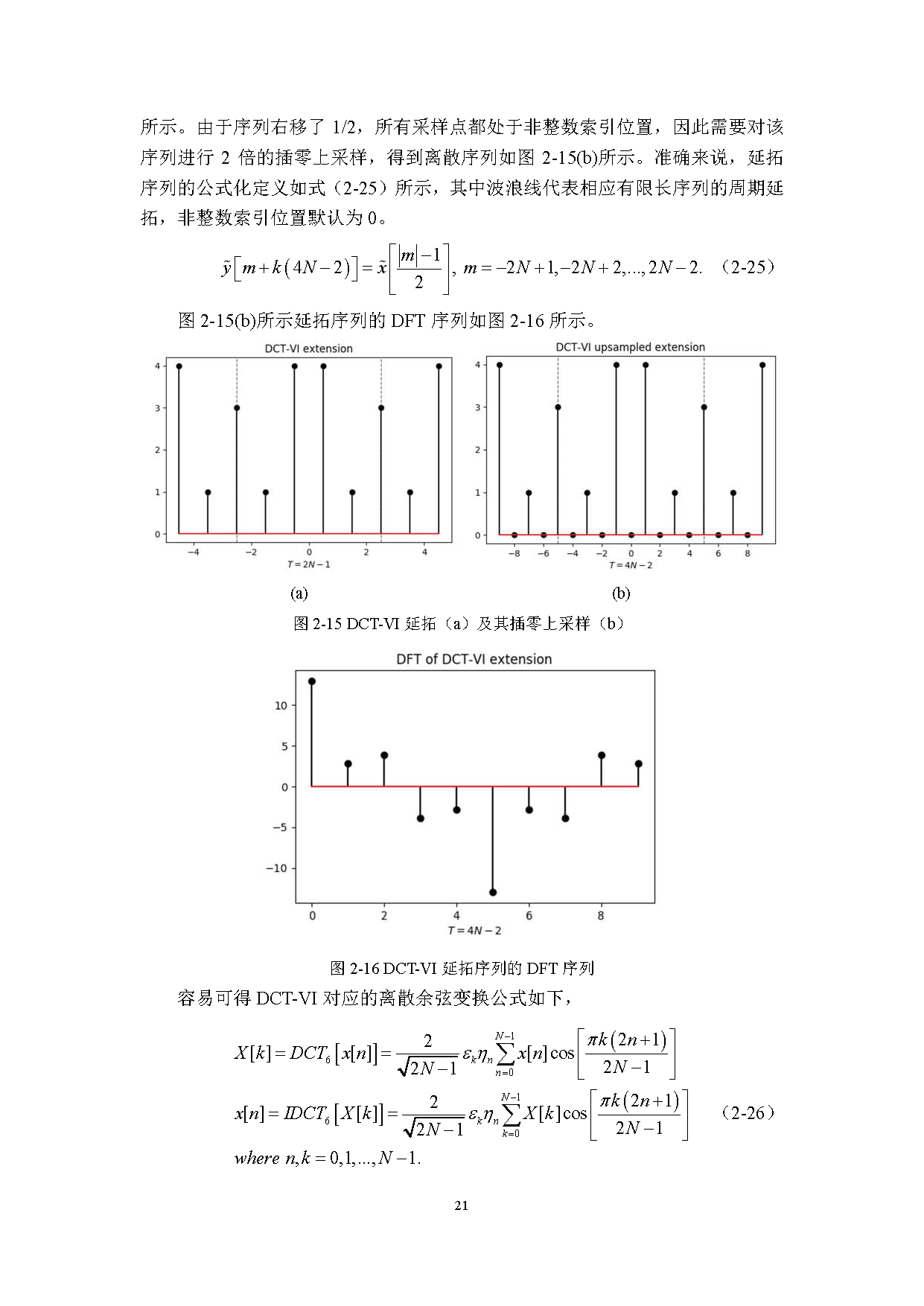
离散余弦变换







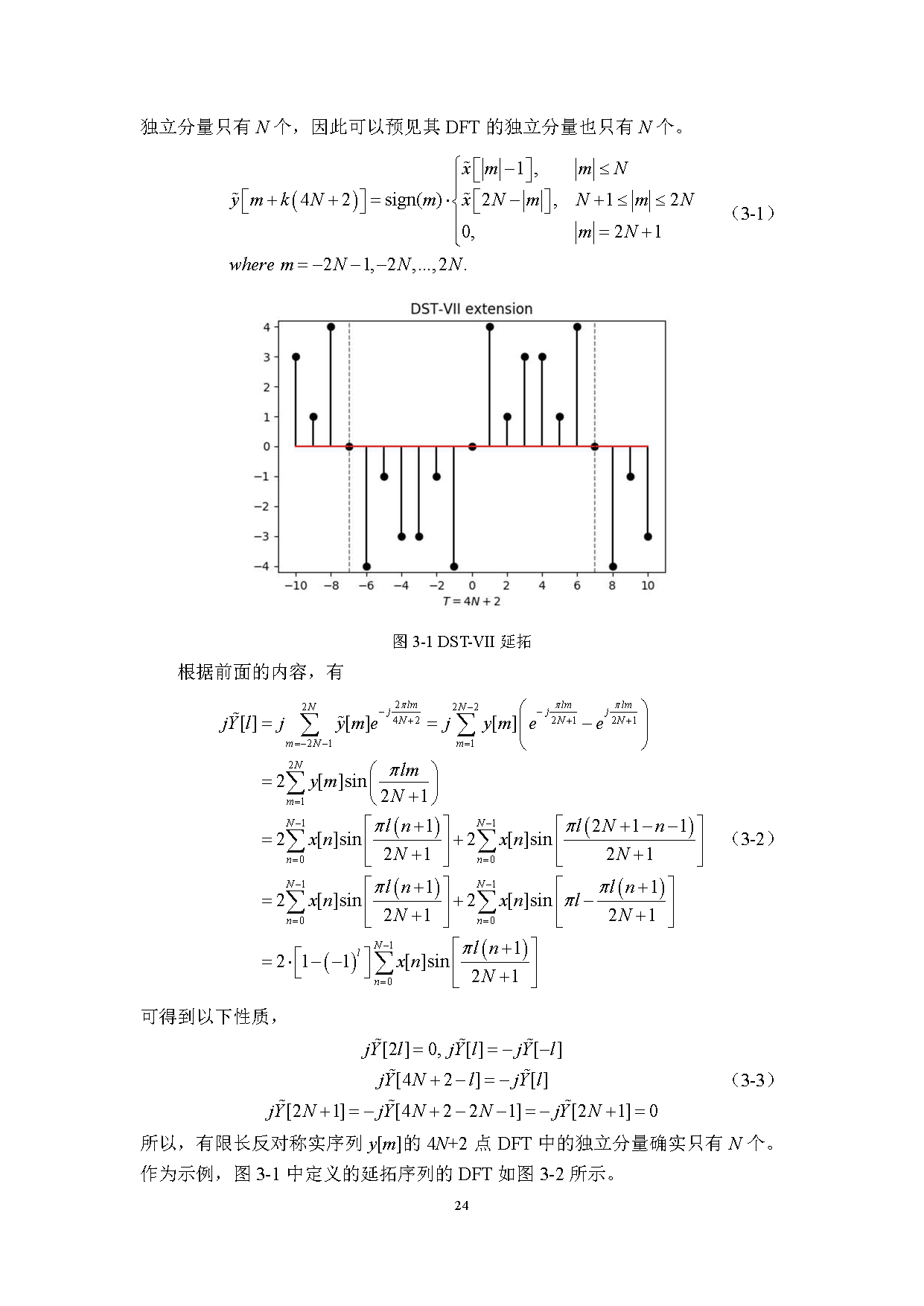
离散正弦变换


附录
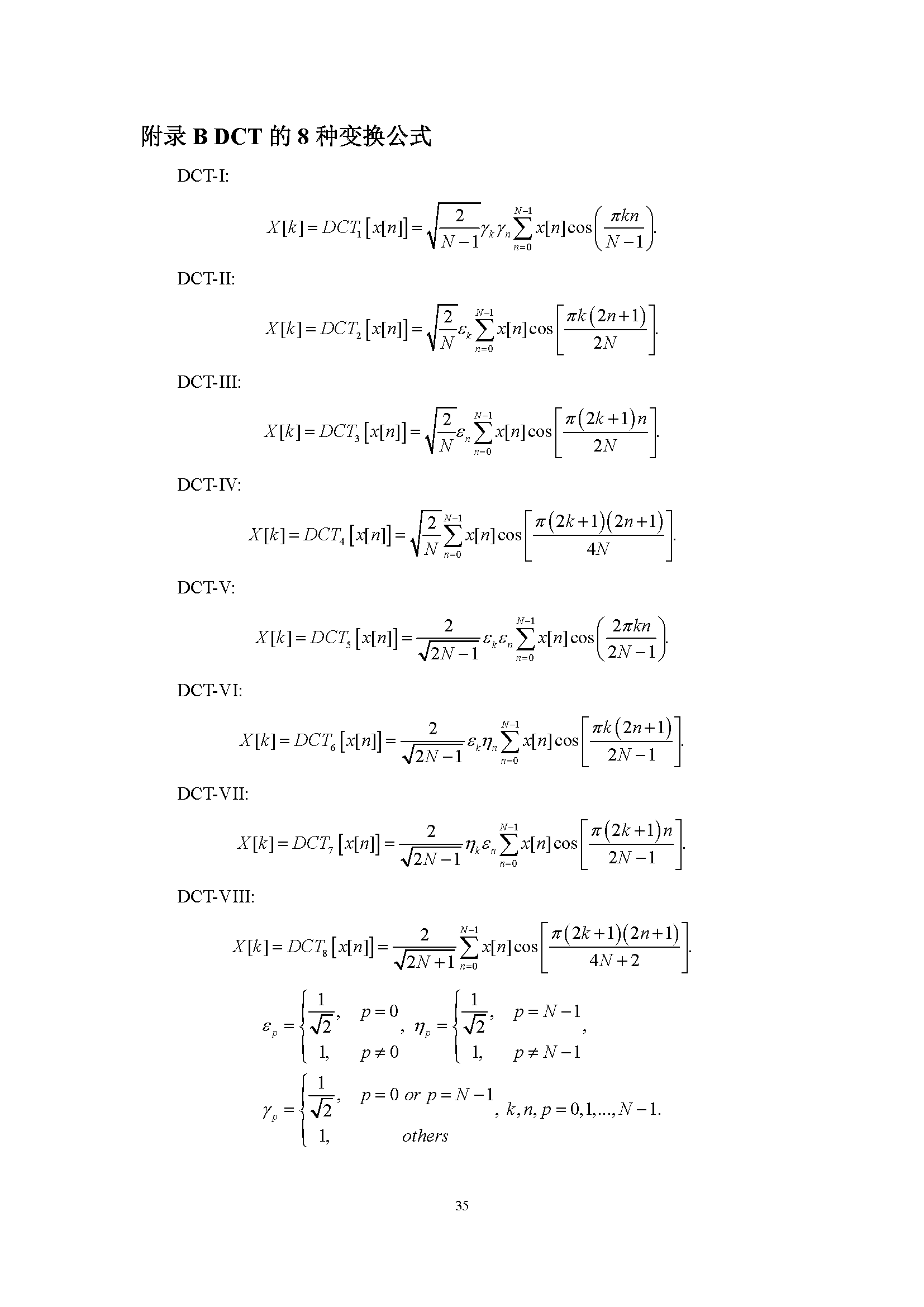
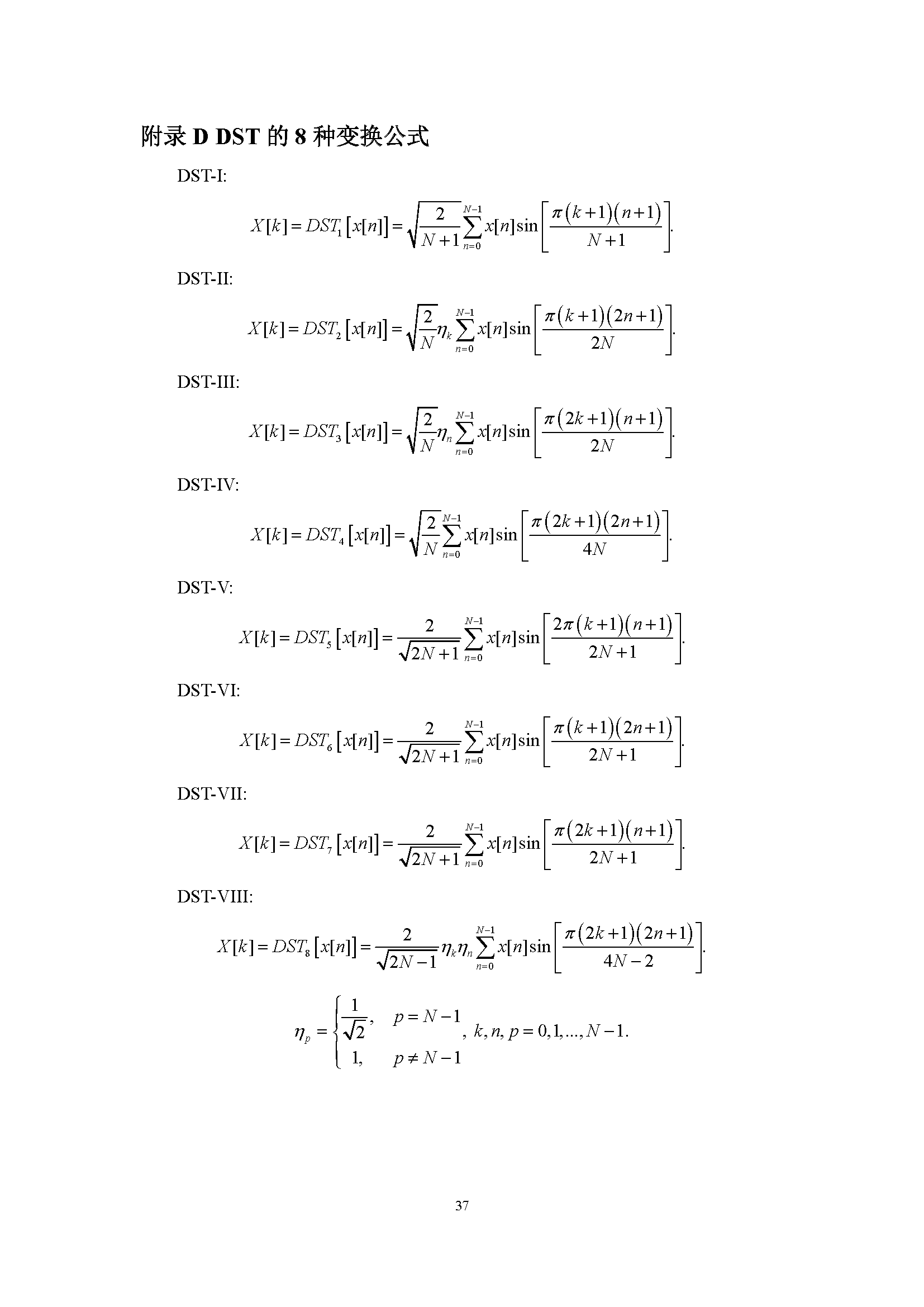
























 7661
7661











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








