问题背景
若某NPH问题q有多项式时间算法,则任一NP问题皆可多项式时间归约到q,故任一NP问题也是多项式时间可解的,由此可得NP=P. 传统时间复杂度中n表示数据输入的规模,如排序中n表示被排序的数据元素个数。但这不够严谨,其标准化的定义应该是:一个问题的输入规模是保存输入数据所需要的位数(bit),在此基础上定义的时间复杂度是标准的时间复杂度。
若一个算法的传统时间复杂度是多项式时间而其标准的时间复杂度不是多项式时间的,则该算法是伪多项式时间的。(例如朴素的素数判定算法), 一个具有伪多项式时间复杂度的NPC问题称为弱NPC问题,否则为强NPC问题
现实中许多优化问题是NP-hard的,由复杂性理论知:若P≠NP(并且很可能为真),就不可能找到多项式时间的算法来对问题的所有输入实例求出最优解。但若放松要求,就可能存在有效求解算法。
1.超多项式时间启发
不再要求多项式时间算法,有时求解问题存在超多项式时间算法,实用中相当快。例如,0/1背包问题是NPC问题,但存在1个伪多项式时间算法很容易解决它. 缺点:该技术只对少数问题有效(弱NPC问题)
2.启发式概率分析
不再要求问题的解满足所有的输入实例。在某些应用中,有可能输入实例的类被严格限制,对这些受限实例易于找到其有效算法。而这种结果往往归功于对输入实例约束的概率模型。缺点:选取一个特殊的输入分布往往是不易的。
3.近似算法
不再要求总是找到最优解。在实际应用中有时很难确定一个最优解和近似最优解(次优解)之间的差别,因问题的输入实例数据本身就可能是近似的。设计一个算法能够求出所有情况下的次优解来解NP-hard问题往往是真正有效的手段。
近似算法基本概念
优化问题近似解分类
1)容易近似
Knapsack,Scheduling,Bin Packing等
2)中等难度
Vertex Cover,Euclidean TSP,Steiner Trees等
3)难于近似 (这类问题即使找到很差的近似解也是NP-hard
Graph Coloring,TSP,Clique等
Def1 一个优化问题
∏
∏
∏由三部分构成:
实例集
D
D
D:输入实例的集合
解集
S
(
I
)
S(I)
S(I):输入实例
I
∊
D
I∊D
I∊D的所有可行解的集合
解的值函数
f
f
f:给每个解赋一个值,
f
:
S
(
I
)
→
R
f:S(I)→R
f:S(I)→R
Def2 若一个NPH判定问题 Π 1 Π_1 Π1是多项式可归约为计算一个优化问题 Π 2 Π_2 Π2的解,则 Π 2 Π_2 Π2是NPH的 。
Def3 一个近似算法A,是一个多项式时间求解优化问题 Π Π Π的算法,使得对一个给定的 Π Π Π的输入实例 I I I,它输出某个解 σ ∊ S ( I ) σ∊S(I) σ∊S(I)。通常,我们用 A ( I ) A(I) A(I)表示算法A所获得的解的值 f ( σ ) f(σ) f(σ)
近似算法的性能
算法质量(measure of goodness)是在最优解和近似解之间建立某种关系,这种度量也称为性能保证(Performance guarantees)。
最大值优化问题
∏
∏
∏是:
对于给定的I∊D,找一个解
σ
o
p
t
I
∈
S
(
I
)
\sigma_{opt}^I \in S(I)
σoptI∈S(I)使得:
∀
σ
∈
S
(
I
)
,
f
(
σ
o
p
t
I
)
≥
f
(
σ
)
\forall \sigma \in S(I), f(\sigma_{opt}^I) \geq f(\sigma)
∀σ∈S(I),f(σoptI)≥f(σ)
可以称为最优解的值
O
P
T
(
I
)
≜
f
(
σ
o
p
t
I
)
O P T(I) \triangleq f\left(\sigma_{o p t}^{I}\right)
OPT(I)≜f(σoptI)
装箱问题(BP)
非形式地,给定一个size在0,1之间的项的集合,要求将其放入单位size的箱子中,使得所用的箱子数目最少。故有最小优化问题:
- 实例: I = { s 1 , s 2 , … , s n } I=\{s_1, s_2, … , s_n\} I={s1,s2,…,sn}, 满足 ∀ i , s i ∈ [ 0 , 1 ] ∀i, s_i∈[0,1] ∀i,si∈[0,1]
- 解: σ = { B 1 , B 2 , … , B k } σ=\{B_1, B_2, … ,B_k\} σ={B1,B2,…,Bk}是 I 的一个不相交的划分,使得 ∀ i , B i ⊂ I ∀i, B_i⊂I ∀i,Bi⊂I 且 ∑ j ∈ B i s j ≤ 1 \sum_{j \in B_i}s_j \leq 1 ∑j∈Bisj≤1 (说明任一箱子中所装的所有物品size之和不超过1
- 解的值:使用的箱子数,即f(σ)=│σ│=k
在可行的时间内,求装箱问题的最优解是不可能的,但可求次最优解. 显然,比最优解多使用1个箱子的解是次最优的。一般地,我们希望找到1个近似解,其值与最优解的值相差某一小的常数.
Def4 绝对性能度量: 一个绝对近似算法是优化问题
Π
Π
Π的多项式时间近似算法A,使得对某一常数
k
>
0
k>0
k>0 满足:
∀
I
∈
D
,
∣
A
(
I
)
−
O
P
T
(
I
)
∣
≤
k
∀I∈D,|A(I)-OPT(I)| ≤ k
∀I∈D,∣A(I)−OPT(I)∣≤k. 这里
k
k
k也称为算法A的绝对误差.
(显然, 我们期望对任何NP-hard问题都有一个绝对近似算法,但是对于大多数NP-hard问题,仅当P=NP时,才能找到绝对近似算法(多项式时间), 但是P=NP时近似算法就没用了, 所以绝对近似算法也只能解决部分问题
绝对近似算法
图的顶点着色
使用最少的颜色数来为图G的顶点上色,使得所有相邻的顶点均有不同的颜色,即使G是平面图,该问题的判定版本也是NP-hard的,但它有1个绝对近似算法.
近似算法 A ( G ) A(G) A(G) { // 对任意平面图G染色
- 检验G是否可2染色(即判断G是否为二部图), 若是则G可2染色;
- 否则, 计算5染色; //可在多项式时间内, 任何平面图G是可5染色的 (实际上四色定理告诉我们G是可4染色的)
} // 这就证明了算法A比最优解多用的颜色数不会超过2
Th1:判定一个平面图是否可3着色的问题是NPC的
Th2:对给定的任意平面图G,近似算法A的性能满足:
∣
A
(
G
)
−
O
P
T
(
G
)
∣
≤
2
|A(G)-OPT(G)| ≤ 2
∣A(G)−OPT(G)∣≤2
图的边着色
使用最少的颜色为图的边上色,使得所有相邻的边有不同的颜色
Th3 Vizing定理:任一图至少需要Δ,至多需要Δ+1种颜色为边着色
Vizing定理的证明给出了一个多项式时间的算法A找到Δ+1边着色,但令人惊奇的是边着色问题即使是很特殊的情况也是NP-hard的
Th4 Holyer定理:确定一个3正则平面图所需的边着色数问题是NPH的 (正则图是每个顶点都有相同数目的邻居的图,即每个顶点的度相同。若每个顶点的度均为k,称为 k-正则图。
Th5:近似算法
A
A
A有性能保证:
∣
A
(
G
)
−
O
P
T
(
G
)
∣
≤
1
|A(G)-OPT(G)| ≤ 1
∣A(G)−OPT(G)∣≤1
小结
这两个例子似乎说明只有很特殊的一类优化问题可能有绝对近似算法:已知最优解的值或值所在的小范围。但最优解的值不易确定时是否有绝对近似算法仍然是未解决的问题.
所以对于研究近似算法的研究者而言, 为了避免做无用功, 在寻找目标问题的绝对近似算法之前, 应该先尝试判断目标绝对近似算法的存在性. 于是引入绝对近似算法的否定问题: 证明问题的绝对近似算法不存在.
0/1背包问题
项 集:
I
=
{
1
,
2
,
…
,
n
}
I=\{1,2,…,n\}
I={1,2,…,n}
大 小:
s
1
,
s
2
,
…
,
s
n
s_1,s_2,…,s_n
s1,s2,…,sn
利 润:
p
1
,
p
2
,
…
,
p
n
p_1,p_2,…,p_n
p1,p2,…,pn
背包容量:
B
B
B
问题的一个可行解是子集
I
’
⊆
I
,
∑
i
∈
I
′
s
i
≤
B
I’⊆I,\sum_{i \in I'} s_{i} \leq B
I’⊆I,∑i∈I′si≤B, 问题的最优解是使得
f
(
I
′
)
=
∑
i
∈
I
′
p
i
f\left(\mathbf{I}^{\prime}\right)=\sum_{i \in I^{\prime}} p_{i}
f(I′)=∑i∈I′pi最大化的可行解
0/1背包问题是NP-hard的,除非存在多项式时间算法能够找到最优解,否则不存在绝对近似算法
Th6 若
P
≠
N
P
P≠NP
P=NP,则对任何确定的k,找不到近似算法A可解背包问题使得:
∣
A
(
I
)
−
O
P
T
(
I
)
∣
≤
k
|A(I)-OPT(I)| ≤ k
∣A(I)−OPT(I)∣≤k
证明: 使用扩放法反证。 假定存在算法A具有性能保证k(k是正整数
设
∀
I
∊
D
∀I∊D
∀I∊D,可构造新实例
I
’
I’
I’使得
s
i
’
=
s
i
,
p
i
’
=
(
k
+
1
)
p
i
,
f
o
r
i
∊
[
1
,
n
]
s_i’=s_i,\ p_i’=(k+1)p_i,\ for \ i∊[1,n]
si’=si, pi’=(k+1)pi, for i∊[1,n]
即:除了利润扩放
k
+
1
k+1
k+1倍之外,其余参数不变。故
I
I
I的可行解也是
I
’
I’
I’的可行解,反之亦然。只是解的值相差
k
+
1
k+1
k+1 倍。
在
I
’
I’
I’上运行算法A获得解
A
(
I
’
)
A(I’)
A(I’),设A在实例
I
I
I上的解是
σ
σ
σ:
∣
A
(
I
’
)
−
O
P
T
(
I
’
)
∣
≤
k
⇒
∣
(
k
+
1
)
f
(
σ
)
−
(
k
+
1
)
O
P
T
(
I
)
∣
≤
k
⇒
∣
f
(
σ
)
−
O
P
T
(
I
)
∣
≤
k
/
(
k
+
1
)
⇒
∣
f
(
σ
)
−
O
P
T
(
I
)
∣
=
0
|A(I’)-OPT(I’)| ≤ k ⇒ | (k+1)f(σ)-(k+1)OPT(I)| ≤ k ⇒ |f(σ)-OPT(I)| ≤ k/(k+1) ⇒ |f(σ)-OPT(I)|=0
∣A(I’)−OPT(I’)∣≤k⇒∣(k+1)f(σ)−(k+1)OPT(I)∣≤k⇒∣f(σ)−OPT(I)∣≤k/(k+1)⇒∣f(σ)−OPT(I)∣=0
说明我们的绝对近似算法找到了问题的最优解, 那么这个多项式时间算法解决了NPH问题, 则
P
=
N
P
P = NP
P=NP与前提矛盾, 所以不可能存在绝对近似算法求解0/1背包问题, 定理得证.
小结
这里的例子说明在纯组合问题上,依然可用scaling扩放性质, 那么对于非数字问题是否可以继续使用scaling性质, 下面在团问题中讨论
团(Clique)问题
找图G中最大团(最大完全子图),该问题是NP-hard的 (顶点集C被称为无向图 G=(V,E) 的团,如果C是顶点集V的子集(C⊆V),而且任意两个C中的顶点都有边连接。即C中顶点及其连接这些顶点的边构成的子图是完全图 。极大团是指增加任一顶点都不再符合团定义的团,即极大团不能被任何一个更大的团所包含.
最大团是一个图中顶点数最多的团。图G的团数(clique number)ω(G) 是指G中最大团的顶点数。图G的边团覆盖数(edge clique cover number)是指覆盖G中所有的边所需要的最少的团的数目。图G的二分维数(bipartite dimension)是指覆盖G中所有边所需要的最少的二分团的数目,其中二分团(biclique)就是完全二 分子图 。而分团覆盖问题 (Clique cover problem)所关心的是用最少的团去覆盖G中所有的顶点。
独立集(independent set)是刚好和团相反的概念,因为图G中的团和图G的补图中的独立集是一一对应的。
Th7 若
P
≠
N
P
P≠NP
P=NP,则对于团问题不存在绝对近似算法
定义图的m次幂
G
m
G^m
Gm:取G的m个拷贝,连接位于不同副本里的任意两顶点
比如下面
G
2
G^2
G2是
G
G
G的两份拷贝并且不同拷贝副本之间任意两点连通
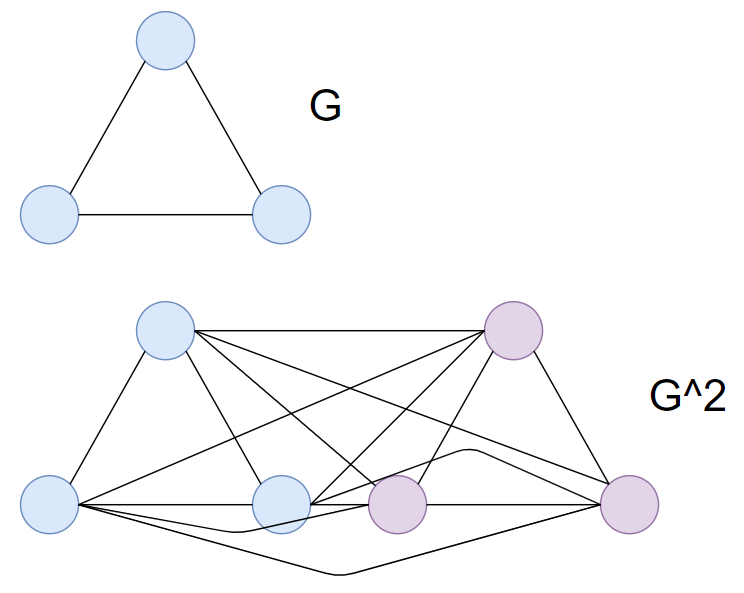
可证命题: G中最大团的size为α当且仅当Gm里最大团的size是mα
该命题直接给出了最优解之间的scaling性质:
O
P
T
(
G
K
+
1
)
=
(
k
+
1
)
O
P
T
(
G
)
OPT(G^{K+1})=(k+1)OPT(G)
OPT(GK+1)=(k+1)OPT(G)
Th7 证明
反证:设G是任意的无向图,近似算法A给出的绝对误差是k。在
G
k
+
1
G^{k+1}
Gk+1上运行A,若
G
G
G中最大团size为
α
α
α,则我们有
∣
A
(
G
k
+
1
)
−
O
P
T
(
G
k
+
1
)
∣
≤
k
⇒
∣
A
(
G
k
+
1
)
−
(
k
+
1
)
O
P
T
(
G
)
∣
≤
k
|A(G^{k+1})-OPT(G^{k+1})| ≤ k ⇒ |A(G^{k+1})-(k+1)OPT(G)| ≤ k
∣A(Gk+1)−OPT(Gk+1)∣≤k⇒∣A(Gk+1)−(k+1)OPT(G)∣≤k
对于任给的
G
m
G^m
Gm中体积为
β
β
β的团,易于用多项式时间在
G
G
G中找到一个体积为
β
/
m
β/m
β/m的团。因此我们能够在
G
G
G中找到一个团
C
C
C,使得
∣
A
(
G
k
+
1
)
−
(
k
+
1
)
O
P
T
(
G
)
∣
=
∣
(
k
+
1
)
∣
C
∣
−
(
k
+
1
)
O
P
T
(
G
)
∣
≤
k
⇒
∣
∣
C
∣
−
O
P
T
(
G
)
∣
≤
k
/
(
k
+
1
)
|A(G^{k+1})-(k+1)OPT(G)| = | (k+1)|C|-(k+1)OPT(G) | ≤ k \Rightarrow | |C|-OPT(G) | ≤ k/(k+1)
∣A(Gk+1)−(k+1)OPT(G)∣=∣(k+1)∣C∣−(k+1)OPT(G)∣≤k⇒∣∣C∣−OPT(G)∣≤k/(k+1)
因为
∣
C
∣
|C|
∣C∣和
O
P
T
(
G
)
OPT(G)
OPT(G)均是整数,故
A
(
G
)
=
∣
C
∣
A(G)=|C|
A(G)=∣C∣ 是最优团。即:多项式时间内找到了
G
G
G的最优解
A
(
G
)
A(G)
A(G). 则该绝对近似算法是多项式时间可解NPH问题的确定性算法, 则
P
=
N
P
P = NP
P=NP与前提矛盾, 命题得证.
总结
虽然我们渴望得到绝对性能保证,但是较难的优化问题很难找到绝对近似算法。因此,需要放松对“好的近似算法”的要求。所以除了绝对性能度量方法 (对某一常数 k > 0 k>0 k>0 满足: ∀ I ∈ D , ∣ A ( I ) − O P T ( I ) ∣ ≤ k ∀I∈D,|A(I)-OPT(I)| ≤ k ∀I∈D,∣A(I)−OPT(I)∣≤k) 之外, 还需要引入相对性能度量, 可见下篇: 多机调度问题








 本文探讨了NP问题与多项式时间算法的关联,指出若一个NPH问题有多项式时间算法,NP=P。同时,介绍了伪多项式时间算法和弱NPC问题。针对NP-hard问题,文章提出了三种求解策略:超多项式时间启发、启发式概率分析和近似算法,并详细解释了近似算法的性能度量,包括绝对性能度量和相对性能度量。通过0/1背包问题和团问题的例子,证明了在某些情况下不存在绝对近似算法。最后,讨论了寻找近似算法的重要性以及未来研究方向。
本文探讨了NP问题与多项式时间算法的关联,指出若一个NPH问题有多项式时间算法,NP=P。同时,介绍了伪多项式时间算法和弱NPC问题。针对NP-hard问题,文章提出了三种求解策略:超多项式时间启发、启发式概率分析和近似算法,并详细解释了近似算法的性能度量,包括绝对性能度量和相对性能度量。通过0/1背包问题和团问题的例子,证明了在某些情况下不存在绝对近似算法。最后,讨论了寻找近似算法的重要性以及未来研究方向。

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








