强化学习笔记(三)无模型预测(Model-Free Prediction)
动态规划法求解MDP时通过两个步骤进行迭代求解:状态评估和策略优化。也就是说我们面对一个动态的决策场景,首先需要对每个状态进行评估,然后走价值最好的路。价值函数一个深远的意义在于:它既包括即时奖励,又包括后续奖励的衰减和。这是一种顾全大局的Setting,如果只按Reward去贪婪选择的话,很可能出现“捡了芝麻,丢了西瓜”的事。因此只要价值函数是精确的,我们可以放心使用贪婪法去抉择。
上一节课我留有一个疑问,状态评估和策略优化这两个过程会相互影响吗?从Gridworld那个例子来看,我们的状态评估似乎并不受右边这列策略选择的影响。仔细看是我自己大意了,最初设定就说了是Random Policy,而右侧的Greedy Policy是在Random Policy的状态价值下选择的。因为只有终点的Reward是0,其余都是-1,所以状态价值肯定是趋向于终点方格的对称分布。而之后学习的Q-learning和Sarsa都是价值评估/策略选择相互影响的,其实单独看这个例子确实容易被误导。

动态规划是一种基于模型(Model-based)的方法,它要求每个状态转移概率已知。也就是我们以上帝视角去抉择,实际问题绝不会允许我们这么做。因此之后讨论的问题都是Model-Free的。很多书籍以方法分节,先讲蒙特卡洛法再讲时序差分法,我最近看Silver的UCL课程是以预测和控制两个角度分节的,所以我也按他的顺序去整理我的想法。
Q1:对修正公式的理解?为什么使用 α \alpha α因子比 1 / N ( S ) 1/N(S) 1/N(S)效果更好?使用计数器不是会更精准吗?
Silver在课堂上有所解释。
1.不需要保留一些数据,只需要递增的更新。也就是说不需要单独存储计数器。当然这肯定不是主要的原因。
2. 取一个完整的均值可能并不是最科学的方法,我们可能还没到过度正确的程度。
这听起来比较抽象,我的理解是使用
α
\alpha
α会更加灵活,可以自由设定步长。而
1
/
N
(
s
)
1/N(s)
1/N(s)并不一定有好的效果。这就像最优化方法里精确线搜索和非精确线搜索。
Q2:TD法比MC法效率更高、效果更好的原因?
- MC法必须等一个序列结束再回溯,而TD法只需往前看一步。
- TD法充分利用了Markov Properties,MC没有。贝尔曼方程就是马尔可夫性的体现。
- TD法的方差比较小,收敛快;MC法初期震荡大。
我的理解是:MC法是试探法,用大的频数去模拟频率,因此状态价值更多是以概率平均的形式体现;TD法更多考虑了相邻状态价值之间的关系,由课上的例子就可以看出。

在这个例子里,我们经历个8个序列,只有简单的A,B两个状态,得到的即时奖励跟在状态后面。首先,B的状态价值函数 V ( B ) V(B) V(B)好求,由于B在序列中永远是最后一个状态,所以只要取平均就好了, V ( B ) = R t = 6 / 8 V(B) = R_{t} = 6/8 V(B)=Rt=6/8. 而A只在第一个序列中出现过,如果我们用MC法求解的话, V ( A ) = R t + V(A) = R_{t}+ V(A)=Rt+ γ \gamma γ R t + 1 = 0 + 0 = 0 R_{t+1}=0+0=0 Rt+1=0+0=0. 如果用TD法求解的话, V ( A ) = R t + V(A) = R_{t}+ V(A)=Rt+ γ \gamma γ V B = 6 / 8 V_{B}=6/8 VB=6/8. 可以看到两种方法解出来结果不同。这里也不能说谁对谁错,但是明显TD法更是对MDP的精准描述。
Q3: T D TD TD( λ \lambda λ)为什么要用到几何加权而不是别的手段?
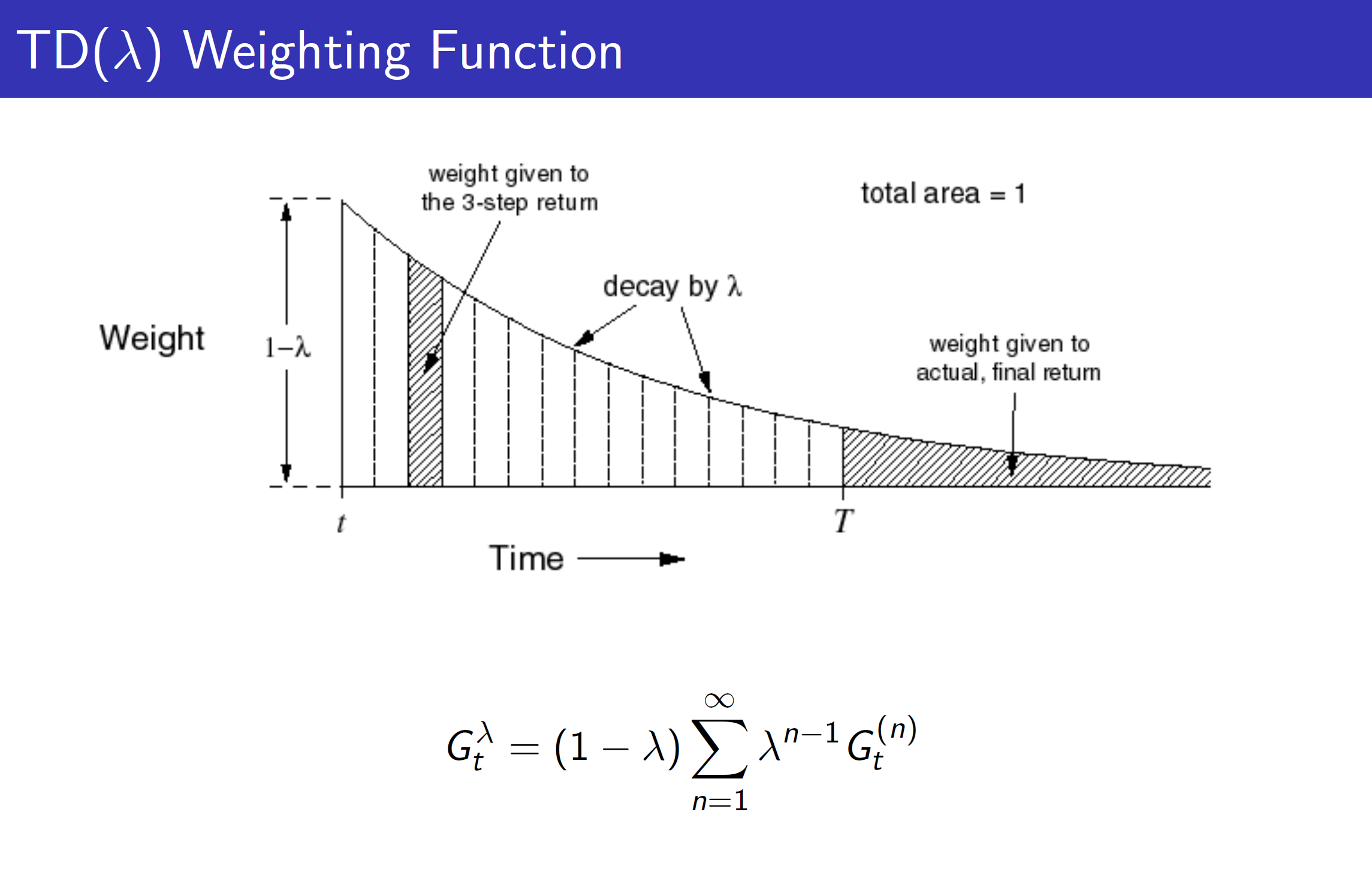
首先, T D TD TD( λ \lambda λ)是一种广义的描述。课上刚好有学生提出了这个问题,老师的回答是:
- 便于高效计算。(数学上性质较好,根据等比数列求和公式,结果为1)
- 这是memory-less的公式,也就是说我们不用存储于时间相关的系数。我的理解是,当前时刻的权重越大,往后的会逐次衰减,有点类似于我们定义收益Gain的式子。
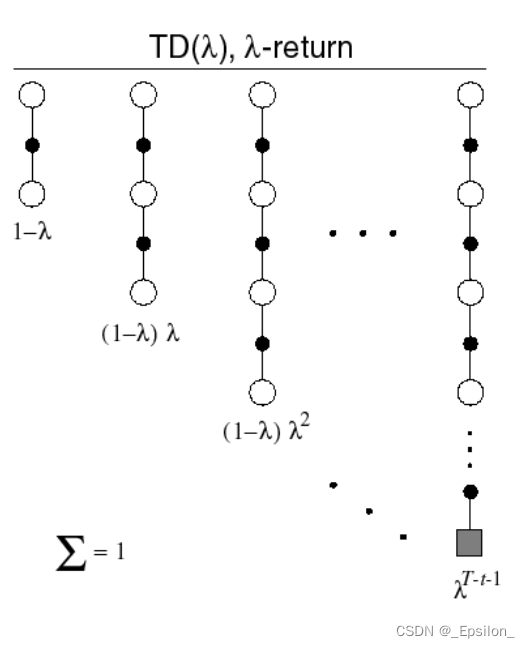
Q4:为什么 λ = 0 \lambda=0 λ=0变成时序差分法, λ = 1 \lambda=1 λ=1变成蒙特卡洛法?
这个跟数学公式有关。
(
1
−
λ
)
∑
n
=
1
∞
λ
n
−
1
G
t
(
n
)
=
(
1
−
λ
)
G
t
(
1
)
+
(
1
−
λ
)
λ
G
t
(
2
)
+
.
.
.
(1-\lambda) \sum_{n=1}^{\infty} \lambda^{n-1} G_{t}^{(n)}=(1-\lambda)G_{t}^{(1)}+(1-\lambda)\lambda G_{t}^{(2)}+...
(1−λ)n=1∑∞λn−1Gt(n)=(1−λ)Gt(1)+(1−λ)λGt(2)+...
G
t
(
n
)
=
R
t
+
1
+
γ
R
t
+
2
+
…
+
γ
n
−
1
R
t
+
n
+
γ
n
V
(
S
t
+
n
)
G_{t}^{(n)}=R_{t+1}+\gamma R_{t+2}+\ldots+\gamma^{n-1} R_{t+n}+\gamma^{n} V\left(S_{t+n}\right)
Gt(n)=Rt+1+γRt+2+…+γn−1Rt+n+γnV(St+n) 当
λ
=
0
\lambda=0
λ=0的时候,公式变为
G
t
(
1
)
G_{t}^{(1)}
Gt(1),就是普通的时序差分法。
当
λ
=
1
\lambda=1
λ=1的时候,原式不能仅仅因为
1
−
λ
=
0
1-\lambda=0
1−λ=0而看作0. 它是无穷大个无穷小构成,应该看成等比级数求和。我们假设由于n趋于无穷,所以基本所有步骤的收获都是
G
t
(
n
)
G_{t}^{(n)}
Gt(n),求和的部分也就是
∑
n
=
1
∞
λ
n
−
1
=
1
−
λ
n
\sum_{n=1}^{\infty} \lambda^{n-1}=1-\lambda^{n}
∑n=1∞λn−1=1−λn. 这样这个等比级数的和是
(
1
−
λ
n
)
G
t
(
n
)
\left(1-\lambda^{n}\right) G_{t}^{(n)}
(1−λn)Gt(n),当n趋于无穷时,最终得出
G
t
(
n
)
G_{t}^{(n)}
Gt(n),这就是蒙特卡洛法.
Q5:Forward View, Backward View, 资格迹
这一块是我觉得最难理解的地方了。首先提出了n步时序差分,这是Q3,Q4里讲到的,这为更加广义地描述方法。之后又提出
T
D
TD
TD(
λ
\lambda
λ)的
λ
\lambda
λ收获:n从1到
∞
\infty
∞所有步的收获乘以权重的和。这样就把所有步的收获都考虑进来了,这是前向看
T
D
TD
TD(
λ
\lambda
λ).
从反向来看,引入了资格迹(Eligibility, E)的概念。用一步差分作为误差,然后乘以资格迹,在推导上与前向公式
G
t
λ
−
V
(
S
t
)
G_{t}^{\lambda}-V\left(S_{t}\right)
Gtλ−V(St)是一样的,这里可以看刘老师的这篇博客,推导得十分详细。
资格迹的公式:
E
0
(
s
)
=
0
E_{0}(s)=0
E0(s)=0
E
t
(
s
)
=
γ
λ
E
t
−
1
(
s
)
+
1
(
S
t
=
s
)
=
{
0
t
<
k
(
γ
λ
)
t
−
k
t
≥
k
,
s.t.
λ
,
γ
∈
[
0
,
1
]
,
s
is visited once at time
k
E_{t}(s)=\gamma \lambda E_{t-1}(s)+1\left(S_{t}=s\right)=\left\{\begin{array}{ll} 0 & t<k \\ (\gamma \lambda)^{t-k} & t \geq k \end{array}, \quad \text { s.t. } \lambda, \gamma \in[0,1], s \text { is visited once at time } k\right.
Et(s)=γλEt−1(s)+1(St=s)={0(γλ)t−kt<kt≥k, s.t. λ,γ∈[0,1],s is visited once at time k
从公式形式上来分析,资格迹是包含两个参数的指数衰减,这与几何级数的
T
D
TD
TD(
λ
\lambda
λ)有一些相似,也印证了二者是相同表达的结果。
至于说它是怎么应用的,有什么深层次的含义,我还不明白。目前只是知其然而不知其所以然~希望后续我能填上这个坑
V
(
S
t
)
=
V
(
S
t
)
+
α
(
G
t
λ
−
V
(
S
t
)
)
δ
t
=
R
t
+
1
+
γ
v
(
S
t
+
1
)
−
V
(
S
t
)
V
(
S
t
)
=
V
(
S
t
)
+
α
δ
t
E
t
(
s
)
\begin{gathered} V\left(S_t\right)=V\left(S_t\right)+\alpha\left(G_t^\lambda-V\left(S_t\right)\right)\\\\ \delta_t=R_{t+1}+\gamma v\left(S_{t+1}\right)-V\left(S_t\right) \\ V\left(S_t\right)=V\left(S_t\right)+\alpha \delta_t E_t(s) \end{gathered}
V(St)=V(St)+α(Gtλ−V(St))δt=Rt+1+γv(St+1)−V(St)V(St)=V(St)+αδtEt(s)
也就是说一步差分乘以资格迹与
λ
\lambda
λ收获做差分是相同效果。后续收获的衰减和都可以包含在资格迹中。
G t λ − V ( S t ) = − V ( S t ) + ( 1 − λ ) λ 0 ( R t + 1 + γ V ( S t + 1 ) ) + ( 1 − λ ) λ 1 ( R t + 1 + γ R t + 2 + γ 2 V ( S t + 2 ) ) + ( 1 − λ ) λ 2 ( R t + 1 + γ R t + 2 + γ 2 R t + 3 + γ 3 V ( S t + 3 ) ) + … = − V ( S t ) + ( γ λ ) 0 ( R t + 1 + γ V ( S t + 1 ) − γ λ V ( S t + 1 ) ) + ( γ λ ) 1 ( R t + 2 + γ V ( S t + 2 ) − γ λ V ( S t + 2 ) ) + ( γ λ ) 2 ( R t + 3 + γ V ( S t + 3 ) − γ λ V ( S t + 3 ) ) + … = ( γ λ ) 0 ( R t + 1 + γ V ( S t + 1 ) − V ( S t ) ) + ( γ λ ) 1 ( R t + 2 + γ V ( S t + 2 ) − V ( S t + 1 ) ) + ( γ λ ) 2 ( R t + 3 + γ V ( S t + 3 ) − V ( S t + 2 ) ) + … = δ t + γ λ δ t + 1 + ( γ λ ) 2 δ t + 2 + … \begin{aligned} G_t^\lambda-V\left(S_t\right) & =-V\left(S_t\right)+(1-\lambda) \lambda^0\left(R_{t+1}+\gamma V\left(S_{t+1}\right)\right) \\ & +(1-\lambda) \lambda^1\left(R_{t+1}+\gamma R_{t+2}+\gamma^2 V\left(S_{t+2}\right)\right) \\ & +(1-\lambda) \lambda^2\left(R_{t+1}+\gamma R_{t+2}+\gamma^2 R_{t+3}+\gamma^3 V\left(S_{t+3}\right)\right) \\ & +\ldots \\ & =-V\left(S_t\right)+(\gamma \lambda)^0\left(R_{t+1}+\gamma V\left(S_{t+1}\right)-\gamma \lambda V\left(S_{t+1}\right)\right) \\ & +(\gamma \lambda)^1\left(R_{t+2}+\gamma V\left(S_{t+2}\right)-\gamma \lambda V\left(S_{t+2}\right)\right) \\ & +(\gamma \lambda)^2\left(R_{t+3}+\gamma V\left(S_{t+3}\right)-\gamma \lambda V\left(S_{t+3}\right)\right) \\ & +\ldots \\ & =(\gamma \lambda)^0\left(R_{t+1}+\gamma V\left(S_{t+1}\right)-V\left(S_t\right)\right) \\ & +(\gamma \lambda)^1\left(R_{t+2}+\gamma V\left(S_{t+2}\right)-V\left(S_{t+1}\right)\right) \\ & +(\gamma \lambda)^2\left(R_{t+3}+\gamma V\left(S_{t+3}\right)-V\left(S_{t+2}\right)\right) \\ & +\ldots \\ & =\delta_t+\gamma \lambda \delta_{t+1}+(\gamma \lambda)^2 \delta_{t+2}+\ldots \end{aligned} Gtλ−V(St)=−V(St)+(1−λ)λ0(Rt+1+γV(St+1))+(1−λ)λ1(Rt+1+γRt+2+γ2V(St+2))+(1−λ)λ2(Rt+1+γRt+2+γ2Rt+3+γ3V(St+3))+…=−V(St)+(γλ)0(Rt+1+γV(St+1)−γλV(St+1))+(γλ)1(Rt+2+γV(St+2)−γλV(St+2))+(γλ)2(Rt+3+γV(St+3)−γλV(St+3))+…=(γλ)0(Rt+1+γV(St+1)−V(St))+(γλ)1(Rt+2+γV(St+2)−V(St+1))+(γλ)2(Rt+3+γV(St+3)−V(St+2))+…=δt+γλδt+1+(γλ)2δt+2+…

























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








